Chapter 4.3, Problem 26E

Imports and exports: The following table presents the U.S. imports and exports (in billions of dollars) for each of 29 months.

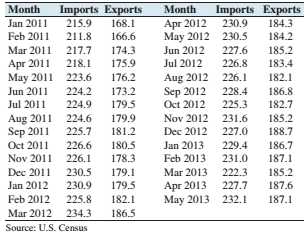
1. Compute the least-squares regression line for predicting exports (y) from imports (x).
2. Compute the coefficient of determination.
3. The months with the two lowest exports are January and February 2011 Remove these points and compute the least-squares regression line. Is the result noticeably different?
4. Compute the coefficient of determination for the data set with January and February 2011 removed.
5. Two economists decide to study the relationship between imports and exports. One uses data from January 2011 through May 2013 and the other used data from March 2011 through May 2013. For which data set will the proportion of variance explained by the least-squares regression line be greater?

To determine

The least squares regression line for the given data set.

Answer to Problem 26E

$y=0.8868x-19.2390$

Explanation of Solution

Given information:

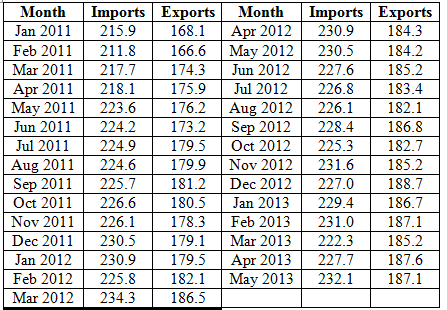
The following table presents the U.S. imports and exports (in billions of dollars) for each of $29$

months:

Concepts Used:

The equation for least-square regression line:

$y=b_0+b_{1}x$

Where $b_1=r\frac{s_y}{s_x}$ is the slope and $b_0=\overline{y}-b_1\overline{x}$ is the $y$ -intercept.

The correlation coefficient of a data is given by:

$r=\frac{1}{n}\frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{s_x{s}_y}$

Where,

$\overline{x},\overline{y}$ represent the mean of $x$ and $y$ respectively. $s_x,s_y$ represent the standard deviations of $x$ and $y$, $n$ represents the number of terms.

The standard deviations are given by:

$s_x=\sqrt{\frac{{\displaystyle \sum {\left(x-\overline{x}\right)}^2}}{n}},s_y=\sqrt{\frac{{\displaystyle \sum {\left(y-\overline{y}\right)}^2}}{n}}$

Calculation:

The mean of $x$ is given by:

$\begin{array}{l}\overline{x}=\frac{{\displaystyle \sum x}}{n}=\frac{\begin{array}{l}215.9+211.8+217.7+218.1+223.6+224.2+224.9+224.6+225.7+226.6+226.1+230.5+\\ 230.9+225.8+234.3+230.9+230.5+227.6+226.8+226.1+228.4+225.3+231.6+227.0+\\ 229.4+231+222.3+227.7+232.1\end{array}}{29}\\ \overline{x}=\frac{{\displaystyle \sum x}}{n}=\frac{6557.4}{29}=226.11724\end{array}$

The mean of $y$ is given by:

$\begin{array}{l}\overline{y}=\frac{{\displaystyle \sum y}}{n}=\frac{\begin{array}{l}168.1+166.6+174.3+175.9+176.2+173.2+179.5+179.9+181.2+180.5+178.3+179.1+\\ 179.5+182.1+186.5+184.3+184.2+185.2+183.4+182.1+186.8+182.7+185.2+188.7+\\ 186.7+187.1+185.2+187.6+187.1\end{array}}{29}\\ \overline{y}=\frac{{\displaystyle \sum y}}{n}=\frac{5257.2}{29}=181.28276\end{array}$

The data can be represented in tabular form as:

x	y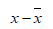
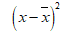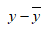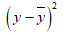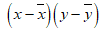215.9	168.1	-10.21724	104.39202	-13.18276	173.78512	134.69143
211.8	166.6	-14.31724	204.98340	-14.68276	215.58340	210.21660
217.7	174.3	-8.41724	70.84995	-6.98276	48.75892	58.77556
218.1	175.9	-8.01724	64.27616	-5.38276	28.97409	43.15488
223.6	176.2	-2.51724	6.33650	-5.08276	25.83444	12.79453
224.2	173.2	-1.91724	3.67581	-8.08276	65.33099	15.49660
224.9	179.5	-1.21724	1.48168	-1.78276	3.17823	2.17005
224.6	179.9	-1.51724	2.30202	-1.38276	1.91202	2.09798
225.7	181.2	-0.41724	0.17409	-0.08276	0.00685	0.03453
226.6	180.5	0.48276	0.23306	-0.78276	0.61271	-0.37788
226.1	178.3	-0.01724	0.00030	-2.98276	8.89685	0.05143
230.5	179.1	4.38276	19.20857	-2.18276	4.76444	-9.56650
230.9	179.5	4.78276	22.87478	-1.78276	3.17823	-8.52650
225.8	182.1	-0.31724	0.10064	0.81724	0.66788	-0.25926
234.3	186.5	8.18276	66.95754	5.21724	27.21961	42.69143
230.9	184.3	4.78276	22.87478	3.01724	9.10375	14.43074
230.5	184.2	4.38276	19.20857	2.91724	8.51030	12.78556
227.6	185.2	1.48276	2.19857	3.91724	15.34478	5.80832
226.8	183.4	0.68276	0.46616	2.11724	4.48271	1.44556
226.1	182.1	-0.01724	0.00030	0.81724	0.66788	-0.01409
228.4	186.8	2.28276	5.21099	5.51724	30.43995	12.59453
225.3	182.7	-0.81724	0.66788	1.41724	2.00857	-1.15823
231.6	185.2	5.48276	30.06064	3.91724	15.34478	21.47729
227.0	188.7	0.88276	0.77926	7.41724	55.01547	6.54763
229.4	186.7	3.28276	10.77650	5.41724	29.34650	17.78350
231.0	187.1	4.88276	23.84133	5.81724	33.84030	28.40419
222.3	185.2	-3.81724	14.57133	3.91724	15.34478	-14.95306
227.7	187.6	1.58276	2.50512	6.31724	39.90754	9.99867
232.1	187.1	5.98276	35.79340	5.81724	33.84030	34.80315
$\overline{x}=226.11724$	$\overline{y}=181.28276$		$\begin{array}{l}{\displaystyle \sum {\left(x-\overline{x}\right)}^2}=\\ 736.80138\end{array}$		$\begin{array}{l}{\displaystyle \sum {\left(y-\overline{y}\right)}^2}=\\ 901.90138\end{array}$	$\begin{array}{l}{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}\\ =653.39862\end{array}$

Hence, the standard deviation is given by:

$\begin{array}{l}{s}_x=\sqrt{\frac{{\displaystyle \sum {\left(x-\overline{x}\right)}^2}}{n}}\\ s_x=\sqrt{\frac{736.80138}{29}}\\ s_x=\sqrt{25.40694}\end{array}$

And,

$\begin{array}{l}{s}_y=\sqrt{\frac{{\displaystyle \sum {\left(y-\overline{y}\right)}^2}}{n}}\\ s_y=\sqrt{\frac{901.90138}{29}}\\ s_y=\sqrt{31.10005}\end{array}$

Consider, $r=\frac{1}{n}\frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{s_x{s}_y}$

Putting the values in the formula,

$\begin{array}{l}r=\frac{1}{n}\frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{s_x{s}_y}\\ r=\frac{1}{29}\cdot \frac{653.39862}{\left(\sqrt{25.40694}\right)\left(\sqrt{31.10005}\right)}\\ r=0.80154\end{array}$

Putting the values to obtain b₁,

$\begin{array}{l}{b}_1=r\frac{s_y}{s_x}\\ b_1=\frac{1}{29}\cdot \frac{653.39862}{\left(\sqrt{25.40694}\right)\left(\sqrt{31.10005}\right)}\frac{\left(\sqrt{31.10005}\right)}{\left(\sqrt{25.40694}\right)}\\ b_1=0.8868\end{array}$

Putting the values to obtain b₀,

$\begin{array}{l}{b}_0=\overline{y}-b_1\overline{x}\\ b_0=\left(181.28276\right)-\left(0.8868\right)\left(226.11724\right)\\ b_0=-19.2390\end{array}$

Hence, the least-square regression line is given by:

$\begin{array}{l}y=b_0+b_{1}x\\ y=\left(-19.2390\right)+\left(0.8868\right)x\\ y=0.8868x-19.2390\end{array}$

Therefore, the least squares regression line for the given data set is $y=0.8868x-19.2390$

To determine

The coefficient of determination.

Answer to Problem 26E

$0.89529$.

Explanation of Solution

Given information:

Same as part $a$.

Calculation:

From part $a$ of this exercise, the correlation coefficient is $r=0.80154$

The coefficient of determination is given by:

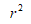
Where $r$ is the correlation coefficient of the data.

Putting the values to obtain Coefficient of Determination,

$r^2={\left(0.80154\right)}^2=0.8952876633\approx 0.89529$

Therefore, the Coefficient of Determination is $0.89529$.

To determine

The least squares regression line for the given data set by excluding the outlier points and to check if the result is noticeably different.

Answer to Problem 26E

$y=0.699x+23.6335$

The result is noticeably different.

Explanation of Solution

Given information:

Same as part $a$.

The months with two lowest exports are January and February $2011$.

Concepts used:

The equation for least-square regression line:

$y=b_0+b_{1}x$

Where $b_1=r\frac{s_y}{s_x}$ is the slope and $b_0=\overline{y}-b_1\overline{x}$ is the $y$ -intercept.

The correlation coefficient of a data is given by:

$r=\frac{1}{n}\frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{s_x{s}_y}$

Where,

$\overline{x},\overline{y}$ represent the mean of $x$ and $y$ respectively. $s_x,s_y$ represent the standard deviations of $x$ and $y$, $n$ represents the number of terms.

The standard deviations are given by:

$s_x=\sqrt{\frac{{\displaystyle \sum {\left(x-\overline{x}\right)}^2}}{n}},s_y=\sqrt{\frac{{\displaystyle \sum {\left(y-\overline{y}\right)}^2}}{n}}$

Calculation:

The months with two lowest exports are January and February $2011$. So these points $(215.9,168.1)\text{ and }(211.8,166.6)$ should be excluded.

Excluding the outlier,

The mean of $x$ is given by:

$\begin{array}{l}\overline{x}=\frac{{\displaystyle \sum x}}{n}=\frac{\begin{array}{l}217.7+218.1+223.6+224.2+224.9+224.6+225.7+226.6+226.1+230.5+230.9+\\ 225.8+234.3+230.9+230.5+227.6+226.8+226.1+228.4+225.3+231.6+227.0+\\ 229.4+231+222.3+227.7+232.1\end{array}}{27}\\ \overline{x}=\frac{{\displaystyle \sum x}}{n}=\frac{6129.7}{27}=227.02593\end{array}$

The mean of $y$ is given by:

$\begin{array}{l}\overline{y}=\frac{{\displaystyle \sum y}}{n}=\frac{\begin{array}{l}174.3+175.9+176.2+173.2+179.5+179.9+181.2+180.5+178.3+179.1+179.5+\\ 182.1+186.5+184.3+184.2+185.2+183.4+182.1+186.8+182.7+185.2+188.7+\\ 186.7+187.1+185.2+187.6+187.1\end{array}}{27}\\ \overline{y}=\frac{{\displaystyle \sum y}}{n}=\frac{4922.5}{27}=182.31481\end{array}$

The data can be represented in tabular form as:

x	y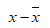
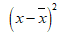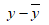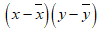217.7	174.3	-8.41724	70.84995	-6.98276	48.75892	58.77556
218.1	175.9	-8.01724	64.27616	-5.38276	28.97409	43.15488
223.6	176.2	-2.51724	6.33650	-5.08276	25.83444	12.79453
224.2	173.2	-1.91724	3.67581	-8.08276	65.33099	15.49660
224.9	179.5	-1.21724	1.48168	-1.78276	3.17823	2.17005
224.6	179.9	-1.51724	2.30202	-1.38276	1.91202	2.09798
225.7	181.2	-0.41724	0.17409	-0.08276	0.00685	0.03453
226.6	180.5	0.48276	0.23306	-0.78276	0.61271	-0.37788
226.1	178.3	-0.01724	0.00030	-2.98276	8.89685	0.05143
230.5	179.1	4.38276	19.20857	-2.18276	4.76444	-9.56650
230.9	179.5	4.78276	22.87478	-1.78276	3.17823	-8.52650
225.8	182.1	-0.31724	0.10064	0.81724	0.66788	-0.25926
234.3	186.5	8.18276	66.95754	5.21724	27.21961	42.69143
230.9	184.3	4.78276	22.87478	3.01724	9.10375	14.43074
230.5	184.2	4.38276	19.20857	2.91724	8.51030	12.78556
227.6	185.2	1.48276	2.19857	3.91724	15.34478	5.80832
226.8	183.4	0.68276	0.46616	2.11724	4.48271	1.44556
226.1	182.1	-0.01724	0.00030	0.81724	0.66788	-0.01409
228.4	186.8	2.28276	5.21099	5.51724	30.43995	12.59453
225.3	182.7	-0.81724	0.66788	1.41724	2.00857	-1.15823
231.6	185.2	5.48276	30.06064	3.91724	15.34478	21.47729
227.0	188.7	0.88276	0.77926	7.41724	55.01547	6.54763
229.4	186.7	3.28276	10.77650	5.41724	29.34650	17.78350
231.0	187.1	4.88276	23.84133	5.81724	33.84030	28.40419
222.3	185.2	-3.81724	14.57133	3.91724	15.34478	-14.95306
227.7	187.6	1.58276	2.50512	6.31724	39.90754	9.99867
232.1	187.1	5.98276	35.79340	5.81724	33.84030	34.80315
$\overline{x}=227.02593$	$\overline{y}=182.31481$		$\begin{array}{l}{\displaystyle \sum {\left(x-\overline{x}\right)}^2}\\ =405.13185\end{array}$		$\begin{array}{l}{\displaystyle \sum {\left(y-\overline{y}\right)}^2}\\ =483.77407\end{array}$	$\begin{array}{l}{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}\\ =283.16963\end{array}$

Hence, the standard deviation is given by:

$\begin{array}{l}{s}_x=\sqrt{\frac{{\displaystyle \sum {\left(x-\overline{x}\right)}^2}}{n}}\\ s_x=\sqrt{\frac{405.13185}{27}}\\ s_x=\sqrt{15.00488}\end{array}$

And,

$\begin{array}{l}{s}_y=\sqrt{\frac{{\displaystyle \sum {\left(y-\overline{y}\right)}^2}}{n}}\\ s_y=\sqrt{\frac{483.77407}{27}}\\ s_y=\sqrt{17.91756}\end{array}$

Consider,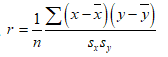

Putting the values in the formula,

$\begin{array}{l}r=\frac{1}{n}\frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{s_x{s}_y}\\ r=\frac{1}{27}\cdot \frac{283.16963}{\left(\sqrt{15.00488}\right)\left(\sqrt{17.91756}\right)}\\ r=0.63963\end{array}$

Putting the values to obtain $b_1$,

$\begin{array}{l}{b}_1=r\frac{s_y}{s_x}\\ b_1=\frac{1}{27}\cdot \frac{283.16963}{\left(\sqrt{15.00488}\right)\left(\sqrt{17.91756}\right)}\frac{\left(\sqrt{17.91756}\right)}{\left(\sqrt{15.00488}\right)}\\ b_1=0.699\end{array}$

Putting the values to obtain $b_0$,

$\begin{array}{l}{b}_0=\overline{y}-b_1\overline{x}\\ b_0=\left(182.31481\right)-\left(0.699\right)\left(227.02593\right)\\ b_0=23.6335\end{array}$

Hence, the least-square regression line is given by:

$\begin{array}{l}y=b_0+b_{1}x\\ y=\left(23.6335\right)+\left(0.699\right)x\\ y=0.699x+23.6335\end{array}$

Therefore, the least squares regression line for the given data set by removing the outlier is $y=0.699x+23.6335$

Hence the result is noticeably different.

To determine

The coefficient of determination for the data set with the outlier removed.

Answer to Problem 26E

$0.40912$.

Explanation of Solution

Given information:

Same as part $a$.

The months with two lowest exports are January and February $2011$.

Calculation:

From part $c$ of this exercise, the correlation coefficient with the outlier removed is $r=0.63963$

The coefficient of determination is given by:

$r^2$

Where $r$ is the correlation coefficient of the data.

Plugging the values to obtain Coefficient of Determination,

$r^2={\left(0.63963\right)}^2=0.409123\approx 0.40912$

Therefore, the Coefficient of Determination is $0.40912$.

To determine

To calculate:

To check for which data set will the proportion of variance explained by the least-squares regression line be greater.

Answer to Problem 26E

The proportion of variance explained by the least-squares regression line is greater for the data from January $2011$ through May $2013$.

Explanation of Solution

Given information:

Same as part $a$.

Two economists decide to study the relationship between imports and exports. One uses data from January $2011$ through May $2013$ and the other used data from March $2011$ through May $2013$.

Calculation:

From previous parts of this exercise,

The Coefficient of Determination is $0.64246$.

The Coefficient of Determination without the outliers is $0.40912$.

Here the coefficient of determination decreased without the outliers.

Hence, the proportion of variance explained is less without the outlier.

Therefore, the proportion of variance explained by the least-squares regression line is greater for the data from January $2011$ through May $2013$.