
Concept explainers
In a process that manufactures bearings, 90% of the bearings meet a thickness specification. A shipment contains 500 bearings. A shipment is acceptable if at least 440 of the 500 bearings meet the specification. Assume that each shipment contains a random sample of bearings.
a. What is the
b. What is the probability that more than 285 out of 300 shipments are acceptable?
c. What proportion of bearings must meet the specification in order that 99% of the shipments are acceptable?
a.
Find the probability that a given shipment is acceptable.
Answer to Problem 11E
The probability that a given shipment is acceptableis 0.9418.
Explanation of Solution
Given info:
About 90% of the bearings meet a thickness specification. In total there are 500 bearings. If at least 440 of 500 bearings meet specification then the shipment is acceptable.
Calculation:
The non-defective bearings in a shipment is denoted as X. Then X follows Binomial with parameters
The normal distribution can be used to approximate the binomial distribution with,
Mean:
Substitute 500 for n and 0.9 for p in the above equation.
Standard deviation:
Substitute 500 for n and 0.9 for p in the above equation.
The approximate binomial probability using the normal distribution is,
By using continuity correction, the value 0.5 is subtracted from the value of 440.
Substitute 440 for a,
The formula to convert X values into z score is,
Substitute 450for np and6.7082for
The above probability can be obtained by finding the areas to the left of –1.57.
The shaded region represents the area to the right of –1.57 is shown below:
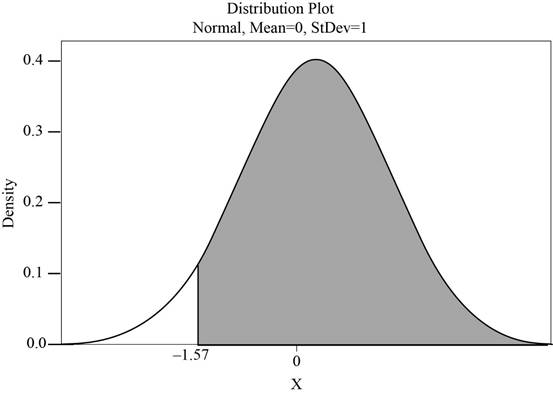
Use Table A.2: Cumulative Normal Distribution to find the area.
Procedure:
For z at –1.57,
- Locate –1.5 in the left column of the Table A.2.
- Obtain the value in the corresponding row below 0.07.
That is,
Then,
Thus, the probability that a given shipment is acceptable is 0.9418.
b.
Find probability that more than 285 out of 300 shipments are acceptable.
Answer to Problem 11E
The probability that more than 285 out of 300 shipments are acceptable is 0.2327.
Explanation of Solution
Calculation:
The random variable Y is defined as the number of shipments out of 300 that are acceptable.
From part (a), the probability that a given shipment is acceptable is 0.9418.
Then, the random variable Y follows binomial with
The normal distribution can be used to approximate the binomial distribution with,
Mean:
Substitute 300 for n and 0.9418 for p in the above equation.
Standard deviation:
Substitute n as 300 and 0.9418 for p in the above equation.
The approximate binomial probability using the normal distribution is,
By using continuity correction, the value 0.5 is added from the value of 285.
Substitute 285 for a,
The formula to convert X values into z score is,
Substitute 282.54for np and4.0551for
The above probability can be obtained by finding the areas to the left of 0.73.
The shaded region represents the area to the right of 0.73 is shown below:
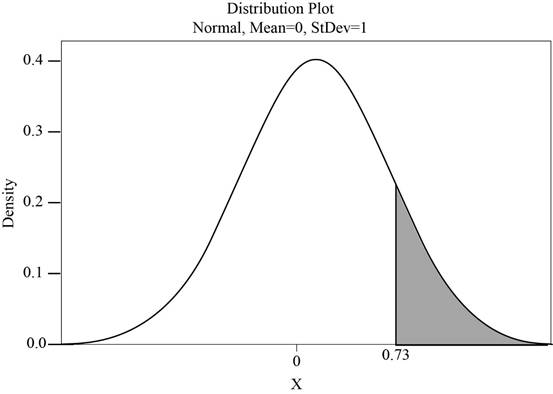
Use Table A.2: Cumulative Normal Distribution to find the area.
Procedure:
For z at 0.73,
- Locate0.7 in the left column of the Table A.2.
- Obtain the value in the corresponding row below 0.03.
That is,
Then,
Thus, the probability that more than 285 out of 300 shipments are acceptable is 0.2327.
c.
Find proportion of bearings must meet the specification in order that 99% of the shipments are acceptable.
Answer to Problem 11E
The proportion of bearings must meet the specification in order that 99% of the shipments are acceptable is 0.909.
Explanation of Solution
Calculation:
The required proportion of defective bearings is denoted as p and the number of defective bearings is denoted as X.
Then, the random variable X follows binomial with parameters
The normal distribution can be used to approximate the binomial distribution with,
Mean:
Substitute 500 for n in the above equation.
Standard deviation:
Substitute n as 500 in the above equation.
The probability that a shipment is acceptable is
The approximate binomial probability using the normal distribution is,
By using continuity correction, the value 0.5 is added from the value of 285.
Substitute 440 for a,
The formula to convert X values into z score is,
Substitute 500p for np and
The value of the random variable X for the top 0.99 is same as the value of X for the top 0.01. The area to the left of X is 0.01 and right of X is 0.99.
The shaded region represents of the area of 99% of the shipments that are acceptable is shown below:
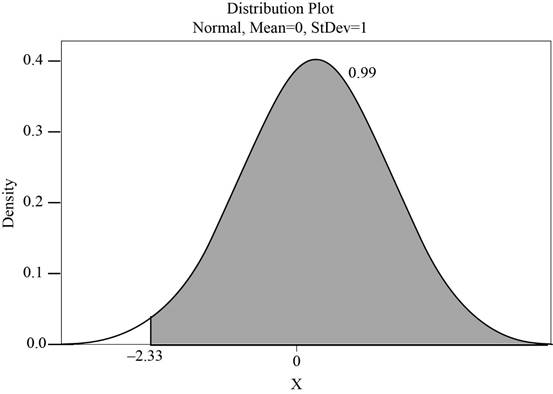
Use Table A.2: Cumulative Normal Distribution to find the critical value.
Procedure:
- Locate an approximate area of 0.0100 in the body of the A.2 table. The area closest to 0.0100 is 0.0099.
- Move left until the first column and note the value as –2.3.
- Move upward until the top row reached and note the value as 0.03.
Thus, the corresponding z-score is –2.33.
The z-score can be expressed in terms of p as follows:
Taking square on both sides,
Implies,
That is,
The formula for solving the quadratic equation of the form
Substitute
On solving this quadratic equation the value of p is,
Since 0.841 is a spurious root.
Thus, the proportion of bearings must meet the specification in order that 99% of the shipments are acceptable is 0.909.
Want to see more full solutions like this?
Chapter 4 Solutions
Statistics for Engineers and Scientists
- Microsoft Excel include formulasarrow_forwardQuestion 1 The data shown in Table 1 are and R values for 24 samples of size n = 5 taken from a process producing bearings. The measurements are made on the inside diameter of the bearing, with only the last three decimals recorded (i.e., 34.5 should be 0.50345). Table 1: Bearing Diameter Data Sample Number I R Sample Number I R 1 34.5 3 13 35.4 8 2 34.2 4 14 34.0 6 3 31.6 4 15 37.1 5 4 31.5 4 16 34.9 7 5 35.0 5 17 33.5 4 6 34.1 6 18 31.7 3 7 32.6 4 19 34.0 8 8 33.8 3 20 35.1 9 34.8 7 21 33.7 2 10 33.6 8 22 32.8 1 11 31.9 3 23 33.5 3 12 38.6 9 24 34.2 2 (a) Set up and R charts on this process. Does the process seem to be in statistical control? If necessary, revise the trial control limits. [15 pts] (b) If specifications on this diameter are 0.5030±0.0010, find the percentage of nonconforming bearings pro- duced by this process. Assume that diameter is normally distributed. [10 pts] 1arrow_forward4. (5 pts) Conduct a chi-square contingency test (test of independence) to assess whether there is an association between the behavior of the elderly person (did not stop to talk, did stop to talk) and their likelihood of falling. Below, please state your null and alternative hypotheses, calculate your expected values and write them in the table, compute the test statistic, test the null by comparing your test statistic to the critical value in Table A (p. 713-714) of your textbook and/or estimating the P-value, and provide your conclusions in written form. Make sure to show your work. Did not stop walking to talk Stopped walking to talk Suffered a fall 12 11 Totals 23 Did not suffer a fall | 2 Totals 35 37 14 46 60 Tarrow_forward
- Question 2 Parts manufactured by an injection molding process are subjected to a compressive strength test. Twenty samples of five parts each are collected, and the compressive strengths (in psi) are shown in Table 2. Table 2: Strength Data for Question 2 Sample Number x1 x2 23 x4 x5 R 1 83.0 2 88.6 78.3 78.8 3 85.7 75.8 84.3 81.2 78.7 75.7 77.0 71.0 84.2 81.0 79.1 7.3 80.2 17.6 75.2 80.4 10.4 4 80.8 74.4 82.5 74.1 75.7 77.5 8.4 5 83.4 78.4 82.6 78.2 78.9 80.3 5.2 File Preview 6 75.3 79.9 87.3 89.7 81.8 82.8 14.5 7 74.5 78.0 80.8 73.4 79.7 77.3 7.4 8 79.2 84.4 81.5 86.0 74.5 81.1 11.4 9 80.5 86.2 76.2 64.1 80.2 81.4 9.9 10 75.7 75.2 71.1 82.1 74.3 75.7 10.9 11 80.0 81.5 78.4 73.8 78.1 78.4 7.7 12 80.6 81.8 79.3 73.8 81.7 79.4 8.0 13 82.7 81.3 79.1 82.0 79.5 80.9 3.6 14 79.2 74.9 78.6 77.7 75.3 77.1 4.3 15 85.5 82.1 82.8 73.4 71.7 79.1 13.8 16 78.8 79.6 80.2 79.1 80.8 79.7 2.0 17 82.1 78.2 18 84.5 76.9 75.5 83.5 81.2 19 79.0 77.8 20 84.5 73.1 78.2 82.1 79.2 81.1 7.6 81.2 84.4 81.6 80.8…arrow_forwardName: Lab Time: Quiz 7 & 8 (Take Home) - due Wednesday, Feb. 26 Contingency Analysis (Ch. 9) In lab 5, part 3, you will create a mosaic plot and conducted a chi-square contingency test to evaluate whether elderly patients who did not stop walking to talk (vs. those who did stop) were more likely to suffer a fall in the next six months. I have tabulated the data below. Answer the questions below. Please show your calculations on this or a separate sheet. Did not stop walking to talk Stopped walking to talk Totals Suffered a fall Did not suffer a fall Totals 12 11 23 2 35 37 14 14 46 60 Quiz 7: 1. (2 pts) Compute the odds of falling for each group. Compute the odds ratio for those who did not stop walking vs. those who did stop walking. Interpret your result verbally.arrow_forwardSolve please and thank you!arrow_forward
- 7. In a 2011 article, M. Radelet and G. Pierce reported a logistic prediction equation for the death penalty verdicts in North Carolina. Let Y denote whether a subject convicted of murder received the death penalty (1=yes), for the defendant's race h (h1, black; h = 2, white), victim's race i (i = 1, black; i = 2, white), and number of additional factors j (j = 0, 1, 2). For the model logit[P(Y = 1)] = a + ß₁₂ + By + B²², they reported = -5.26, D â BD = 0, BD = 0.17, BY = 0, BY = 0.91, B = 0, B = 2.02, B = 3.98. (a) Estimate the probability of receiving the death penalty for the group most likely to receive it. [4 pts] (b) If, instead, parameters used constraints 3D = BY = 35 = 0, report the esti- mates. [3 pts] h (c) If, instead, parameters used constraints Σ₁ = Σ₁ BY = Σ; B = 0, report the estimates. [3 pts] Hint the probabilities, odds and odds ratios do not change with constraints.arrow_forwardSolve please and thank you!arrow_forwardSolve please and thank you!arrow_forward
- Question 1:We want to evaluate the impact on the monetary economy for a company of two types of strategy (competitive strategy, cooperative strategy) adopted by buyers.Competitive strategy: strategy characterized by firm behavior aimed at obtaining concessions from the buyer.Cooperative strategy: a strategy based on a problem-solving negotiating attitude, with a high level of trust and cooperation.A random sample of 17 buyers took part in a negotiation experiment in which 9 buyers adopted the competitive strategy, and the other 8 the cooperative strategy. The savings obtained for each group of buyers are presented in the pdf that i sent: For this problem, we assume that the samples are random and come from two normal populations of unknown but equal variances.According to the theory, the average saving of buyers adopting a competitive strategy will be lower than that of buyers adopting a cooperative strategy.a) Specify the population identifications and the hypotheses H0 and H1…arrow_forwardYou assume that the annual incomes for certain workers are normal with a mean of $28,500 and a standard deviation of $2,400. What’s the chance that a randomly selected employee makes more than $30,000?What’s the chance that 36 randomly selected employees make more than $30,000, on average?arrow_forwardWhat’s the chance that a fair coin comes up heads more than 60 times when you toss it 100 times?arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill



