
Lenovo uses the ZX-81 chip in some of its laptop computers. The prices for the chip during the past 12 months were as follows:

a) Use a 2-month moving average on all the data and plot the averages and the prices.
b) Use a 3-month moving average and add the 3-month plot to the graph created in part (a).
c) Which is better (using the mean absolute deviation): the 2-month average or the 3-month average?
d) Compute the
a)
To determine:Plot and graphically represent the averages and the prices using 2-month moving average.
Introduction: Forecasting is used to predict future changes or a demand pattern. It involves different approaches and varies with different time periods. Moving average, weighted moving average and exponential smoothing are the time series methods of forecasting which uses past data to forecast the future.
Answer to Problem 9P
By using 2-month moving average, the averages and the prices are plotted.
Explanation of Solution
Given information:
| Month | Price Per Chip |
| January | 1.80 |
| February | 1.67 |
| March | 1.70 |
| April | 1.85 |
| May | 1.90 |
| June | 1.87 |
| July | 1.80 |
| August | 1.83 |
| September | 1.70 |
| October | 1.65 |
| November | 1.70 |
| December | 1.75 |
Formula to calculate the forecasted demand
| Month | Price Per Chip $ | Moving Average |
| January | 1.8 | |
| February | 1.67 | |
| March | 1.7 | 1.735 |
| April | 1.85 | 1.685 |
| May | 1.9 | 1.775 |
| June | 1.87 | 1.875 |
| July | 1.8 | 1.885 |
| August | 1.83 | 1.835 |
| September | 1.7 | 1.815 |
| October | 1.65 | 1.765 |
| November | 1.7 | 1.675 |
| December | 1.75 | 1.675 |
Table 1
Excel worksheet:
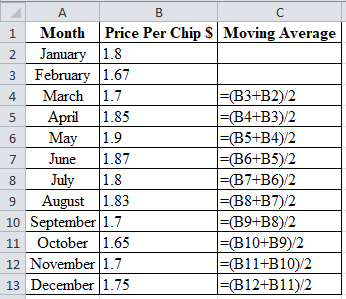
Calculation of the forecast for March:
To calculate the forecast for March, divide the summation of the values of January and February by 2. The corresponding value 1.735 is the forecast for March. The 2-month moving average for the month of March is 1.735.
Calculation of the forecast for April:
To calculate the forecast for April, divide the summation of the values of February and March by 2. The corresponding value 1.685 is the forecast for April. The 2-month moving average for the month of April is 1.685.
Calculation of the forecast for May:
To calculate the forecast for May, divide the summation of the values of March and April by 2. The corresponding value 1.775 is the forecast for May. The 2-month moving average for the month of May is 1.775.
Calculation of the forecast for June:
To calculate the forecast for June, divide the summation of the values of April and May by 2. The corresponding value 1.875 is the forecast for June. The 2-month moving average for the month of June is 1.875.
Calculation of the forecast for July:
To calculate the forecast for July, divide the summation of the values of May and June by 2. The corresponding value 1.885 is the forecast for July. The 2-month moving average for the month of July is 1.885
Calculation of the forecast for August:
To calculate the forecast for August, divide the summation of the values of June and July by 2. The corresponding value 1.835 is the forecast for August. The 2-month moving average for the month of August is 1.685.
Calculation of the forecast for September:
To calculate the forecast for September, divide the summation of the values of July and August by 2. The corresponding value 1.815 is the forecast for September. The 2-month moving average for the month of September is 1.815.
Calculation of the forecast for October:
To calculate the forecast for October, divide the summation of the values of August and September by 2. The corresponding value 1.765 is the forecast for October. The 2-month moving average for the month of October is 1.765.
Calculation of the forecast for November:
To calculate the forecast for November, divide the summation of the values of September and October by 2. The corresponding value 1.675 is the forecast for November. The 2-month moving average for the month of November is 1.675.
Calculation of the forecast for December:
To calculate the forecast for December, divide the summation of the values of October and November by 2. The corresponding value 1.675 is the forecast for December. The 2-month moving average for the month of December is 1.675.
Graph:
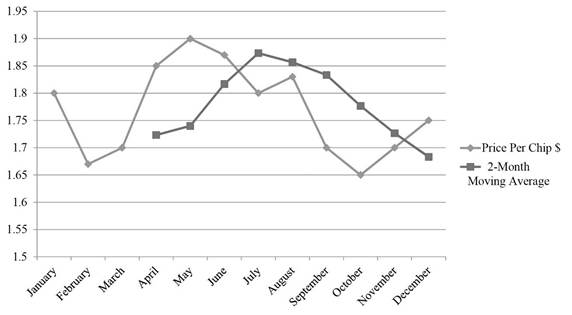
The data for 2-month moving average is obtained from Table 1. Graph is plotted with price per chip, and 2-month moving average.
Hence, the graphical representation of the averages and the prices are plotted using 2-month moving average.
b)
To determine:Plot and graphically represent the averages and the prices using 3-month moving average.
Answer to Problem 9P
By using 3-month moving average, the averages and the prices are plotted.
Explanation of Solution
Given information:
| Month | Price Per Chip |
| January | 1.80 |
| February | 1.67 |
| March | 1.70 |
| April | 1.85 |
| May | 1.90 |
| June | 1.87 |
| July | 1.80 |
| August | 1.83 |
| September | 1.70 |
| October | 1.65 |
| November | 1.70 |
| December | 1.75 |
Formula to calculate the forecasted demand:
| Month | Price Per Chip $ | Moving Average |
| January | 1.8 | |
| February | 1.67 | |
| March | 1.7 | |
| April | 1.85 | 1.723 |
| May | 1.9 | 1.740 |
| June | 1.87 | 1.817 |
| July | 1.8 | 1.873 |
| August | 1.83 | 1.857 |
| September | 1.7 | 1.833 |
| October | 1.65 | 1.777 |
| November | 1.7 | 1.727 |
| December | 1.75 | 1.683 |
Table 2
Excel worksheet:
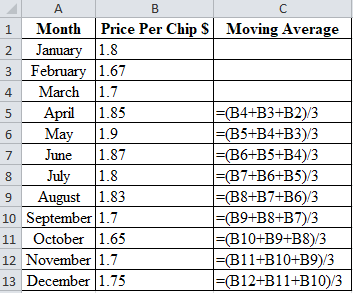
Calculation of the forecast for April:
To calculate the forecast for April, divide the summation of the values of January, February and March by 3. The corresponding value 1.732 is the forecast for April. Therefore, 3-month moving average for the month of April is 1.723.
Calculation of the forecast for May:
To calculate the forecast for May, divide the summation of the values of February, March and April by 3. The corresponding value 1.740 is the forecast for May. Therefore, 3-month moving average for the month of May is 1.740.
Calculation of the forecast for June:
To calculate the forecast for June, divide the summation of the values of March, April and May by 3. The corresponding value 1.817 is the forecast for June. Therefore, 3-month moving average for the month of June is 1.817.
Calculation of the forecast for July:
To calculate the forecast for July, divide the summation of the values of April, May and June by 3. The corresponding value 1.873 is the forecast for July. Therefore, 3-month moving average for the month of July is 1.873.
Calculation of the forecast for August:
To calculate the forecast for August, divide the summation of the values of May, June and July by 3. The corresponding value 1.873 is the forecast for August. Therefore, 3-month moving average for the month of August is 1.873.
Calculation of the forecast for September:
To calculate the forecast for September, divide the summation of the values of June, July and August by 3. The corresponding value 1.833 is the forecast for September. Therefore, 3-month moving average for the month of June is 1.833.
Calculation of the forecast for October:
To calculate the forecast for October, divide the summation of the values of July, August and September by 3. The corresponding value 1.777 is the forecast for October. Therefore, 3-month moving average for the month of June is 1.777.
Calculation of the forecast for November:
To calculate the forecast for November, divide the summation of the values of August, September and October by 3. The corresponding value 1.727 is the forecast for November. Therefore, 3-month moving average for the month of November is 1.727.
Calculation of the forecast for December:
To calculate the forecast for December, divide the summation of the values of September, October and November by 3. The corresponding value 1.683 is the forecast for December. Therefore, 3-month moving average for the month of December is 1.683.
Graph:
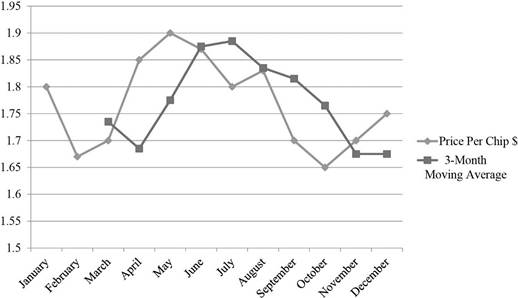
The data for 3-month moving average is obtained from Table 2. Graph is plotted with price per chip, and 3-month moving average.
Hence, the graphical representation of the averages and the prices are plotted using 3-month moving average.
c)
To determine:Compute the Mean Absolute Deviation (MAD) using 2-month moving average and 3-month moving average and from the results, infer the superior method.
Answer to Problem 9P
MAD from 2-month moving average and 3-month moving average are 0.075 & 0.079 (refer to equations (1) & (2)). Because of less deviation of error, MAD from a 2-month moving average is superior over a 3-month moving average.
Explanation of Solution
Given information:
| Month | Price Per Chip |
| January | 1.80 |
| February | 1.67 |
| March | 1.70 |
| April | 1.85 |
| May | 1.90 |
| June | 1.87 |
| July | 1.80 |
| August | 1.83 |
| September | 1.70 |
| October | 1.65 |
| November | 1.70 |
| December | 1.75 |
Formula to calculate MAD:
Calculation of MAD using 2-month moving average:
Table 1 provides the calculation of forecast using 2-month moving average.
| Month | Price Per Chip $ | 2-month moving average | Absolute error |
| January | 1.8 | ||
| February | 1.67 | ||
| March | 1.7 | 1.735 | 0.035 |
| April | 1.85 | 1.685 | 0.165 |
| May | 1.9 | 1.775 | 0.125 |
| June | 1.87 | 1.875 | 0.005 |
| July | 1.8 | 1.885 | 0.085 |
| August | 1.83 | 1.835 | 0.005 |
| September | 1.7 | 1.815 | 0.115 |
| October | 1.65 | 1.765 | 0.115 |
| November | 1.7 | 1.675 | 0.025 |
| December | 1.75 | 1.675 | 0.075 |
| Total | 0.75 | ||
| MAD | 0.075 |
Excel worksheet:
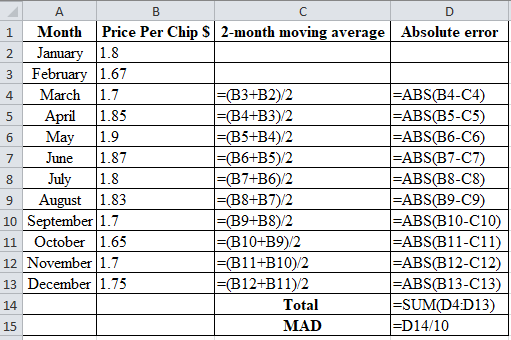
Calculation of the absolute error for March:
Absolute Error of March is the modulus of the difference between 1.7 and 1.735, which corresponds to 0.035. Therefore Absolute Error for March is 0.035.
Calculation of the absolute error for April:
Absolute Error of April is the modulus of the difference between 1.85 and 1.685, which corresponds to 0.165. Therefore Absolute Error for April is 0.165.
Calculation of the absolute error for May:
Absolute Error of May is the modulus of the difference between 1.9 and 1.775, which corresponds to 0.125. Therefore Absolute Error for May is 0.125.
Calculation of the absolute error for June:
Absolute Error of June is the modulus of the difference between 1.87 and 1.875, which corresponds to 0.005. Therefore Absolute Error for June is 0.005.
Calculation of the absolute error for July:
Absolute Error of July is the modulus of the difference between 1.8 and 1.885, which corresponds to 0.085. Therefore Absolute Error for July is 0.085.
Calculation of the absolute error for August:
Absolute Error of August is the modulus of the difference between 1.83 and 1.835, which corresponds to 0.005. Therefore Absolute Error for August is 0.005.
Calculation of the absolute error for September:
Absolute Error of September is the modulus of the difference between 1.7 and 1.815, which corresponds to 0.115. Therefore Absolute Error for September is 0.115.
Calculation of the absolute error for October:
Absolute Error of October is the modulus of the difference between 1.65 and 1.765, which corresponds to 0.115. Therefore Absolute Error for October is 0.115.
Calculation of the absolute error for November:
Absolute Error of November is the modulus of the difference between 1.7 and 1.675, which corresponds to 0.025. Therefore Absolute Error for November is 0.025.
Calculation of the absolute error for December:
Absolute Error of December is the modulus of the difference between 1.75 and 1.675, which corresponds to 0.075. Therefore Absolute Error for December is 0.075.
Calculation of MAD using 2-month moving average:
Mean Absolute Deviation is obtained by dividing the summation of absolute values by the number of years. Absolute error is obtained by taking modulus for the difference between Actual and forecasted values.
Substitute the summation value of absolute error for 10 years i.e. 0.75 is divided by number of years i.e. 10 yields MAD of 0.075
The Mean Absolute Deviation using 2-month moving average is 0.075
Calculation of MAD using 3-month moving average
Table 2 provides the value of 3-month moving average
| Month | Price Per Chip $ | 3-month Moving Average | Absolute error |
| January | 1.8 | ||
| February | 1.67 | ||
| March | 1.7 | ||
| April | 1.85 | 1.723 | 0.127 |
| May | 1.9 | 1.740 | 0.160 |
| June | 1.87 | 1.817 | 0.053 |
| July | 1.8 | 1.873 | 0.073 |
| August | 1.83 | 1.857 | 0.027 |
| September | 1.7 | 1.833 | 0.133 |
| October | 1.65 | 1.777 | 0.127 |
| November | 1.7 | 1.727 | 0.027 |
| December | 1.75 | 1.683 | 0.067 |
| Total | 0.793 | ||
| MAD | 0.079 |
Excel worksheet:
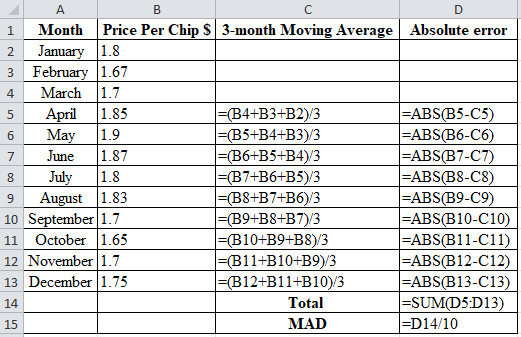
Calculation of the Absolute Error for April:
Absolute Error of April is the modulus of the difference between 1.85 and 1.723, which corresponds to 0.127. Absolute Error for April is 0.127
Calculation of the Absolute Error for May:
Absolute Error of May is the modulus of the difference between 1.9 and 1.740, which corresponds to 0.160. Therefore Absolute Error for May is 0.160
Calculation of the Absolute Error for June:
Absolute Error of June is the modulus of the difference between 1.87 and 1.817, which corresponds to 0.053. Therefore Absolute Error for June is 0.053
Calculation of the Absolute Error for July:
Absolute Error of July is the modulus of the difference between 1.8 and 1.873, which corresponds to 0.073. Absolute Error for July is 0.073.
Calculation of the Absolute Error for August:
Absolute Error of August is the modulus of the difference between 1.83 and 1.857, which corresponds to 0.027. Therefore, Absolute Error for August is 0.027.
Calculation of the Absolute Error for September:
Absolute Error of September is the modulus of the difference between 1.7 and 1.833, which corresponds to 0.133. Therefore Absolute Error for September is 0.133.
Calculation of the Absolute Error for October:
Absolute Error of October is the modulus of the difference between 1.65 and 1.777, which corresponds to 0.127. Therefore Absolute Error for October is 0.127.
Calculation of the Absolute Error for November:
Absolute Error of November is the modulus of the difference between 1.7 and 1.727, which corresponds to 0.027. Therefore Absolute Error for November is 0.027
Calculation of the Absolute Error for December:
Absolute Error of December is the modulus of the difference between 1.75 and 1.683, which corresponds to 0.067. Therefore Absolute Error for December is 0.067
Calculation of MAD using 3-month moving average:
Substitute the summation value of absolute error for 10 years i.e. 0.793 is divided by number of years i.e. 9 yields MAD of 0.079. Mean Absolute Deviation using 3-month moving average is 0.079
Hence, the Mean Absolute Deviation from the 2-month moving average is 0.075 (refer to equation (1)) and from the 3-month moving average is 0.079 (refer to equation (2)). Due to less deviation of error, the MAD from the 2-month moving average is superior to that of the 3-month moving average.
d)
To determine: Decide the best method by computing Mean Absolute Duration using exponential smoothing with α = 0.1, α = 0.3 and α = 0.5
Answer to Problem 9P
The Mean Absolute Deviation using exponential smoothing using α = 0.1 is 0.071, (refer to equation 3), α = 0.3 is 0.070 (refer to equation 4) and α = 0.5 is 0.066 (refer to equation 5). MAD using α = 0.5 is the best method since the MAD is minimum.
Explanation of Solution
Given information:
| Month | Price Per Chip |
| January | 1.80 |
| February | 1.67 |
| March | 1.70 |
| April | 1.85 |
| May | 1.90 |
| June | 1.87 |
| July | 1.80 |
| August | 1.83 |
| September | 1.70 |
| October | 1.65 |
| November | 1.70 |
| December | 1.75 |
The initial forecast for the month of January is $1.80
Formula to calculate the forecasted demand
Where,
Calculation of MAD using exponential smoothing with smoothing constant α = 0.1
| Sl. No. | Month | Price Per Chip $ | Forecast | Absolute error |
| 1 | January | 1.8 | 1.8 | 0 |
| 2 | February | 1.67 | 1.8 | 0.130 |
| 3 | March | 1.7 | 1.787 | 0.087 |
| 4 | April | 1.85 | 1.778 | 0.072 |
| 5 | May | 1.9 | 1.785 | 0.115 |
| 6 | June | 1.87 | 1.797 | 0.073 |
| 7 | July | 1.8 | 1.804 | 0.004 |
| 8 | August | 1.83 | 1.804 | 0.026 |
| 9 | September | 1.7 | 1.806 | 0.106 |
| 10 | October | 1.65 | 1.796 | 0.146 |
| 11 | November | 1.7 | 1.781 | 0.081 |
| 12 | December | 1.75 | 1.773 | 0.023 |
| Total | 0.8632 | |||
| MAD | 0.0719 |
Excel worksheet:
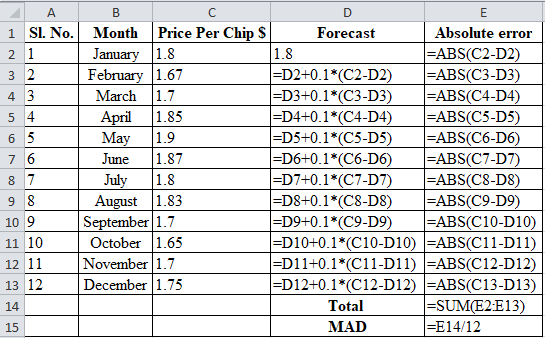
Calculation of absolute error for January:
Absolute Error of January is the modulus of the difference between 1.8 and 1.8, which corresponds to 0. Therefore Absolute Error for January is 0
Calculation of the forecast & absolute error for February:
To calculate forecast for February, substitute the value of forecast of January, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for February is 1.8
Absolute Error of February is the modulus of the difference between 1.67 and 1.8, which corresponds to 0.130 Therefore Absolute Error for February, is 0.130
Forecast and Absolute error for February is 1.8 & 0.130
Calculation of the forecast & absolute error for March:
To calculate forecast for March, substitute the value of forecast of February, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for March is 1.787
Absolute Error of March is the modulus of the difference between 1.7 and 1.787, which corresponds to 0.087 Therefore Absolute Error for March, is 0.087
Forecast and Absolute error for March is 1.787 & 0.087
Calculation of the forecast & absolute error for April:
To calculate forecast for April, substitute the value of forecast of March, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for April is 1.778.
Absolute Error of April is the modulus of the difference between 1.85 and 1.778, which corresponds to 0.072. Therefore Absolute Error for April is 0.087.
Forecast and Absolute error for April is 1.778 & 0.072.
Calculation of the forecast & absolute error for May:
To calculate forecast for May, substitute the value of forecast of April, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for May is 1.785
Absolute Error of May is the modulus of the difference between 1.9 and 1.785, which corresponds to 0.115. Therefore Absolute Error for May is 0.115
Forecast and Absolute error for May is 1.785 & 0.115
Calculation of the forecast & absolute error for June:
To calculate forecast for June, substitute the value of forecast of May, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for June is 1.797.
Absolute Error of June is the modulus of the difference between 1.87 and 1.797, which corresponds to 0.073. Therefore Absolute Error for June is 0.073.
Forecast and Absolute error for June is 1.797 & 0.073.
Calculation of the forecast & absolute error for July:
To calculate forecast for July, substitute the value of forecast of June, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for July is 1.804
Absolute Error of July is the modulus of the difference between 1.8 and 1.804, which corresponds to 0.004. Therefore Absolute Error for July is 0.004
Forecast and Absolute error for July is 1.804 & 0.004
Calculation of the forecast & absolute error for August:
To calculate forecast for August, substitute the value of forecast of July, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for August is 1.804
Absolute Error of August is the modulus of the difference between 1.83 and 1.804, which corresponds to 0.026. Therefore Absolute Error for July is 0.026
Forecast and Absolute error for August is 1.804 & 0.026
Calculation of the forecast & absolute error for September:
To calculate forecast for September, substitute the value of forecast of August, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for September is 1.806
Absolute Error of September is the modulus of the difference between 1.7 and 1.806, which corresponds to 0.106 Therefore Absolute Error for September, is 0.106
Forecast and Absolute error for September is 1.806 & 0.106
Calculation of the forecast & absolute error for October:
To calculate forecast for October, substitute the value of forecast of September, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for October is 1.796
Absolute Error of October is the modulus of the difference between 1.65 and 1.796, which corresponds to 0.146 Therefore Absolute Error for October, is 0.146
Forecast and Absolute error for October is 1.796 & 0.146
Calculation of the forecast & absolute error for November:
To calculate forecast for November, substitute the value of forecast of October, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for November is 1.781.
Absolute Error of November is the modulus of the difference between 1.7 and 1.781, which corresponds to 0.081 Therefore Absolute Error for November, is 0.081.
Forecast and Absolute error for November is 1.781 & 0.081.
Calculation of the forecast & absolute error for December:
To calculate forecast for December, substitute the value of forecast of November, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for December is 1.773.
Absolute Error of December is the modulus of the difference between 1.75 and 1.773, which corresponds to 0.023. Therefore Absolute Error for December is 0.023.
Forecast and Absolute error for December is 1.773 & 0.023.
Calculation of MAD:
Upon substitution of summation value of absolute error for 12 years i.e. 0.8623 is divided by number of years i.e. 12 yields MAD of 0.0719
Mean Absolute Deviation using exponential smoothing with smoothing constant α = 0.1 is 0.0719
Calculation of MAD using exponential smoothing with smoothing constant α = 0.3
| Sl. No. | Month | Price Per Chip $ | Forecast | Absolute error |
| 1 | January | 1.8 | 1.8 | 0 |
| 2 | February | 1.67 | 1.800 | 0.130 |
| 3 | March | 1.7 | 1.761 | 0.061 |
| 4 | April | 1.85 | 1.743 | 0.107 |
| 5 | May | 1.9 | 1.775 | 0.125 |
| 6 | June | 1.87 | 1.812 | 0.058 |
| 7 | July | 1.8 | 1.830 | 0.030 |
| 8 | August | 1.83 | 1.821 | 0.009 |
| 9 | September | 1.7 | 1.824 | 0.124 |
| 10 | October | 1.65 | 1.786 | 0.136 |
| 11 | November | 1.7 | 1.746 | 0.046 |
| 12 | December | 1.75 | 1.732 | 0.018 |
| Total | 0.844 | |||
| MAD | 0.070 |
Excel worksheet:

Calculation of the absolute error for January:
Absolute Error of January is the modulus of the difference between 1.8 and 1.8, which corresponds to 0. Therefore Absolute Error for January is 0
Calculation of the forecast & absolute error for February:
To calculate forecast for February, substitute the value of forecast of January, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for February is 1.8.
Absolute Error of February is the modulus of the difference between 1.67 and 1.8, which corresponds to 0.130 Therefore Absolute Error for February, is 0.130.
Forecast and Absolute error for February is 1.800 & 0.130.
Calculation of the forecast & absolute error for March:
To calculate forecast for March, substitute the value of forecast of February, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for March is 1.761.
Absolute Error of March is the modulus of the difference between 1.7 and 1.761, which corresponds to 0.061 Therefore Absolute Error for March, is 0.061.
Forecast and Absolute error for March is 1.761 & 0.061.
Calculation of the forecast & absolute error for April:
To calculate forecast for April, substitute the value of forecast of March, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for April is 1.743.
Absolute Error of April is the modulus of the difference between 1.85 and 1.743, which corresponds to 0.107. Therefore Absolute Error for April is 0.107.
Forecast and Absolute error for April is 1.743 & 0.107.
Calculation of the forecast & absolute error for May:
To calculate forecast for May, substitute the value of forecast of April, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for May is 1.775.
Absolute Error of May is the modulus of the difference between 1.9 and 1.775, which corresponds to 0.125. Therefore Absolute Error for May is 0.125.
Forecast and Absolute error for May is 1.775 & 0.125.
Calculation of the forecast & absolute error for June:
To calculate forecast for June, substitute the value of forecast of May, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for June is 1.812.
Absolute Error of June is the modulus of the difference between 1.87 and 1.812, which corresponds to 0.058. Therefore Absolute Error for June is 0.058.
Forecast and Absolute error for June is 1.812 & 0.058.
Calculation of the forecast & absolute error for July:
To calculate forecast for July, substitute the value of forecast of June, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for July is 1.830.
Absolute Error of July is the modulus of the difference between 1.8 and 1.830, which corresponds to 0.030. Therefore Absolute Error for July is 0.030.
Forecast and Absolute error for July is 1.830 & 0.030.
Calculation of the forecast & absolute error for August:
To calculate forecast for August, substitute the value of forecast of July, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for August is 1.821.
Absolute Error of August is the modulus of the difference between 1.83 and 1.821, which corresponds to 0.009. Therefore Absolute Error for July is 0.009.
Forecast and Absolute error for August is 1.821 & 0.009.
Calculation of the forecast & absolute error for September:
To calculate forecast for September, substitute the value of forecast of August, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for September is 1.824.
Absolute Error of September is the modulus of the difference between 1.7 and 1.824, which corresponds to 0.124 Therefore Absolute Error for September, is 0.124.
Forecast and Absolute error for September is 1.824 & 0.124.
Calculation of the forecast & absolute error for October:
To calculate forecast for October, substitute the value of forecast of September, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for October is 1.786.
Absolute Error of October is the modulus of the difference between 1.65 and 1.786, which corresponds to 0.146 Therefore Absolute Error for October, is 0.136.
Forecast and Absolute error for October is 1.786 & 0.136.
Calculation of the forecast & absolute error for November:
To calculate forecast for November, substitute the value of forecast of October, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for November is 1.746.
Absolute Error of November is the modulus of the difference between 1.7 and 1.746, which corresponds to 0.046 Therefore Absolute Error for November, is 0.046.
Forecast and Absolute error for November is 1.746 & 0.046.
Calculation of the forecast & absolute error for December:
To calculate forecast for December, substitute the value of forecast of November, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for December is 1.732.
Absolute Error of December is the modulus of the difference between 1.75 and 1.773, which corresponds to 0.018. Therefore Absolute Error for December is 0.018.
Forecast and Absolute error for December is 1.732 & 0.018.
Calculation of the Mean Absolute Deviation:
Upon substitution of summation value of absolute error for 12 years i.e. 0.844 is divided by number of years i.e. 12 yields MAD of 0.070.
Mean Absolute Deviation using exponential smoothing with smoothing constant α = 0.3 is 0.070
Calculation of MAD using exponential smoothing with smoothing constant α = 0.5
| Sl. No. | Month | Price Per Chip $ | Forecast | Absolute error |
| 1 | January | 1.8 | 1.8 | 0 |
| 2 | February | 1.67 | 1.800 | 0.130 |
| 3 | March | 1.7 | 1.735 | 0.035 |
| 4 | April | 1.85 | 1.718 | 0.133 |
| 5 | May | 1.9 | 1.784 | 0.116 |
| 6 | June | 1.87 | 1.842 | 0.028 |
| 7 | July | 1.8 | 1.856 | 0.056 |
| 8 | August | 1.83 | 1.828 | 0.002 |
| 9 | September | 1.7 | 1.829 | 0.129 |
| 10 | October | 1.65 | 1.764 | 0.114 |
| 11 | November | 1.7 | 1.707 | 0.007 |
| 12 | December | 1.75 | 1.704 | 0.046 |
| Total | 0.797 | |||
| MAD | 0.066 |
Excel worksheet:

Calculation of the absolute error for January:
Absolute Error of January is the modulus of the difference between 1.8 and 1.8, which corresponds to 0. Therefore Absolute Error for January is 0
Absolute Error for January is 0
Calculation of the forecast & absolute error for February:
To calculate forecast for February, substitute the value of forecast of January, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for February is 1.8
Absolute Error of February is the modulus of the difference between 1.67 and 1.8, which corresponds to 0.130 Therefore Absolute Error for February, is 0.130
Forecast and Absolute error for February is 1.8 & 0.130
Calculation of the forecast & absolute error for March:
To calculate forecast for March, substitute the value of forecast of February, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for March is 1.735
Absolute Error of March is the modulus of the difference between 1.7 and 1.735, which corresponds to 0.035 Therefore Absolute Error for March, is 0.035
Forecast and Absolute error for March is 1.735 & 0.035
Calculation of the forecast & absolute error for April:
To calculate forecast for April, substitute the value of forecast of March, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for April is 1.718
Absolute Error of April is the modulus of the difference between 1.85 and 1.718, which corresponds to 0.133. Therefore Absolute Error for April is 0.133
Forecast and Absolute error for April is 1.718 & 0.133
Calculation of the forecast & absolute error for May:
To calculate forecast for May, substitute the value of forecast of April, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for May is 1.784
Absolute Error of May is the modulus of the difference between 1.9 and 1.784, which corresponds to 0.116. Therefore Absolute Error for May is 0.116
Forecast and Absolute error for May is 1.784 & 0.116
Calculation of the forecast & absolute error for June:
To calculate forecast for June, substitute the value of forecast of May, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for June is 1.842.
Absolute Error of June is the modulus of the difference between 1.87 and 1.842, which corresponds to 0.028. Therefore Absolute Error for June is 0.028.
Forecast and Absolute error for June is 1.842 & 0.028.
Calculation of the forecast & absolute error for July:
To calculate forecast for July, substitute the value of forecast of June, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for July is 1.856.
Absolute Error of July is the modulus of the difference between 1.8 and 1.856, which corresponds to 0.056. Therefore Absolute Error for July is 0.056.
Forecast and Absolute error for July is 1.856 & 0.056.
Calculation of the forecast & absolute error for August:
To calculate forecast for August, substitute the value of forecast of July, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for August is 1.828.
Absolute Error of August is the modulus of the difference between 1.83 and 1.828, which corresponds to 0.002. Therefore Absolute Error for July is 0.002.
Forecast and Absolute error for August is 1.828 & 0.002.
Calculation of the forecast & absolute error for September:
To calculate forecast for September, substitute the value of forecast of August, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for September is 1.829.
Absolute Error of September is the modulus of the difference between 1.7 and 1.829, which corresponds to 0.129 Therefore Absolute Error for September, is 0.129.
Forecast and Absolute error for September is 1.829 & 0.129.
Calculation of the forecast & absolute error for October:
To calculate forecast for October, substitute the value of forecast of September, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for October is 1.764.
Absolute Error of October is the modulus of the difference between 1.65 and 1.764, which corresponds to 0.114 Therefore Absolute Error for October, is 0.114.
Forecast and Absolute error for October is 1.764 & 0.114.
Calculation of the forecast & absolute error for November:
To calculate forecast for November, substitute the value of forecast of October, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for November is 1.707.
Absolute Error of November is the modulus of the difference between 1.7 and 1.707, which corresponds to 0.007 Therefore Absolute Error for November, is 0.007.
Forecast and Absolute error for November is 1.707 & 0.007.
Calculation of the forecast & absolute error for December:
To calculate forecast for December, substitute the value of forecast of November, smoothing constant and difference of actual and forecasted demand in the above formula. The result of forecast for December is 1.704.
Absolute Error of December is the modulus of the difference between 1.75 and 1.704, which corresponds to 0.046. Therefore Absolute Error for December is 0.046.
Forecast and Absolute error for December is 1.704 & 0.046.
Calculation of the Mean Absolute Deviation:
Upon substitution of summation value of absolute error for 11 years i.e. 0.797 is divided by number of years i.e. 12 yields MAD of 0.066.
Mean Absolute Deviation using exponential smoothing with smoothing constant α = 0.1 is 0.066
Hence, the Mean Absolute Deviation using exponential smoothing using α = 0.1 is 0.071, (refer equation 3) α = 0.3 is 0.070 (refer equation 4) and α = 0.5 is 0.066 (refer equation 5). MAD using α = 0.5 is the best method since the MAD is minimum.
Want to see more full solutions like this?
Chapter 4 Solutions
PRIN.OF OPERATIONS MANAGEMENT-MYOMLAB
- Davison Electronics manufactures three LED television monitors, identified as Model A, Model B, and Model C. Davison Electronics four manufacturing plants. Each model has its lowest possible production cost when produced at Plant 1. However, Plant 1 does not have the capacity to handle the total production of all three models. As a result, at least some of the production must be routed to the other manufacturing plants. The following table shows the minimum production requirements for next month, the plant capacities in units per month, and the production cost per unit at each plant: Model Production Cost per Unit Minimum Production Requirements Plant 1 Plant 2 Plant 3 Plant 4 A $25 $28 $37 $34 48,000 B $26 $35 $36 $41 75,000 C $20 $31 $26 $23 60,000 Production Capacity 65,000 50,000 32,000 43,000 Davison’s objective is to determine the cost-minimizing production planarrow_forwardAnecdotally, entrepreneurs frequently encounter two critical dilemmas in managing human resources: the timing of hiring and the decision regarding hiring a generalist versus a specialist for their growing venture. Deciding when to expand a team is crucial, as premature hiring (i.e., hiring too soon) can strain resources, while delayed hiring (i.e., hiring too late) might hinder growth opportunities. Moreover, the choice between hiring a generalist or a specialist depends on the specific needs and stage of the venture, with each option presenting distinct advantages and challenges. To address these issues, a management scholar seeks to identify the factors shaping the hiring cycle throughout the entrepreneurial journey and to understand the criteria for choosing between generalists and specialists at various stages of a venture. The scholar has assembled a sample of 20 experienced South African entrepreneurs who have encountered both failure and success in the financial technology…arrow_forward3. [25 pts.] Four projects are available for investment. The projects require the cash flows and yield the net present values (NPV) (in millions) shown in the following table. Project id. 1 2 Cash outflow at time 0 (million Lira) 8 8 NPV (million Lira) 12 11 3 4 6 5 8 6 If 20 million Lira is available for investment at time 0, find the investment plan that maximizes NPV. All investments are required to be 0 or 1 (fractional investment values are not permitted). a. Formulate the mathematical model. (Write the decision variables, objective function and the constraints.) [10 pts.] b. Find the optimal solution by using Branch and Bound method (Draw the branch and bound tree clearly, write also lower bounds(LB)) (Left branches x=0, right branches x =1) [15 pts.].arrow_forward
- examine the production concept and operations management, what are the key steps required to achieve success? Be specific in your response.arrow_forwardProduce a 3000 report with references on one international organization of your choice and Address the following: Provide a brief introduction of the organisation and sector it operates in, including its mission and vision statements, its core values, a summary of its financial performance and a general overview of the business’s operational activities. From the relevant literature explain the Total Quality Management (TQM) processes the chosen organization follows and identify one quality challenge/issue that the organization faced or is currently facing. Explain how the organization managed/or still managing the particular quality challenge/issue. Critically analyze whether the organization failed or succeeded in achieving and maintaining quality performance. Provide a few critical recommendations for business managers in order to highlight the importance of Total Quality Management (TQM) within an organization.arrow_forward問題2 Production system design involves determining the arrangement of workstations and the... O allocation of resources to workstations design of the process O production schedule all of the abovearrow_forward
- Elaborate on the need for and the benefits of an effective supply chain management (SCM) system in the context of a globalized and networked economy. In your answer, explain how organizations like Dell and Hewlett-Packard leverage supply chain networks to maintain competitiveness, and analyse the impact of globalization, technological advancements, and business environment changes on supply chain structures. Additionally, evaluate the key components of SCM, including distribution network configuration, inventory management, and cash-flow management, and discuss how these components contribute to creating an effective and integrated supply chain. (15) 3.2. Critically evaluate the requirements for effective inventory management within an organization. In your answer, discuss the importance of inventory accounting systems, the role of cost information (holding, ordering, and shortage costs), and the significance of classification systems like ABC analysis. Additionally, analyse how…arrow_forwardAssess the role of EDI in ensuring supply chain security and data integrity. How does EDI contribute to reducing vulnerabilities in supply chain operations, and what best practices should organizations adopt to maintain a secure and reliable EDI system? (10) 1.3. Examine how the adoption of modern EDI systems influences the strategic decision-making process in supply chain management. How does EDI provide supply chain managers with actionable insights, and what are the implications of these insights for long-term supply chain planning? (10) 1.4. Evaluate the potential challenges and risks associated with the modernization of EDI systems in supply chain management. How can organizations effectively manage these challenges to ensure successful EDI implementation and ongoing optimization? (10)arrow_forwardAnalyse the impact of integrating EDI (Electronic Data Interchange) with API (Application Programming Interface) on supply chain management, particularly focusing on how this integration enhances information flow and operational efficiency. Consider the challenges that might arise from this integration in terms of managing legacy systems alongside modern applications.arrow_forward
- 1) View the video What is Operations Management (14.01 minutes, Ctrl+Click on the link); what are your key takeaways (tie to one or more of the topics discussed in Chapters 1 and/or 2) after watching this video. (https://www.viddler.com/embed/d01189e1) Note: As a rough guideline, please try to keep the written submission to one or two paragraphs. 2) View the video What McDonald’s is serving up at its new CosMc’s Chain (3.42 mins, Ctrl+Click in the link), and answer the following questions: (https://www.youtube.com/watch?v=k7ojpUzE8q4) i) From a strategic perspective, why do you think McDonald’s is opting for this new chain rather than trying to launch the new menu in its existing restaurants? ii) What factors do you think in McDonald’s external and internal environments are driving its decision to open the CosMc’s locations? iii) How do you think this format will improve McDonald’s profit margin as compared to its regular fast-food restaurants? Note: As a…arrow_forwardSince the end of World War II, globalization has steadily increased with rapid expansion around the turn of the 21st century. What are some of the forces driving globalization and international business? What are some of the challenges of engaging in international business compared to doing business in your home country?arrow_forwardPS.53 Brother I.D. Ricks is a faculty member at BYU-Idaho whose grandchildren live in Oklahoma and California. He and his wife would like to visit their grandchildren at least once a year in these states. They currently have one vehicle with well over 100,000 miles on it, so they want to buy a newer vehicle with fewer miles and that gets better gas mileage. They are considering two options: (1) a new subcompact car that would cost $18,750 to purchase or (2) a used sedan that would cost $12,750.They anticipate that the new subcompact would get 37 miles per gallon (combined highway and around town driving) while the sedan would get 26 miles per gallon. Based on their road tripping history they expect to drive 13,000 miles per year. For the purposes of their analysis they are assuming that gas will cost $2.93 per gallon.Question: How many miles would the Ricks need to drive before the cost of these two options would be the same? (Display your answer to the nearest whole number.) (Hint:…arrow_forward
- MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing
 Contemporary MarketingMarketingISBN:9780357033777Author:Louis E. Boone, David L. KurtzPublisher:Cengage Learning
Contemporary MarketingMarketingISBN:9780357033777Author:Louis E. Boone, David L. KurtzPublisher:Cengage Learning Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,  Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning
Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning





