Chapter 4, Problem 67QAP

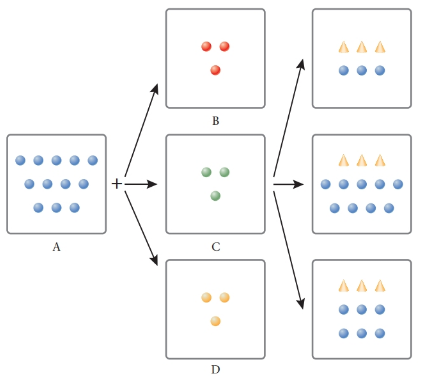
Consider four beakers. Beaker A has an aqueous solution of NaOH in which the OH^- ions are represented by blue circles. Beaker B has a weak acid; HX is represented by red circles. Beaker C has a weak acid; H₂X is represented by green circles. Beaker D has a weak acid; H₃X is represented by yellow circles. X^- ions are represented by triangles. Match the pictorial representations with the reactions given below.

(a) $\text{HX}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\to {\text{X}}^{-}\left(aq\right)+{\text{H}}_{\text{2}}\text{O}$(b) ${\text{H}}_{\text{2}}\text{X}\left(aq\right)+{\text{2OH}}^{-}\left(aq\right)\to {\text{X}}^{-}\left(aq\right)+{\text{2H}}_{\text{2}}\text{O}$(c) ${\text{H}}_{\text{3}}\text{X}\left(aq\right)+{\text{3OH}}^{-}\left(aq\right)\to {\text{X}}^{-}\left(\text{aq}\right)+{\text{3H}}_{\text{2}}\text{O}$