
Concept explainers
(a)
The equations of motion of the system shown in Figure P4.90.
Answer to Problem 4.90P
The equations of motion of the system given below,
Explanation of Solution
Given:
The masses are
The spring constant are
Concept used:
Newton’s Second law of motion and Hooke’s Law are used to obtain the equation of motions.
Figure P4.90
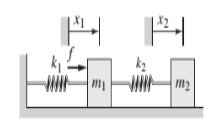
Calculation:
Free body diagram of
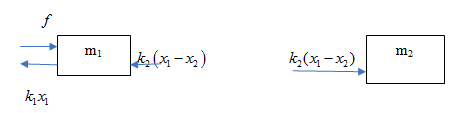
Applying Newton’s Second law of motion to mass m1
Substituting values for
Substituting values for
Therefore the equations of motion of the system given below,
Where,
(b)
The transfer functions for
Answer to Problem 4.90P
Explanation of Solution
Given:
From part (a),
Concept used:
Laplace Transformation used to obtain the transfer functions.
Assume zero initial conditions for
Calculation:
Converting the equations (1) and (2) to Laplace domain,
for zero initial condition,
from equation (6),
From equation (7) and (5),
From equation (7) and (6),
(c)
A plot of unit step responses of
Answer to Problem 4.90P
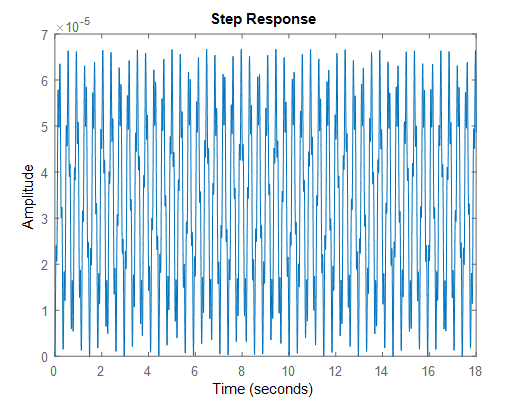
Explanation of Solution
Given:
unit-step response of
Solution:
Using MATLAB,
>>sys1=tf([1,0,1000],[20,0,11*10^4,0,3*10^7]);
>> step(sys1)
Want to see more full solutions like this?
Chapter 4 Solutions
System Dynamics
- Hydrodynamic Lubrication Theory Q1: Convert this equations into Python by 1- ah ap a h³ ap 1..ah = ax 12μ ax ay 12μ ay 2 ax Where P=P(x, y) is the oil film pressure. 2- 3μU (L² ε sin P= C²R (1+ cos 0)³ Q2: prove that |h(0) = C(1+ cos 0) ?arrow_forward### To make a conclusion for a report of an experiment on rockets, in which the openrocket software was used for the construction and modeling of two rockets: one one-stage and one two-stage. First rocket (single-stage) reached a maximum vertical speed of 200 m/s and a maximum height of 1000 m The second rocket (two-stage) reached a maximum vertical speed of 250 m/s and a maximum height of 1800 m To make a simplified conclusion, taking into account the efficiency of the software in the study of rocketsarrow_forwardWhat is the difference between saturated liquid and compressed liquid? What is the difference between the critical point and the triple pointarrow_forward
- What is quality? Does it have any meaning in the superheated vapour region? What is the difference between saturated vapor and superheated vapour? What is the difference between saturated liquid and compressed liquid? What is the difference between the critical point and the triple point?arrow_forwardHomework#5arrow_forwardDescribe the principle operation of PEMFC, and role of membrane electrode assembly (MEA).arrow_forward
- Homework#5arrow_forwardUsing graphical methods, draw the pressure angle at the position shown in (a) and (b). e |------- R = Cam Base Radius e = Follower Offset ẞ₁ = Section Duration 1 B₁ = Section Duration 2 ẞ₂ = Section Duration 3 В2 B₁ Follower Position ww R ẞ3 (a) Reference Radial (b)arrow_forwardThe figure below illustrates a graph that has a variable load torque and constant drive torque. Each cycle lasts three revolutions (6л radians). Torque (N-m) 600 550 400 1 200 TD= 225 N-m 2 + -T₁ 3 4 1 + 0 In addition, the rotation speed is @o steady-state conditions, determine 1. the average power required, 2πT 4π 5πT 6п Ꮎ = 180° rpm = 18.85 rad/sec, Imachine 125 kg-m². Assuming 2. the maximum and minimum rotational speeds throughout a cycle, 3. the mass of a 0.6-meter-diameter solid disc flywheel to produce Cs = 0.025.arrow_forward
- An elastic cord is stretched between 2 points A and B located 2y = 0.8 m apart in the horizontal plane. When stretched directly between A and B, the tension is P₂ = 40 N. The cord is then stretched as shown until its midpoint C has moved through x = 0.3 m to C', and a force of F = 240 N is required to hold the cord at C'. A pellet (m = 0.1 kg) is placed at C' and the cord is released. Find the speed of the pellet as it passes through C.arrow_forwardA 6305 ball bearing is subjected to a steady 5000-N radial load and a 2000-N thrust load and uses a very clean lubricant throughout its life. If the inner race angular velocity is 500rpm find (a) The equivalent radial load (b) The L10 life (c) The L50 lifearrow_forwardSlove this the question plearrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





