
A stream containing H2S and inert gases and a second stream of pure SO2 are fed to a sulfur recover)' reactor, where the reaction
2H2S + SO2 -» 3S + 2H2O
takes place. The feed rates are adjusted so that the ratio of H2S to SO2 in the combined feed is always stoichiometric.
In the normal operation of the reactor the flow rate and composition of the H2S feed stream both fluctuate. In the past, each time either variable changed the required SO2 feed rate had to be reset by adjusting a valve in the feed line. A control system has been installed to automate this process. The H2S feed stream passes through an electronic flowmeter that transmits a signal Rf directly proportional to the molar flow rate of the stream, h{. When = 100 kmol/h, the transmitted signal R(= 15 mV. The mole fraction of H2S in this stream is measured with a thermal conductivity detector, which transmits a signal /fa. Analyzer calibration data are as follows:
| fla(mV) | 0 | 25.4 | 42.8 | 58.0 | 71.9 | 85.1 |
| x(mol H2S/mol) | 0.00 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
The controller takes as input the transmitted values of Rf and R3and calculates and transmits a voltage signal j?c to a flow control valve in the SO2 line, which opens and closes to an extent dependent on the value of Rc. A plot of the SO2 flow rate. fic, versus Rcon rectangular coordinates is a straight line through the points (Rc= 10.0mV.hc= 25.0kmol/h) and (/<. = 25.0mV.hc = 60.0kmol/h).
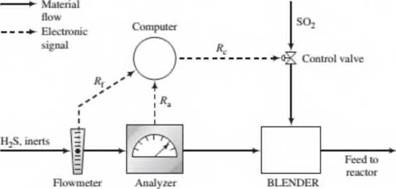
- Why would it be important to feed the reactants in stoichiometric proportion? (Hint: SO2 and especially H2S are serious pollutants.) What are several likely reasons for wanting to automate the SO2 feed rate adjustment?
- If the first stream contains 85.0 mole% H2S and enters the unit at a rate of hf = 3.00 X 102 kmol/h, what must the value of nt(kmol SO2/h) be?
- Fit a function to the H2S analyzer calibration data to derive an expression for x as a function of Rt. Check the fit by plotting both the function and the calibration data on the same graph.
- Derive a formula for Rcfrom specified values of Rf and Ra, using the result of Part (c) in the derivation. (This formula would be built into the controller.) Test the formula using the flow rate and composition data of Part (a).
- The system has been installed and made operational, and at some point the concentration of H2S in the feed stream suddenly changes. A sample of the blended gas is collected and analyzed a short time later and the mole ratio of H2S to SO2 is not the required 2:1. List as many possible reasons as you can think of for this apparent failure of the control system.
Trending nowThis is a popular solution!

Chapter 4 Solutions
EBK ELEMENTARY PRINCIPLES OF CHEMICAL P
Additional Science Textbook Solutions
Web Development and Design Foundations with HTML5 (8th Edition)
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Modern Database Management
Starting Out With Visual Basic (8th Edition)
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
- Can you provide me the answer of these pleasearrow_forwardA constant-volume process involving 2.0 moles of diatomic ideal gas, for which cV = (5/2)R, is at an initial state of 111 kPa and 277 K and is then heated reversibly to 356 K. Calculate the P2 (kPa), dU (kJ), heat transfer q (kJ mol–1), and w (kJ mol–1).arrow_forwardProblem 1 Marks: 60 Section: 1a): 30 marks, Section 1b):30 marks A laboratory scale fluidized bed is considered for studying a catalytic ozone decomposition. a) It is requested to derive model equations under the following assumptions: ■ Operation of the catalytic reactor under steady state conditions, There is no influence of thermal ozone decomposition reactions. The fluidized bed includes bubbles and dense phase. □ The dense phase can be simulated using a CSTR The fluidized bed bubbles contain catalyst particles and can be simulated as a DSTR (batch). □ The jets contain particles and can be simulated with a PFR. The influence of the freeboard has to be considered using a PFR model. The available catalytic reaction rate model is r (moles/gcat.s)= -k CA b) Same than on a) under unsteady state conditions, using an absorbable and reactive tracer. Note: A step-by step derivation of the model equations is required here. A quick answer will not do. Problem 2 Marks: 40 Section 2a: 30 marks,…arrow_forward
- Penicillin process Penicillium chrysogenum is used to produce penicillin in a 90,000-litre fermenter. The volumetric rate of oxygen uptake by the cells ranges from 0.45 to 0.85 mmol l^−1 min^−1 depending on time during the culture. Power input by stirring is 2.9 W l^−1. Estimate the cooling requirements.arrow_forwardProduction of bakers’ yeast Bakers’ yeast is produced in a 50,000-litre fermenter under aerobic conditions. The carbon substrate is sucrose; ammonia is provided as the nitrogen source. The average biomass composition is CH_1.83O_0.55N_0.17 with 5% ash. Under conditions supporting efficient growth, biomass is the only major product and the biomass yield from sucrose is 0.5 g g^−1. If the specific growth rate is 0.45 h^−1, estimate the rate of heat removal required to maintain constant temperature in the fermenter when the yeast concentration is 10 g l^−1.arrow_forwardSensible energy change Calculate the enthalpy change associated with the following processes:(a) m-Cresol is heated from 25°C to 100°C(b) Ethylene glycol is cooled from 20°C to 10°C(c) Succinic acid is heated from 15°C to 120°C(d) Air is cooled from 150°C to 65°Carrow_forward
- ▼ Enzyme conversion An immobilised enzyme process is used in an ice-cream factory to hydrolyse lactose (C12H22O11) to glucose (C6H12O6) and galactose (C6H1206): C12H22O11 + H2O →→ C6H12O + C6H12O6 Gel beads containing ß-galactosidase are packed into a column reactor; 2500 kg of lactose enters the reactor per day as a 10% solution in water at 25°C. The reactor operates at steady state and 32°C; all of the lactose is converted. Because the heat of reaction for enzyme conversions is not as great as for cell culture, sensible heat changes and heats of mixing cannot be ignored. Lactose Water Ah (kJ gmol¹) C, (cal g¹ ºC-¹) Ahm (kcal gmol¹) 3.7 -5652.5 0.30 1.0 Glucose -2805.0 0.30 5.6 Galactose -2805.7 0.30 5.6 (a) What is the standard heat of reaction for this enzyme conversion? (b) Estimate the heating or cooling requirements for this process. State explicitly whether heating or cooling is needed.arrow_forwardBacterial production of alginate Azotobacter vinelandii is investigated for production of alginate from sucrose. In a continuous fermenter at 28°C with ammonia as nitrogen source, the yield of alginate was found to be 4 g g^−1 oxygen consumed. It is planned to produce alginate at a rate of 5 kg h^−1. Since the viscosity of alginate in aqueous solution is considerable, energy input due to mixing the broth cannot be neglected. The fermenter is equipped with a flat-blade disc turbine; at a satisfactory mixing speed and air flow rate, the power requirements are estimated at 1.5 kW. Calculate the cooling requirements.arrow_forwardPreheating nutrient medium Steam is used to heat nutrient medium in a continuous-flow process. Saturated steam at 150°C enters a coil on the outside of the heating vessel and is completely condensed. Liquid medium enters the vessel at 15°C and leaves at 44°C. Heat losses from the jacket to the surroundings are estimated as 0.22 kW. If the flow rate of medium is 3250 kg h^−1 and its heat capacity is 0.9 cal g^−1 °C^−1, how much steam is required?arrow_forward
- Q3] Determine the optimal operating conditions (XA, t, and CR) in a mixed flow reactor to maximize the concentration of R (CR) in the effluent, where an aqueous feed A with an initial concentration of CA0-40 mol/m³ enters the reactor, undergoes decomposition, and exits as a mixture containing A, R, and S. K₁ AR, FR = k₁C, k₁ = 0.4 m³/(mol min) SA AS, rs = k₂CA, k₂ = 2(min), CA0 = 40 mol/m³arrow_forwardConsider the parallel decomposition of A of different orders with FR = 1, rs = 2CA and IT = C. Determine the maximum concentration of desired product obtainable in mixed flow reactor and plug flow reactor. (1) R is desired product and CA0 = 2. (2) S is desired product and CA0 = 4. R S Tarrow_forward1. Copper is known to be toxic to fish, and in particular, the free ion Cu²+ species typically shows greatest toxicity. a. Calculate the speciation of Cu(II) for freshwater at a pH value of 8.3 as the hardness increases from 20 (soft) to 100 (moderately hard) to 200 (very hard) mg/L as CaCO3. Assume that the total divalent Cu(II) concentration is 10 µg/L. b. Based on your findings in part (a), do you think it is appropriate to set a single regulatory limit or should it depend on variables such as pH and hardness? Explain your answer.arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





