Chapter 4, Problem 4.43P

Interpretation Introduction

Interpretation:

The applied stress needed to cause the slip to begin in the $\left[111\right]$ direction on the $\left(110\right),\left(011\right)$, and $\left[10\overline{1}\right]$ slip planes needs to be calculated.

Concept Introduction:

The angle between the normal to the slip plane and the applied force can be calculated as follows:

  $\cos \varphi =\frac{a.b}{\left|ab\right|}$

Here, $a,b$ are the planes and the angle between the normal to the slip plane and the applied force is $\varphi$.

Answer to Problem 4.43P

The applied stress that causes the slip on the plane $\left[110\right]\text{is }\left[\infty \right]$.

The applied stress that causes the slip on the plane $\left[011\right]\text{ is }\left[29412psi\right]$.

The applied stress that causes the slip on the plane $\left[10\overline{1}\right]\text{ is }\left[29412psi\right]$.

Explanation of Solution

The angle between the normal to the slip plane and the applied force can be calculated as follows:

  $\cos \varphi =\frac{a.b}{\left|ab\right|}$

Here, $a,b$ are the planes and the angle between the normal to the slip plane and the applied force is $\varphi$.

Substitute $\left[001\right]$ for a and $\left[1\overline{1}1\right]\text{ for }b$.

  $\begin{array}{c}\cos \varphi =\frac{\left[001\right].\left[1\overline{1}1\right]}{\sqrt{0^2+0^2+1^2}\times \sqrt{1^2+{\left(-1\right)}^2+1^2}}\\ =\frac{\left(0\times 1\right)+\left(0\times -1\right)+\left(1\times 1\right)}{1\times \sqrt{3}}\\ \cos \varphi =\left(\frac{1}{\sqrt{3}}\right)\\ \varphi ={\cos }^{-1}\left(0.577\right)\\ ={54.76}^{\text{o}}\end{array}$

The angle between the slip direction and the applied force slip plane $\left[110\right]$ can be calculated as follows:

  $\cos {\lambda }_1=\frac{a.c}{\left|ac\right|}$

Here, $a,c$ are the planes and the angel between the slip direction and the applied force slip plane $\left[110\right]\text{ is }{\lambda }_1$.

Substitute $\left[001\right]\text{ for a and }\left[110\right]\text{ for }c$

  $\begin{array}{c}\cos {\lambda }_1=\frac{\left[001\right].\left[110\right]}{\sqrt{0^2+0^2+1^2}\times \sqrt{1^2+1^2+0^2}}\\ =\frac{\left(0\times 1\right)+\left(0\times 1\right)+\left(1\times 0\right)}{1\times \sqrt{2}}\\ \cos {\lambda }_1=\left(0\right)\\ {\lambda }_1={\cos }^{-1}\left(0\right)\\ ={90}^{\text{o}}\end{array}$

Calculate the angel between the slip direction and the applied force slip plane $\left[011\right]$

  $\cos {\lambda }_2=\frac{a.d}{\left|ad\right|}$

Here, $a,d$ are the planes and the angel between the slip direction and the applied force slip plane $\left[110\right]\text{ is }{\lambda }_1$.

Substitute $\left[001\right]\text{ for a and }\left[011\right]\text{ for d}$

  $\begin{array}{c}\cos {\lambda }_2=\frac{\left[001\right].\left[011\right]}{\sqrt{0^2+0^2+1^2}\times \sqrt{0^2+1^2+1^2}}\\ =\frac{\left(0\times 1\right)+\left(0\times 1\right)+\left(1\times 1\right)}{1\times \sqrt{2}}\\ \cos {\lambda }_2=\left(\frac{1}{\sqrt{2}}\right)\\ {\lambda }_2={\cos }^{-1}\left(\frac{1}{\sqrt{2}}\right)\\ ={45}^{\text{o}}\end{array}$

The angle between the slip direction and the applied force slip plane $\left[10\overline{1}\right]$ can be calculated as follows:

  $\cos {\lambda }_3=\frac{a.e}{\left|ae\right|}$

Here, $a,e$ are the planes.

Substitute $\left[001\right]\text{ for a and }\left[10\overline{1}\right]\text{ for e}$

  $\begin{array}{c}\cos {\lambda }_3=\frac{\left[001\right].\left[10\overline{1}\right]}{\sqrt{0^2+0^2+1^2}\times \sqrt{{\left(1\right)}^2+0^2+{\left(-1\right)}^2}}\\ =\frac{\left|\left(0\times 1\right)+\left(0\times 0\right)+\left(1\times -1\right)\right|}{1\times \sqrt{2}}\\ \cos {\lambda }_3=\left(\frac{1}{\sqrt{2}}\right)\\ {\lambda }_3={\cos }^{-1}\left(\frac{1}{\sqrt{2}}\right)\\ ={45}^{\text{o}}\end{array}$

The cubic crystal system that represents the orientation of different planes is as follows:

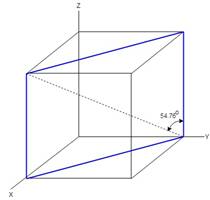
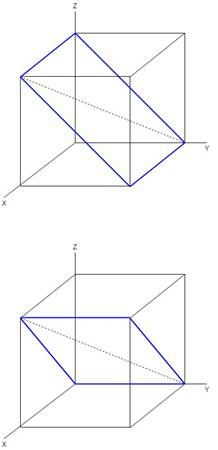
The applied stress produces resolved shear stress, ${\tau }_r$ which is equal to the critical shear stress, ${\tau }_{crss}$. Hence,

  ${\tau }_r={\tau }_{crss}$

Apply Schmidt's law and calculate the applied stress that causes the slip on the plane $\left[110\right]$ as follows.

  ${\tau }_{crss}={\sigma }_1\cos {\lambda }_1\cos \varphi$

Substitute $12,000psi$ for ${\tau }_{crss},{54.76}^{\text{o}}\text{ for }\varphi$, and ${90}^{\text{o}}\text{ for }{\lambda }_1$.

  $\begin{array}{c}12,000={\sigma }_1\times \cos {90}^{\text{o}}\times \cos {54.76}^{\text{o}}\\ {\sigma }_1=\frac{12,000}{\cos {90}^{\text{o}}\times \cos {54.76}^{\text{o}}}\\ =\frac{12,000}{0}\\ =\infty \end{array}$

Therefore, the applied stress that causes the slip on the plane $\left[110\right]$ is $\left[\infty \right]$.

Apply Schmidt's law and calculate the applied stress that causes the slip on the plane $\left[011\right]$ as follows.

  ${\tau }_{crss}={\sigma }_2\cos {\lambda }_2\cos \varphi$

Substitute $12,000psi$ for ${\tau }_{crss},{54.76}^{\text{o}}\text{ for }\varphi$, and ${45}^{\text{o}}\text{ for }{\lambda }_2$.

  $\begin{array}{c}12,000={\sigma }_2\times \cos {45}^{\text{o}}\times \cos {54.76}^{\text{o}}\\ {\sigma }_2=\frac{12,000}{\cos {45}^{\text{o}}\times \cos {54.76}^{\text{o}}}\\ =\frac{12,000}{0.408}\\ =29412psi\end{array}$

Therefore, the applied stress that causes the slip on the plane $\left[011\right]\text{ is }\left[29412psi\right]$.

Conclusion

The applied stress that causes the slip on the plane $\left[110\right]\text{is }\left[\infty \right]$.

The applied stress that causes the slip on the plane $\left[011\right]\text{ is }\left[29412psi\right]$.

The applied stress that causes the slip on the plane $\left[10\overline{1}\right]\text{ is }\left[29412psi\right]$.