Chapter 4, Problem 4.114RP

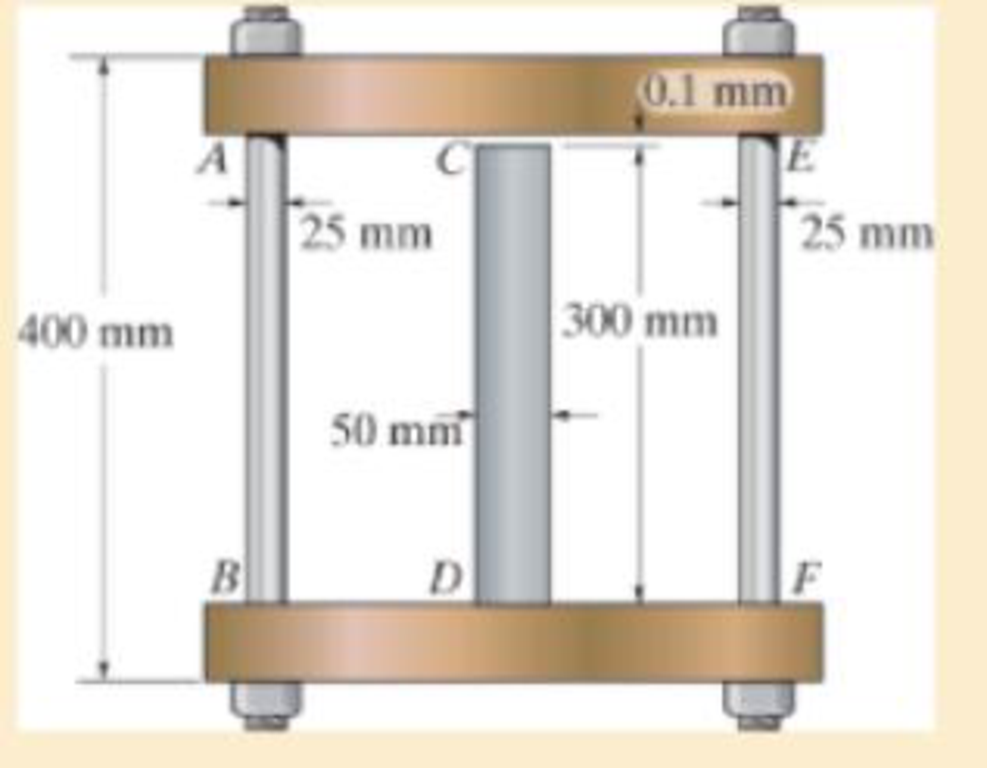
The assembly consists of two A992 steel bolts AB and EF and an 6061-T6 aluminum rod CD. When the temperature is at 30° C, the gap between the rod and rigid member AE is 0.1 mm Determine the normal stress developed in the bolts and the rod if the temperature rises to 130° C.

Assume BF is also rigid.

R4–1/2

To determine

The normal stress developed in the bolts and rod.

Answer to Problem 4.114RP

The normal stress developed in the bolts and rod are $\underset{\_}{33.5\text{MPa}}$ and $\underset{\_}{16.8\text{MPa}}$

Explanation of Solution

Given information:

The two bolts AB and EF are made of A992 steel.

The rod CD is made of 6061-T6 aluminum.

The Young’s modulus of the steel is $\left(E_{st}\right)$ $200\times {10}^3{\text{N/mm}}^2$

The Young’s modulus of the aluminum $\left(E_{al}\right)$ is $68.9\times {10}^3{\text{N/mm}}^2$

The coefficient of thermal expansion of the steel $\left({\alpha }_{st}\right)$ is $12\times {10}^{-6}\text{m/m}°\text{C}$

The coefficient of thermal expansion of the aluminum $\left({\alpha }_{al}\right)$ is $24\times {10}^{-6}\text{m/m}°\text{C}$

The initial temperature $\left(T_1\right)$ is $30°\text{C}$

The finial temperature $\left(T_2\right)$ is $130°\text{C}$

The gap between the rod and rigid member AE is $0.1\text{mm}$

The diameter of the bolts AB and EF $\left(d_b\right)$ is $25\text{mm}$

The diameter of the rod CD $\left(d_r\right)$ is $50\text{mm}$

The length of the bolts AB and EF $\left(L_b\right)$  is $400\text{mm}$

The length of the rod CD $\left(L_r\right)$ is $300\text{mm}$

Calculation:

Calculate the area of the bolts AB and EF $\left(A_b\right)$ using the formula:

$A_b=\frac{\pi }{4}{d}_b^2$ (1)

Substitute $25\text{mm}$ for $d_b$ in Equation (1).

$\begin{array}{c}{A}_b=\frac{\pi }{4}\times {25}^2\\ =490.874{\text{mm}}^2\end{array}$

Calculate the area of the rod CD $\left(A_r\right)$ using the formula:

$A_r=\frac{\pi }{4}{d}_r^2$ (2)

Substitute $50\text{mm}$ for $d_r$ in Equation (2).

$\begin{array}{c}{A}_r=\frac{\pi }{4}\times {50}^2\\ =1,963.495{\text{mm}}^2\end{array}$

Calculate the difference of temperature $\left(\Delta T\right)$ using the formula:

$\Delta T=T_2-T_1$ (3)

Substitute $30°\text{C}$ for $T_1$ and $130°\text{C}$ for $T_2$ in Equation (3).

$\begin{array}{c}\Delta T=130-30\\ =100°\text{C}\end{array}$

Show the free body diagram of the rigid cap as in Figure 1.

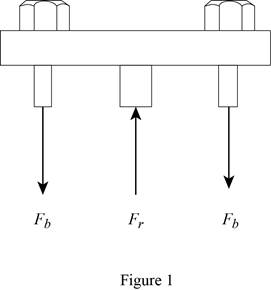
Refer Figure 1.

Calculate the vertical forces by applying the equation of equilibrium:

Sum of vertical forces is equal to 0.

$\begin{array}{l}{\displaystyle \sum F_y}=0\\ -F_b+F_r-F_b=0\\ F_r-2F_b=0\\ F_r=2F_b\end{array}$ (4)

Here, $F_b$ is force at the bolts AB and EF and $F_r$ is force at the rod CD.

Show the initial and final position of the assembly as in Figure 2.

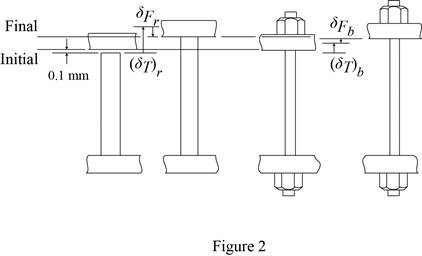
Refer Figure 2.

Here ${\left({\delta }_T\right)}_r$ is deformation at rod due to temperature, ${\left({\delta }_T\right)}_b$ is deformation at bolts due to temperature, ${\left({\delta }_F\right)}_r$ is deformation at rod due to force, and ${\left({\delta }_F\right)}_b$ is deformation at bolts due to force.

The deformation is as follows:

$\begin{array}{l}{\left({\delta }_T\right)}_r-{\left({\delta }_F\right)}_r-0.1={\left({\delta }_T\right)}_b+{\left({\delta }_F\right)}_b\\ {\alpha }_{al}\Delta T{L}_r-\frac{F_r{L}_r}{A_r{E}_{al}}-0.1={\alpha }_{st}\Delta T{L}_b+\frac{F_b{L}_b}{A_b{E}_{st}}\end{array}$ (5)

Substitute $24\times {10}^{-6}\text{m/m}°\text{C}$ for ${\sigma }_{al}$, $12\times {10}^{-6}\text{m/m}°\text{C}$ for ${\alpha }_{st}$, $100°\text{C}$ for $\Delta T$, $300\text{mm}$ for $L_r$, $400\text{mm}$ for $L_b$, $1,963.495{\text{mm}}^2$ for $A_r$, $490.874{\text{mm}}^2$ for $A_b$, $68.9\times {10}^3{\text{N/mm}}^2$ for $E_{al}$, and $200\times {10}^3{\text{N/mm}}^2$ for $E_{st}$ in Equation (5).

$\begin{array}{l}\left[\begin{array}{l}\left(24\times {10}^{-6}\times 100\times 300\right)-\\ \frac{F_r\times 300}{1,963.495\times 68.9\times {10}^3}-0.1\end{array}\right]=\left[\begin{array}{l}\left(12\times {10}^{-6}\times 100\times 400\right)+\\ \frac{F_b\times 400}{490.874\times 200\times {10}^3}\end{array}\right]\\ 0.72-2.2175\times {10}^{-6}{F}_r-0.1=0.48+4.0743\times {10}^{-6}{F}_b\\ 4.0743\times {10}^{-6}{F}_b+2.2175\times {10}^{-6}{F}_r=0.72-0.1-0.48\end{array}$

$\begin{array}{l}4.0743\times {10}^{-6}{F}_b+2.2175\times {10}^{-6}{F}_r=0.14\\ F_b+0.5443F_r=34,361.73\end{array}$ (6)

Calculate the force at the bolts AB and EF $\left(F_b\right)$

Substitute $2F_b$ for $F_r$ in Equation (6).

$\begin{array}{l}{F}_b+0.5443\left(2F_b\right)=34,361.73\\ 2.0886F_b=34,361.73\\ F_b=\frac{34,361.73}{2.0886}\\ F_b=16,452\text{N}\end{array}$

Calculate the force at the rod CD $\left(F_r\right)$

Substitute $16,452\text{N}$ for $F_b$ in Equation (4).

$\begin{array}{c}{F}_r=2\left(16,452\right)\\ =32,904\text{N}\end{array}$

Calculate the normal stress developed in the bolts AB and EF $\left({\sigma }_b\right)$ using the formula:

${\sigma }_b=\frac{F_b}{A_b}$ (7)

Substitute $16,452\text{N}$ for $F_b$ and $490.874{\text{mm}}^2$ for $A_b$ in Equation (7).

$\begin{array}{c}{\sigma }_b=\frac{16,452}{490.874}\\ =33.5{\text{N/mm}}^2\times \frac{1\text{MPa}}{1{\text{N/mm}}^2}\\ =33.5\text{MPa}\end{array}$

Calculate the normal stress developed in the rod CD $\left({\sigma }_r\right)$ using the formula:

${\sigma }_r=\frac{F_r}{A_r}$ (8)

Substitute $32,904\text{N}$ for $F_b$ and $1,963.495{\text{mm}}^2$ for $A_r$ in Equation (8).

$\begin{array}{c}{\sigma }_r=\frac{3,2904}{1,963.495}\\ =16.8{\text{N/mm}}^2\times \frac{1\text{MPa}}{1{\text{N/mm}}^2}\\ =16.8\text{MPa}\end{array}$

Hence, the normal stress developed in the bolts and rod are $\underset{\_}{33.5\text{MPa}}$ and $\underset{\_}{16.8\text{MPa}}$