Chapter 3.9, Problem 98E

Logistic growth Scientists often use the logistic growth function $P(t)=\frac{P_{0}K}{P_0+(K-P_0)e^{-r_{0}t}}$to model population growth, where P₀ is the initial population at time t = 0, K is the carrying capacity, and r₀ is the base growth rate. The carrying capacity is a theoretical upper bound on the total population that the surrounding environment can support. The figure shows the sigmoid (S-shaped) curve associated with a typical logistic model.

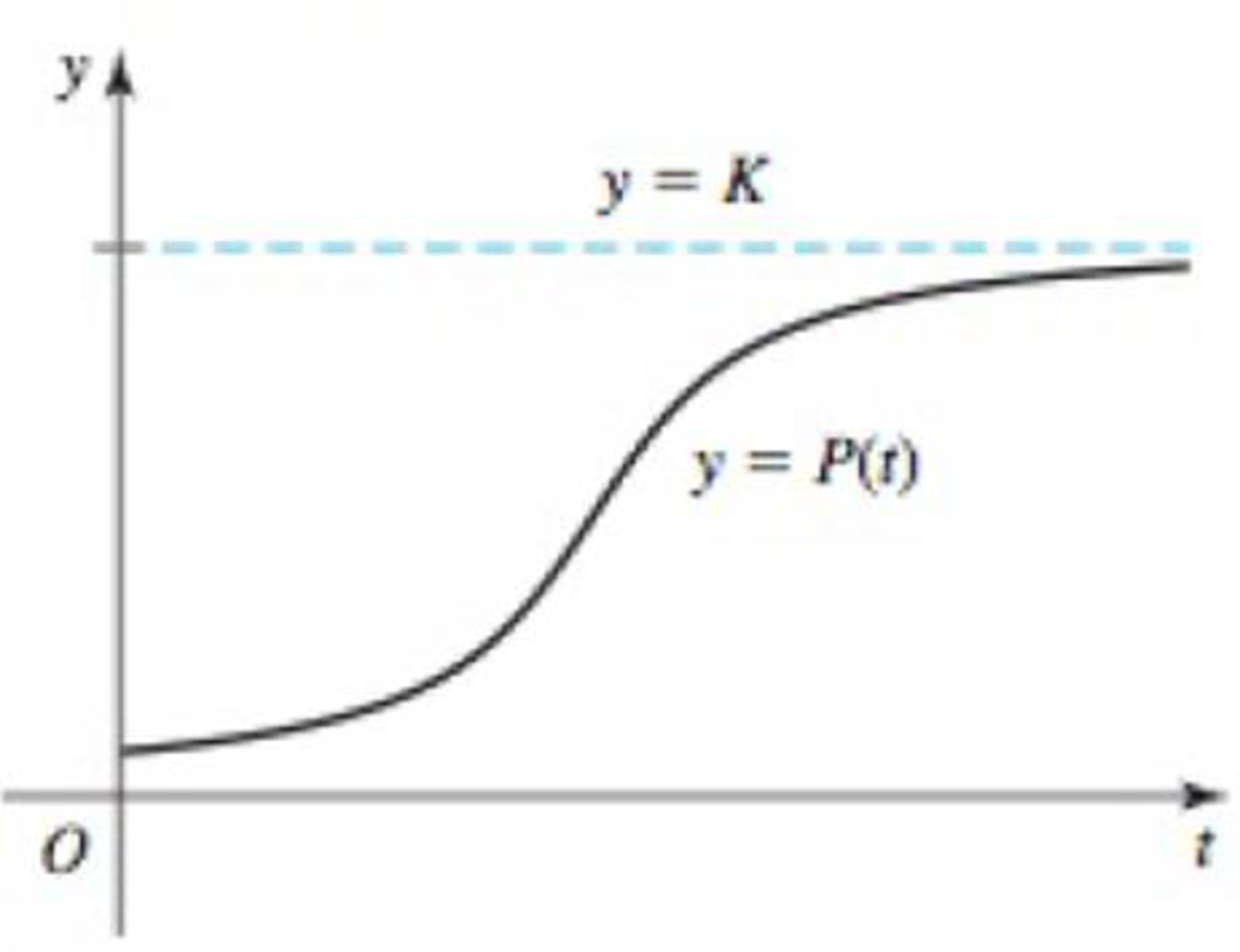
94. World population (part 1) The population of the world reached 6 billion in 1999 (t = 0). Assume Earth’s carrying capacity is 15 billion and the base growth rate is r₀ = 0.025 per year.

1. a. Write a logistic growth function for the world’s population (in billions) and graph your equation on the interval 0 ≤ t ≤ 200 using a graphing utility.
2. b. What will the population be in the year 2020? When will it reach 12 billion?