Chapter 3.8, Problem 35E

(a)

To determine

To find: The type of variation that describes the relationship between torque, mass and distance. Explain.

Answer to Problem 35E

  $\begin{array}{l}T=KMD\\ T\text{ varies jointly as }D\text{ and }M\end{array}$

Explanation of Solution

Given information: Physics: If you have observed people on a seesaw, you may have noticed that the heavier person must sit closer to the fulcrum for the seesaw to balance. In doing so, the heavier participant creates a rotational force, called torque. The torque on the end of a seesaw depends on the mass of the person and his or her distance from the seesaw’s fulcrum. In order to reduce torque, one must either reduce the distance between the person and the fulcrum or replace the person with someone having a smaller mass.

  

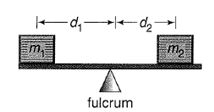
Calculation:

T varies jointly as D and M

  $\begin{array}{l}M=\text{mass}\\ D=\text{distance}\\ T=\text{torque}\\ T=KMD\end{array}$

(b)

To determine

To derive: An equation that represents this seesaw in balance, if $m_1,d_1\text{ and }{T}_1$ be the mass, distance and torque on one side of a seesaw and let $m_2,d_2\text{ and }{T}_2$ be the mass, distance and torque on the other side.

Answer to Problem 35E

  $F=\left(\text{mass}\right)\left(\text{distance from fulcrum}\right)$

Explanation of Solution

Given information: Physics: If you have observed people on a seesaw, you may have noticed that the heavier person must sit closer to the fulcrum for the seesaw to balance. In doing so, the heavier participant creates a rotational force, called torque. The torque on the end of a seesaw depends on the mass of the person and his or her distance from the seesaw’s fulcrum. In order to reduce torque, one must either reduce the distance between the person and the fulcrum or replace the person with someone having a smaller mass.

  

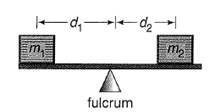
Calculation:

In order for the seesaw to be in balance, the Force on the left side must equal the force on the other side.

F = (mass) (distance from fulcrum)

  $F_1=F_2$

  $75\left(3.3m\right)=125\left(x\right)$

  $x=1.98\text{ m}$

(c)

To determine

To find: The distance the babysitter should sit from the pivot in order to balance the seesaw using the equation found in part b, is a 75-pound child and a 125-pound babysitter sit at either end of a seesaw. The child sits 3.3 meters from the fulcrum.

Answer to Problem 35E

  $\text{Distance}=1.98\text{ meters}$

Explanation of Solution

Given information: Physics: If you have observed people on a seesaw, you may have noticed that the heavier person must sit closer to the fulcrum for the seesaw to balance. In doing so, the heavier participant creates a rotational force, called torque. The torque on the end of a seesaw depends on the mass of the person and his or her distance from the seesaw’s fulcrum. In order to reduce torque, one must either reduce the distance between the person and the fulcrum or replace the person with someone having a smaller mass.

  

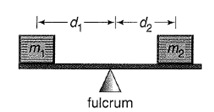
Calculation:

T varies jointly as D and M

  $\begin{array}{l}M=\text{mass}\\ D=\text{distance}\\ T=\text{torque}\\ T=KMD\end{array}$

Replace the values of T, K, M in the equation to find distance D

  $\begin{array}{l}\left(75\right)\left(3.3\right)=125\left(D\right)\\ 297.5=125\left(D\right)\\ D=1.98\text{ meters}\end{array}$