McDougal Littell Jurgensen Geometry: Student Edition Geometry

5th Edition

ISBN: 9780395977279

Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen

Publisher: Houghton Mifflin Company College Division

See similar textbooks

Videos

Question

Chapter 3.6, Problem 5CE

To determine

To tell: Whether the reasoning process “John knows that multiplying a number by 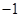merely changes the sign of the number. He reasons that multiplying a number by an even power of will change the sign of the number an even number of times. He concludes that this is equivalent to multiplying a number by so that every even power of 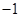is equal to 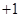is deductive or inductive.

Expert Solution & Answer

Answer to Problem 5CE

The reasoning process is deductive.

Explanation of Solution

Given information: “John knows that multiplying a number by 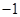McDougal Littell Jurgensen Geometry: Student Edition Geometry, Chapter 3.6, Problem 5CE , additional homework tip 6 merely changes the sign of the number. He reasons that multiplying a number by an even power of 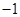will change the sign of the number an even number of times. He concludes that this is equivalent to multiplying a number by 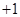McDougal Littell Jurgensen Geometry: Student Edition Geometry, Chapter 3.6, Problem 5CE , additional homework tip 8 so that every even power of 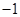is equal to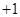

From the given statement, it is cleared that the conclusion based on definition.

That is, the conclusion based on accepted statement.

Thus, this conclusion must be true if hypothesis are true.

Therefore, the reasoning process is deductive.

Chapter 3.6, Problem 4CE

Chapter 3.6, Problem 6CE

Chapter 3 Solutions

McDougal Littell Jurgensen Geometry: Student Edition Geometry

Ch. 3.1 - Prob. 1CE Ch. 3.1 - Prob. 2CE Ch. 3.1 - Prob. 3CE Ch. 3.1 - Prob. 4CE Ch. 3.1 - Prob. 5CE Ch. 3.1 - Prob. 6CE Ch. 3.1 - Prob. 7CE Ch. 3.1 - Prob. 8CE Ch. 3.1 - Prob. 9CE Ch. 3.1 - Prob. 10CE

Ch. 3.1 - Prob. 11CE Ch. 3.1 - Prob. 12CE Ch. 3.1 - Prob. 13CE Ch. 3.1 - Prob. 14CE Ch. 3.1 - Prob. 15CE Ch. 3.1 - Prob. 16CE Ch. 3.1 - Prob. 17CE Ch. 3.1 - Prob. 18CE Ch. 3.1 - Prob. 19CE Ch. 3.1 - Prob. 1WE Ch. 3.1 - Prob. 2WE Ch. 3.1 - Prob. 3WE Ch. 3.1 - Prob. 4WE Ch. 3.1 - Prob. 5WE Ch. 3.1 - Prob. 6WE Ch. 3.1 - Prob. 7WE Ch. 3.1 - Prob. 8WE Ch. 3.1 - Prob. 9WE Ch. 3.1 - Prob. 10WE Ch. 3.1 - Prob. 11WE Ch. 3.1 - Prob. 12WE Ch. 3.1 - Prob. 13WE Ch. 3.1 - Prob. 14WE Ch. 3.1 - Prob. 15WE Ch. 3.1 - Prob. 16WE Ch. 3.1 - Prob. 17WE Ch. 3.1 - Prob. 18WE Ch. 3.1 - Prob. 19WE Ch. 3.1 - Prob. 20WE Ch. 3.1 - Prob. 21WE Ch. 3.1 - Prob. 22WE Ch. 3.1 - Prob. 23WE Ch. 3.1 - Prob. 24WE Ch. 3.1 - Prob. 25WE Ch. 3.1 - Prob. 26WE Ch. 3.1 - Prob. 27WE Ch. 3.1 - Prob. 28WE Ch. 3.1 - Prob. 29WE Ch. 3.1 - Prob. 30WE Ch. 3.1 - Prob. 31WE Ch. 3.1 - Prob. 32WE Ch. 3.1 - Prob. 33WE Ch. 3.1 - Prob. 34WE Ch. 3.1 - Prob. 35WE Ch. 3.1 - Prob. 36WE Ch. 3.1 - Prob. 37WE Ch. 3.1 - Prob. 38WE Ch. 3.1 - Prob. 39WE Ch. 3.1 - Prob. 40WE Ch. 3.1 - Prob. 41WE Ch. 3.1 - Prob. 42WE Ch. 3.2 - Prob. 1CE Ch. 3.2 - Prob. 2CE Ch. 3.2 - Prob. 3CE Ch. 3.2 - Prob. 4CE Ch. 3.2 - Prob. 5CE Ch. 3.2 - Prob. 6CE Ch. 3.2 - Prob. 7CE Ch. 3.2 - Prob. 8CE Ch. 3.2 - Prob. 9CE Ch. 3.2 - Prob. 10CE Ch. 3.2 - Prob. 11CE Ch. 3.2 - Prob. 12CE Ch. 3.2 - Prob. 13CE Ch. 3.2 - Prob. 14CE Ch. 3.2 - Prob. 1WE Ch. 3.2 - Prob. 2WE Ch. 3.2 - Prob. 3WE Ch. 3.2 - Prob. 4WE Ch. 3.2 - Prob. 5WE Ch. 3.2 - Prob. 6WE Ch. 3.2 - Prob. 7WE Ch. 3.2 - Prob. 8WE Ch. 3.2 - Prob. 9WE Ch. 3.2 - Prob. 10WE Ch. 3.2 - Prob. 11WE Ch. 3.2 - Prob. 12WE Ch. 3.2 - Prob. 13WE Ch. 3.2 - Prob. 14WE Ch. 3.2 - Prob. 15WE Ch. 3.2 - Prob. 16WE Ch. 3.2 - Prob. 17WE Ch. 3.2 - Prob. 18WE Ch. 3.2 - Prob. 19WE Ch. 3.2 - Prob. 20WE Ch. 3.2 - Prob. 21WE Ch. 3.2 - Prob. 22WE Ch. 3.2 - Prob. 23WE Ch. 3.2 - Prob. 24WE Ch. 3.2 - Prob. 25WE Ch. 3.2 - Prob. 1MRE Ch. 3.2 - Prob. 2MRE Ch. 3.2 - Prob. 3MRE Ch. 3.2 - Prob. 4MRE Ch. 3.3 - Prob. 1CE Ch. 3.3 - Prob. 2CE Ch. 3.3 - Prob. 3CE Ch. 3.3 - Prob. 4CE Ch. 3.3 - Prob. 5CE Ch. 3.3 - Prob. 6CE Ch. 3.3 - Prob. 7CE Ch. 3.3 - Prob. 8CE Ch. 3.3 - Prob. 9CE Ch. 3.3 - Prob. 10CE Ch. 3.3 - Prob. 11CE Ch. 3.3 - Prob. 12CE Ch. 3.3 - Prob. 13CE Ch. 3.3 - Prob. 14CE Ch. 3.3 - Prob. 15CE Ch. 3.3 - Prob. 16CE Ch. 3.3 - Prob. 17CE Ch. 3.3 - Prob. 18CE Ch. 3.3 - Prob. 19CE Ch. 3.3 - Prob. 20CE Ch. 3.3 - Prob. 1WE Ch. 3.3 - Prob. 2WE Ch. 3.3 - Prob. 3WE Ch. 3.3 - Prob. 4WE Ch. 3.3 - Prob. 5WE Ch. 3.3 - Prob. 6WE Ch. 3.3 - Prob. 7WE Ch. 3.3 - Prob. 8WE Ch. 3.3 - Prob. 9WE Ch. 3.3 - Prob. 10WE Ch. 3.3 - Prob. 11WE Ch. 3.3 - Prob. 12WE Ch. 3.3 - Prob. 13WE Ch. 3.3 - Prob. 14WE Ch. 3.3 - Prob. 15WE Ch. 3.3 - Prob. 16WE Ch. 3.3 - Prob. 17WE Ch. 3.3 - Prob. 18WE Ch. 3.3 - Prob. 19WE Ch. 3.3 - Prob. 20WE Ch. 3.3 - Prob. 21WE Ch. 3.3 - Prob. 22WE Ch. 3.3 - Prob. 23WE Ch. 3.3 - Prob. 24WE Ch. 3.3 - Prob. 25WE Ch. 3.3 - Prob. 26WE Ch. 3.3 - Prob. 27WE Ch. 3.3 - Prob. 28WE Ch. 3.3 - Prob. 29WE Ch. 3.3 - Prob. 30WE Ch. 3.3 - Prob. 31WE Ch. 3.3 - Prob. 1ST1 Ch. 3.3 - Prob. 2ST1 Ch. 3.3 - Prob. 3ST1 Ch. 3.3 - Prob. 4ST1 Ch. 3.3 - Prob. 5ST1 Ch. 3.3 - Prob. 6ST1 Ch. 3.3 - Prob. 7ST1 Ch. 3.3 - Prob. 8ST1 Ch. 3.3 - Prob. 9ST1 Ch. 3.3 - Prob. 10ST1 Ch. 3.3 - Prob. 11ST1 Ch. 3.3 - Prob. 12ST1 Ch. 3.3 - Prob. 13ST1 Ch. 3.3 - Prob. 14ST1 Ch. 3.3 - Prob. 15ST1 Ch. 3.3 - Prob. 16ST1 Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.4 - Prob. 1CE Ch. 3.4 - Prob. 2CE Ch. 3.4 - Prob. 3CE Ch. 3.4 - Prob. 4CE Ch. 3.4 - Prob. 5CE Ch. 3.4 - Prob. 6CE Ch. 3.4 - Prob. 7CE Ch. 3.4 - Prob. 8CE Ch. 3.4 - Prob. 9CE Ch. 3.4 - Prob. 10CE Ch. 3.4 - Prob. 11CE Ch. 3.4 - Prob. 12CE Ch. 3.4 - Prob. 13CE Ch. 3.4 - Prob. 14CE Ch. 3.4 - Prob. 15CE Ch. 3.4 - Prob. 16CE Ch. 3.4 - Prob. 17CE Ch. 3.4 - Prob. 1WE Ch. 3.4 - Prob. 2WE Ch. 3.4 - Prob. 3WE Ch. 3.4 - Prob. 4WE Ch. 3.4 - Prob. 5WE Ch. 3.4 - Prob. 6WE Ch. 3.4 - Prob. 7WE Ch. 3.4 - Prob. 8WE Ch. 3.4 - Prob. 9WE Ch. 3.4 - Prob. 10WE Ch. 3.4 - Prob. 11WE Ch. 3.4 - Prob. 12WE Ch. 3.4 - Prob. 13WE Ch. 3.4 - Prob. 14WE Ch. 3.4 - Prob. 15WE Ch. 3.4 - Prob. 16WE Ch. 3.4 - Prob. 17WE Ch. 3.4 - Prob. 18WE Ch. 3.4 - Prob. 19WE Ch. 3.4 - Prob. 20WE Ch. 3.4 - Prob. 21WE Ch. 3.4 - Prob. 22WE Ch. 3.4 - Prob. 23WE Ch. 3.4 - Prob. 24WE Ch. 3.4 - Prob. 25WE Ch. 3.4 - Prob. 26WE Ch. 3.4 - Prob. 27WE Ch. 3.4 - Prob. 28WE Ch. 3.4 - Prob. 29WE Ch. 3.4 - Prob. 30WE Ch. 3.4 - Prob. 31WE Ch. 3.4 - Prob. 32WE Ch. 3.4 - Prob. 33WE Ch. 3.4 - Prob. 34WE Ch. 3.5 - Prob. 1CE Ch. 3.5 - Prob. 2CE Ch. 3.5 - Prob. 3CE Ch. 3.5 - Prob. 4CE Ch. 3.5 - Prob. 5CE Ch. 3.5 - Prob. 6CE Ch. 3.5 - Prob. 7CE Ch. 3.5 - Prob. 8CE Ch. 3.5 - Prob. 9CE Ch. 3.5 - Prob. 1WE Ch. 3.5 - Prob. 2WE Ch. 3.5 - Prob. 3WE Ch. 3.5 - Prob. 4WE Ch. 3.5 - Prob. 5WE Ch. 3.5 - Prob. 6WE Ch. 3.5 - Prob. 7WE Ch. 3.5 - Prob. 8WE Ch. 3.5 - Prob. 9WE Ch. 3.5 - Prob. 10WE Ch. 3.5 - Prob. 11WE Ch. 3.5 - Prob. 12WE Ch. 3.5 - Prob. 13WE Ch. 3.5 - Prob. 14WE Ch. 3.5 - Prob. 15WE Ch. 3.5 - Prob. 16WE Ch. 3.5 - Prob. 17WE Ch. 3.5 - Prob. 18WE Ch. 3.5 - Prob. 19WE Ch. 3.5 - Prob. 20WE Ch. 3.5 - Prob. 21WE Ch. 3.5 - Prob. 22WE Ch. 3.5 - Prob. 23WE Ch. 3.5 - Prob. 24WE Ch. 3.5 - Prob. 25WE Ch. 3.5 - Prob. 26WE Ch. 3.5 - Prob. 27WE Ch. 3.5 - Prob. 28WE Ch. 3.6 - Prob. 1CE Ch. 3.6 - Prob. 2CE Ch. 3.6 - Prob. 3CE Ch. 3.6 - Prob. 4CE Ch. 3.6 - Prob. 5CE Ch. 3.6 - Prob. 6CE Ch. 3.6 - Prob. 1WE Ch. 3.6 - Prob. 2WE Ch. 3.6 - Prob. 3WE Ch. 3.6 - Prob. 4WE Ch. 3.6 - Prob. 5WE Ch. 3.6 - Prob. 6WE Ch. 3.6 - Prob. 7WE Ch. 3.6 - Prob. 8WE Ch. 3.6 - Prob. 9WE Ch. 3.6 - Prob. 10WE Ch. 3.6 - Prob. 11WE Ch. 3.6 - Prob. 12WE Ch. 3.6 - Prob. 13WE Ch. 3.6 - Prob. 14WE Ch. 3.6 - Prob. 15WE Ch. 3.6 - Prob. 16WE Ch. 3.6 - Prob. 17WE Ch. 3.6 - Prob. 18WE Ch. 3.6 - Prob. 19WE Ch. 3.6 - Prob. 20WE Ch. 3.6 - Prob. 21WE Ch. 3.6 - Prob. 22WE Ch. 3.6 - Prob. 23WE Ch. 3.6 - Prob. 24WE Ch. 3.6 - Prob. 25WE Ch. 3.6 - Prob. 26WE Ch. 3.6 - Prob. 27WE Ch. 3.6 - Prob. 28WE Ch. 3.6 - Prob. 29WE Ch. 3.6 - Prob. 30WE Ch. 3.6 - Prob. 1ST2 Ch. 3.6 - Prob. 2ST2 Ch. 3.6 - Prob. 3ST2 Ch. 3.6 - Prob. 4ST2 Ch. 3.6 - Prob. 5ST2 Ch. 3.6 - Prob. 6ST2 Ch. 3.6 - Prob. 7ST2 Ch. 3.6 - Prob. 8ST2 Ch. 3.6 - Prob. 9ST2 Ch. 3.6 - Prob. 10ST2 Ch. 3.6 - Prob. 11ST2 Ch. 3.6 - Prob. 12ST2 Ch. 3.6 - Prob. 13ST2 Ch. 3.6 - Prob. 14ST2 Ch. 3.6 - Prob. 15ST2 Ch. 3 - Prob. 1CR Ch. 3 - Prob. 2CR Ch. 3 - Prob. 3CR Ch. 3 - Prob. 4CR Ch. 3 - Prob. 5CR Ch. 3 - Prob. 6CR Ch. 3 - Prob. 7CR Ch. 3 - Prob. 8CR Ch. 3 - Prob. 9CR Ch. 3 - Prob. 10CR Ch. 3 - Prob. 11CR Ch. 3 - Prob. 12CR Ch. 3 - Prob. 13CR Ch. 3 - Prob. 14CR Ch. 3 - Prob. 15CR Ch. 3 - Prob. 16CR Ch. 3 - Prob. 17CR Ch. 3 - Prob. 18CR Ch. 3 - Prob. 19CR Ch. 3 - Prob. 20CR Ch. 3 - Prob. 21CR Ch. 3 - Prob. 1CT Ch. 3 - Prob. 2CT Ch. 3 - Prob. 3CT Ch. 3 - Prob. 4CT Ch. 3 - Prob. 5CT Ch. 3 - Prob. 6CT Ch. 3 - Prob. 7CT Ch. 3 - Prob. 8CT Ch. 3 - Prob. 9CT Ch. 3 - Prob. 10CT Ch. 3 - Prob. 11CT Ch. 3 - Prob. 12CT Ch. 3 - Prob. 13CT Ch. 3 - Prob. 14CT Ch. 3 - Prob. 1AR Ch. 3 - Prob. 2AR Ch. 3 - Prob. 3AR Ch. 3 - Prob. 4AR Ch. 3 - Prob. 5AR Ch. 3 - Prob. 6AR Ch. 3 - Prob. 7AR Ch. 3 - Prob. 8AR Ch. 3 - Prob. 9AR Ch. 3 - Prob. 10AR Ch. 3 - Prob. 11AR Ch. 3 - Prob. 12AR Ch. 3 - Prob. 13AR Ch. 3 - Prob. 14AR Ch. 3 - Prob. 15AR Ch. 3 - Prob. 16AR Ch. 3 - Prob. 17AR Ch. 3 - Prob. 18AR Ch. 3 - Prob. 19AR Ch. 3 - Prob. 20AR Ch. 3 - Prob. 21AR Ch. 3 - Prob. 22AR Ch. 3 - Prob. 23AR Ch. 3 - Prob. 24AR Ch. 3 - Prob. 25AR Ch. 3 - Prob. 26AR Ch. 3 - Prob. 27AR Ch. 3 - Prob. 28AR Ch. 3 - Prob. 29AR Ch. 3 - Prob. 30AR Ch. 3 - Prob. 31AR Ch. 3 - Prob. 32AR Ch. 3 - Prob. 33AR Ch. 3 - Prob. 34AR Ch. 3 - Prob. 35AR Ch. 3 - Prob. 36AR Ch. 3 - Prob. 37AR Ch. 3 - Prob. 38AR Ch. 3 - Prob. 39AR Ch. 3 - Prob. 40AR Ch. 3 - Prob. 1CUR Ch. 3 - Prob. 2CUR Ch. 3 - Prob. 3CUR Ch. 3 - Prob. 4CUR Ch. 3 - Prob. 5CUR Ch. 3 - Prob. 6CUR Ch. 3 - Prob. 7CUR Ch. 3 - Prob. 8CUR Ch. 3 - Prob. 9CUR Ch. 3 - Prob. 10CUR Ch. 3 - Prob. 11CUR Ch. 3 - Prob. 12CUR Ch. 3 - Prob. 13CUR Ch. 3 - Prob. 14CUR Ch. 3 - Prob. 15CUR Ch. 3 - Prob. 16CUR Ch. 3 - Prob. 17CUR Ch. 3 - Prob. 18CUR Ch. 3 - Prob. 19CUR Ch. 3 - Prob. 20CUR Ch. 3 - Prob. 21CUR Ch. 3 - Prob. 22CUR Ch. 3 - Prob. 23CUR Ch. 3 - Prob. 24CUR Ch. 3 - Prob. 25CUR Ch. 3 - Prob. 26CUR Ch. 3 - Prob. 27CUR Ch. 3 - Prob. 28CUR Ch. 3 - Prob. 29CUR Ch. 3 - Prob. 30CUR Ch. 3 - Prob. 31CUR Ch. 3 - Prob. 32CUR Ch. 3 - Prob. 33CUR Ch. 3 - Prob. 34CUR Ch. 3 - Prob. 35CUR Ch. 3 - Prob. 36CUR Ch. 3 - Prob. 37CUR Ch. 3 - Prob. 38CUR Ch. 3 - Prob. 39CUR Ch. 3 - Prob. 40CUR Ch. 3 - Prob. 41CUR Ch. 3 - Prob. 42CUR Ch. 3 - Prob. 43CUR Ch. 3 - Prob. 44CUR Ch. 3 - Prob. 45CUR Ch. 3 - Prob. 46CUR

Additional Math Textbook Solutions

Find more solutions based on key concepts

Using the Empirical Rule In Exercises 29–34, use the Empirical Rule. 34. The monthly utility bills for eight ho...

Elementary Statistics: Picturing the World (7th Edition)

In Problems 19-26, sketch the graph of each function. Be sure to label three points on the graph. f( x )= 1 x

Precalculus

In Exercises 5–8, r(t) is the position of a particle in the xy-plane at time t. Find an equation in x and y who...

University Calculus: Early Transcendentals (4th Edition)

In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...

Elementary Statistics (13th Edition)

The function y=−2x3

Pre-Algebra Student Edition

1. combination of numbers, variables, and operation symbols is called an algebraic______.

Algebra and Trigonometry (6th Edition)

Knowledge Booster

$Geometry$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.