
Concept explainers
a)
To find: Three pairs of same side interior
a)
Answer to Problem 21WE
When lines l and n are intersected by a transversal, then form
Explanation of Solution
Given information: In below figure, lines l and n are intersected by a transversal, so that on its interior same side, two angles
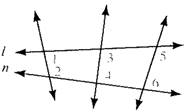
Concept used: By property of parallel lines, if two parallel lines are cut by a transversal, then the sum of two angles formed on the same side of the transversal between these parallel lines is 180 degree.
Explanation: As it form
b)
To find: Three pairs of same side interior angles on the same sides of transversals in the given figure and also to find the sum of two angles of pair
b)
Answer to Problem 21WE
When lines l and n are intersected by a transversal, then form
Explanation of Solution
Given information: In below figure, lines l and n are intersected by a transversal, so that on its interior same side, two angles
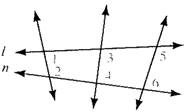
Concept used: By property of parallel lines, if two parallel lines are cut by a transversal, then the sum of two angles formed on the same side of the transversal between these parallel lines is 180 degree.
Explanation: As it form
c)
To find: Three pairs of same side interior angles on the same sides of transversals in the given figure and also to find the sum of two angles of each pair.
c)
Answer to Problem 21WE
When lines l and n are intersected by a transversal, then form
Explanation of Solution
Given information: In below figure, lines l and n are intersected by a transversal, so that on its interior same side, two angles
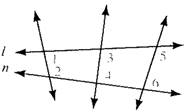
Concept used: By property of parallel lines, if two parallel lines are cut by a transversal, then the sum of two angles formed on the same side of the transversal between these parallel lines is 180 degree.
As it form
d)
To find: The information from the given figure that shows that two lines l and n are intersected by a transversal, so that two angles on the same interior angles form there.
d)
Answer to Problem 21WE
When lines l and n are intersected by one or more transversals, the sum of two interior angles on the same side of any of the transversal, always remains equal to 180 degree.
Explanation of Solution
Given information: In below figure, lines l and n are intersected by one or more transversals, so that on its interior same side, different pairs of two angles form.
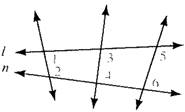
Concept used: By property of parallel lines, if two parallel lines are cut by a transversal, then the sum of two angles formed on the same side of the transversal between these parallel lines is 180 degree.
So, it is concluded that when one or more transversals cut two parallel lines l and n, the sum of two interior angles, forming on the same side of any of the transversal is always equal to 180 degree.
Chapter 3 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics
Basic Business Statistics, Student Value Edition
- 6arrow_forwardDoor 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

