Precalculus with Limits
3rd Edition
ISBN: 9781133947202
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 3.5, Problem 65E
To determine
To write John Napier’s work with logarithms.
Expert Solution & Answer
Explanation of Solution
In 1614, the method of logarithms was propounded by John Napier publicly in a book which was entitled as “Mirifici Logarithmorum Canonis Descriptio”. The meaning of this book was also called as (Description of the Wonderful Rule of Logarithms).
By the use of repeated subtractions Napier calculated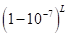 
for L ranging from 1 to 100. The result for 
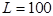is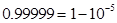 
Napier calculated the products of the numbers then with 
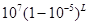for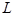 
from 1 to 50, and did similarly with 
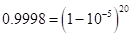and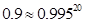 
. Finally, from these computations, Napier allowed to give him for any number N from 5 to 10 million, the number L that solves the equation
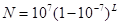
First Napier called L and artificial number but the word “logarithm” has been introduced later here : “logos” meaning proportion, and “arithmos” meaning number. In modern notation, the relation to natural logarithms is:
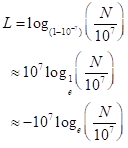
where the very close approximation corresponds to the observation that
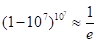
Chapter 3 Solutions
Precalculus with Limits
Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Prob. 75ECh. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - Prob. 80ECh. 3.1 - Prob. 81ECh. 3.1 - Prob. 82ECh. 3.1 - Prob. 83ECh. 3.1 - Prob. 84ECh. 3.1 - Prob. 85ECh. 3.1 - Prob. 86ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - Prob. 77ECh. 3.2 - Prob. 78ECh. 3.2 - Prob. 79ECh. 3.2 - Prob. 80ECh. 3.2 - Prob. 81ECh. 3.2 - Prob. 82ECh. 3.2 - Prob. 83ECh. 3.2 - Prob. 84ECh. 3.2 - Prob. 85ECh. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.2 - Prob. 89ECh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.3 - Prob. 71ECh. 3.3 - Prob. 72ECh. 3.3 - Prob. 73ECh. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - Prob. 77ECh. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Prob. 81ECh. 3.3 - Prob. 82ECh. 3.3 - Prob. 83ECh. 3.3 - Prob. 84ECh. 3.3 - Prob. 85ECh. 3.3 - Prob. 86ECh. 3.3 - Prob. 87ECh. 3.3 - Prob. 88ECh. 3.3 - Prob. 89ECh. 3.3 - Prob. 90ECh. 3.3 - Prob. 91ECh. 3.3 - Prob. 92ECh. 3.3 - Prob. 93ECh. 3.3 - Prob. 94ECh. 3.3 - Prob. 95ECh. 3.3 - Prob. 96ECh. 3.3 - Prob. 97ECh. 3.3 - Prob. 98ECh. 3.3 - Prob. 99ECh. 3.3 - Prob. 100ECh. 3.3 - Prob. 101ECh. 3.3 - Prob. 102ECh. 3.3 - Prob. 103ECh. 3.3 - Prob. 104ECh. 3.3 - Prob. 105ECh. 3.3 - Prob. 106ECh. 3.3 - Prob. 107ECh. 3.3 - Prob. 108ECh. 3.3 - Prob. 109ECh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Prob. 80ECh. 3.4 - Prob. 81ECh. 3.4 - Prob. 82ECh. 3.4 - Prob. 83ECh. 3.4 - Prob. 84ECh. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - Prob. 99RECh. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - Prob. 102RECh. 3 - Prob. 103RECh. 3 - Prob. 104RECh. 3 - Prob. 105RECh. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Prob. 110RECh. 3 - Prob. 111RECh. 3 - Prob. 112RECh. 3 - Prob. 113RECh. 3 - Prob. 114RECh. 3 - Prob. 115RECh. 3 - Prob. 116RECh. 3 - Prob. 117RECh. 3 - Prob. 118RECh. 3 - Prob. 119RECh. 3 - Prob. 120RECh. 3 - Prob. 1CTCh. 3 - Prob. 2CTCh. 3 - Prob. 3CTCh. 3 - Prob. 4CTCh. 3 - Prob. 5CTCh. 3 - Prob. 6CTCh. 3 - Prob. 7CTCh. 3 - Prob. 8CTCh. 3 - Prob. 9CTCh. 3 - Prob. 10CTCh. 3 - Prob. 11CTCh. 3 - Prob. 12CTCh. 3 - Prob. 13CTCh. 3 - Prob. 14CTCh. 3 - Prob. 15CTCh. 3 - Prob. 16CTCh. 3 - Prob. 17CTCh. 3 - Prob. 18CTCh. 3 - Prob. 19CTCh. 3 - Prob. 20CTCh. 3 - Prob. 21CTCh. 3 - Prob. 22CTCh. 3 - Prob. 23CTCh. 3 - Prob. 24CTCh. 3 - Prob. 25CTCh. 3 - Prob. 26CTCh. 3 - Prob. 27CTCh. 3 - Prob. 28CTCh. 3 - Prob. 29CTCh. 3 - Prob. 1CLTCh. 3 - Prob. 2CLTCh. 3 - Prob. 3CLTCh. 3 - Prob. 4CLTCh. 3 - Prob. 5CLTCh. 3 - Prob. 6CLTCh. 3 - Prob. 7CLTCh. 3 - Prob. 8CLTCh. 3 - Prob. 9CLTCh. 3 - Prob. 10CLTCh. 3 - Prob. 11CLTCh. 3 - Prob. 12CLTCh. 3 - Prob. 13CLTCh. 3 - Prob. 14CLTCh. 3 - Prob. 15CLTCh. 3 - Prob. 16CLTCh. 3 - Prob. 17CLTCh. 3 - Prob. 18CLTCh. 3 - Prob. 19CLTCh. 3 - Prob. 20CLTCh. 3 - Prob. 21CLTCh. 3 - Prob. 22CLTCh. 3 - Prob. 23CLTCh. 3 - Prob. 24CLTCh. 3 - Prob. 25CLTCh. 3 - Prob. 26CLTCh. 3 - Prob. 27CLTCh. 3 - Prob. 28CLTCh. 3 - Prob. 29CLTCh. 3 - Prob. 30CLTCh. 3 - Prob. 31CLTCh. 3 - Prob. 32CLTCh. 3 - Prob. 33CLTCh. 3 - Prob. 34CLTCh. 3 - Prob. 35CLTCh. 3 - Prob. 36CLTCh. 3 - Prob. 37CLTCh. 3 - Prob. 38CLTCh. 3 - Prob. 39CLTCh. 3 - Prob. 40CLTCh. 3 - Prob. 41CLTCh. 3 - Prob. 42CLTCh. 3 - Prob. 1PSCh. 3 - Prob. 2PSCh. 3 - Prob. 3PSCh. 3 - Prob. 4PSCh. 3 - Prob. 5PSCh. 3 - Prob. 6PSCh. 3 - Prob. 7PSCh. 3 - Prob. 8PSCh. 3 - Prob. 9PSCh. 3 - Prob. 10PSCh. 3 - Prob. 11PSCh. 3 - Prob. 12PSCh. 3 - Prob. 13PSCh. 3 - Prob. 14PSCh. 3 - Prob. 15PSCh. 3 - Prob. 16PSCh. 3 - Prob. 17PSCh. 3 - Prob. 18PSCh. 3 - Prob. 19PSCh. 3 - Prob. 20PSCh. 3 - Prob. 21PSCh. 3 - Prob. 22PSCh. 3 - Prob. 23PSCh. 3 - Prob. 24PSCh. 3 - Prob. 25PSCh. 3 - Prob. 26PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Solve the differential equation. 37 6 dy = 2x³y7 - 4x³ dxarrow_forwardFind an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 3xy.arrow_forwardQ6. A fossil piece has been found in Alberta that contains 34% of C14 in it. What is the age of this fossil piece?arrow_forward
- Q5. Briefly explain what are isotopes of an elements, with an example, and why some isotopes are radioactive. 470arrow_forwardQ1. Will you earn more interest amount in two years by depositing $2000 in a simple interest account that pays 6% or in an account that pays 6.15% interest compounded monthly? tarrow_forwardQ4. We want to invest $18000 in an account compounded continuously. How long should the investment be kept so final value of the account reaches $25000 if the annual rate of interest is 5.8%?arrow_forward
- Q3. Determine the effective annual yield for each investment below. Then select the better investment. Assume 365 days in a year. a) 5.6% compounded semiannually; b) 5.4% compounded daily.arrow_forwardQ2. You deposit $22,000 in an account that pays 4.8% interest compounded monthly. a. Find the future value after six years. & b b. Determine the effective annual yield of this account.arrow_forward18. Using the method of variation of parameter, a particular solution to y′′ + 16y = 4 sec(4t) isyp(t) = u1(t) cos(4t) + u2(t) sin(4t). Then u2(t) is equal toA. 1 B. t C. ln | sin 4t| D. ln | cos 4t| E. sec(4t)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Implicit Differentiation with Transcendental Functions; Author: Mathispower4u;https://www.youtube.com/watch?v=16WoO59R88w;License: Standard YouTube License, CC-BY
How to determine the difference between an algebraic and transcendental expression; Author: Study Force;https://www.youtube.com/watch?v=xRht10w7ZOE;License: Standard YouTube License, CC-BY