Chapter 3.2, Problem 42E

To determine

To find the domain, $x$ - intercepts, vertical asymptotes and to sketch the graph of the function

  $g(x)={\log }_{6}x$ .

Answer to Problem 42E

  $\left(0,\infty \right)$

Explanation of Solution

Given:

Function: $g(x)={\log }_{6}x$

Formula used:

  ${\log }_{a}b=c\iff b=a^c$

Calculation:

Finding the domain of the function,

When $x>0$ , the function is defined.

So, the domain of the function is $\left(0,\infty \right).$

To find the x-intercept, put $g(x)=y=0$ in given function.

  $\begin{array}{c}\Rightarrow 0={\log }_{6}x\\ \Rightarrow x=6^0[\because {\log }_{a}b=c\iff b=a^c]\\ \Rightarrow x=1\end{array}$

So, x-intercept is $\left(1,0\right)$ .

Asymptotes:

Vertical asymptotes:

To find vertical asymptotes, put the value of the given function in logarithmic part equal to zero.

  $\Rightarrow x=0$

So, the vertical asymptote is $x=0.$

Calculation for graph:

Consider $g(x)={\log }_{6}x$

Values of x	Values of g(x)
1	0
2	0.387
3	0.613

By taking different values of x, the graph can be plotted.

Graph:

  

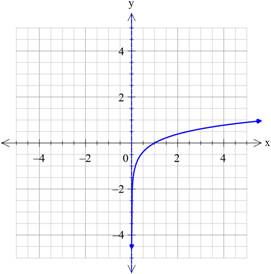
Interpretation:

The above graph represents the sketch of given function.