Chapter 3.4, Problem 7SP

How fast can a racecar travel through a circular tum without skidding and hitting the wall? The answer could depend on several factors:

• The weight of the car;
• The friction between the tires and the road;
• The radius of the circle;
• The “steepness” of the turn.

In this project we investigate this question for NASCAR racecars at the Bristol Motor Speedway in Tennessee. Before considering this track in particular, we use vector functions to develop the mathematics and physics necessary for answering questions such as this.

A car of mass m moves with constant angular speed to around a circular curve of radius R (Figure 3.20). The curve is banked at an angle $\theta$ . If the height of the car off the ground is h, then the position of the car at time t is given by the function $r\left(t\right)\langle R\cos \left(\omega t\right),R\sin \left(\omega t\right),h\rangle$ .

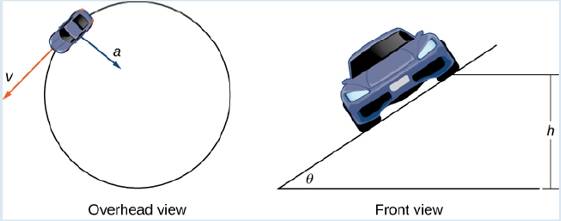
Figure 3.20 Views of a lace ear moving around a track.

As the car moves around the curve, three forces act on it: gravity, the force exerted by the road (this force is perpendicular to the ground), and the friction force (Figure 3.21). Because describing the frictional force generated by the tires and the road is complex, we use a standard approximation for the frictional force. Assume that $\text{f}=\mu N$ for some positive constant $\mu$ . The constant $\mu$ is called the coefficient of friction.

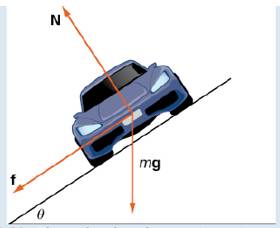
Figure 3.21 The car has three forces acting on it: gravity (denoted by mg), the friction force f, and the force exerted by the road N.

Let $v_{\max }$ denote the maximum speed the car can attain through the curve without skidding. In other words, $v_{\max }$ is the fastest speed at which the car can navigate the turn. When the car is navigate at this speed, the magnitude of the centripetal force is

   $\left|F_{cent}\right|=\frac{m{v}_{\max }^2}{R}$

The next three questions deal with developing a formula that relates the speed $v_{\max }$ to the banking angle $\theta$ .

7. Show that $v_{\max }^2=\left(\left(\sin \theta +\mu \cos \theta \right)/\left(\cos \theta -\mu \sin \theta \right)\right)gR$ . Conclude that the maximum speed does not actually depend on the mass of the car.

Now that we have a formula relating the maximum speed of the car and the banking angle, we are in a position to answer the questions like the one posed at the beginning of the project.

The Bristol Motor Speedway is a NASCAR short track in Bristol, Tennessee. The track has the approximate shape shown in Figure 3.22. Each end of the track is approximately semicircular, so when cars make turns they are traveling along an approximately circular curve. If a car takes the inside track and speeds along the bottom of turn 1, the car travels along a semicircle of radius approximately $\text{211 ft}$ with a banking angle of $\text{24}°$ . If the car decides to take the outside track and speeds along the top of turn 1, then the car travels along a semicircle with a banking angle of 28°. (The track has variable angle banking.)

Figure 3.22 At the Bristol Motor Speedway, Bristol, Tennessee (a), the turns have an inner radius of about $\text{211 ft}$ and a width of $\text{4}0\text{ ft}$ (b). (credit: part (c) photo by Raniel Diaz, Flickr)

The coefficient of friction for a normal fire in Elly conditions is approximately $0.\text{7}$ . Therefore, we assume the coefficient for a NASCAR tire in dry conditions is approximately $0.\text{93}$ .