Chapter 3.4, Problem 6SP

How fast can a racecar travel through a circular tum without skidding and hitting the wall? The answer could depend on several factors:

• The weight of the car;
• The friction between the tires and the road;
• The radius of the circle;
• The “steepness” of the turn.

In this project we investigate this question for NASCAR racecars at the Bristol Motor Speedway in Tennessee. Before considering this track in particular, we use vector functions to develop the mathematics and physics necessary for answering questions such as this.

A car of mass m moves with constant angular speed to around a circular curve of radius R (Figure 3.20). The curve is banked at an angle $\theta$ . If the height of the car off the ground is h, then the position of the car at time t is given by the function $r\left(t\right)\langle R\cos \left(\omega t\right),R\sin \left(\omega t\right),h\rangle$ .

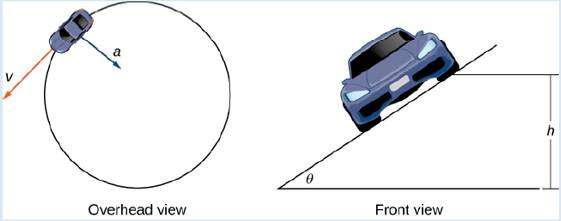
Figure 3.20 Views of a lace ear moving around a track.

As the car moves around the curve, three forces act on it: gravity, the force exerted by the road (this force is perpendicular to the ground), and the friction force (Figure 3.21). Because describing the frictional force generated by the tires and the road is complex, we use a standard approximation for the frictional force. Assume that $\text{f}=\mu N$ for some positive constant $\mu$ . The constant $\mu$ is called the coefficient of friction.

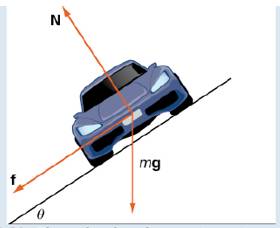
Figure 3.21 The car has three forces acting on it: gravity (denoted by mg), the friction force f, and the force exerted by the road N.

Let $v_{\max }$ denote the maximum speed the car can attain through the curve without skidding. In other words, $v_{\max }$ is the fastest speed at which the car can navigate the turn. When the car is navigate at this speed, the magnitude of the centripetal force is

     $\left|F_{cent}\right|=\frac{m{v}_{\max }^2}{R}$

The next three questions deal with developing a formula that relates the speed $v_{\max }$ to the banking angle $\theta$ .

6. The centripetal force is the sum of the forces in the horizontal direction, since the centripetal force points toward the center of the circular curve. Show that

${\text{f}}_{cent}=N\sin \theta +\text{f}\cos \theta$ .

Conclude that     ${\text{f}}_{cent}=\frac{\sin \theta +\mu \cos \theta }{\cos \theta -\mu \sin \theta }mg.$