Engineering Mechanics: Statics & Dynamics (14th Edition)
14th Edition
ISBN: 9780133915426
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.4, Problem 46P
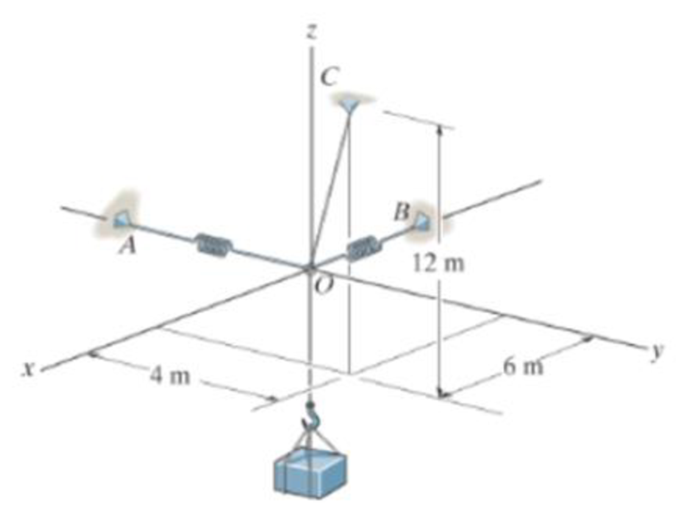
Determine the stretch in each of die two springs required to hold the 20-kg crate in the equilibrium position shown. Each spring has on unstretched length of 2 m and a stiffness of k = 300 N/m.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Each spring has an unstretched length of 2 in and a stiffness of fc = 330 N/m .
1. Determine the stretch in 04 spring required to hold the 18-kg crate in the equilibrium position shown.
2. Determine the stretch in OB spring required to hold the 18-kg crate in the equilibrium position shown.
Each spring has an unstretched length of 2 mm and a stiffness of k = 350 N/m.
Determine the stretch in OA spring required to hold the 25-kg crate in the equilibrium position shown.
Determine the stretch in OB spring required to hold the 25-kg crate in the equilibrium position shown.
Determine the stretch in each spring for for equilibrium of the 1.8-kg
block. The springs are shown in the equilibrium position. (Figure 1)
No elements selected
3m
4 m
3 m
kAC = 20 N/m
igure
kan = 30 N/m
www
1 of 1
3 m
4 m
kAD- 40 N/m
3 m
kAc = 20 N/m
kAn- 30 N/m
www
kAD- 40 N/m
Select the elements from the list and add them to the canvas setting the appropriate attributes.
Chapter 3 Solutions
Engineering Mechanics: Statics & Dynamics (14th Edition)
Ch. 3.3 - In each case, draw a free-body diagram of the ring...Ch. 3.3 - Write the two equations of equilibrium, Fx = 0 and...Ch. 3.3 - The crate has a weight of 550 lb. Determine the...Ch. 3.3 - The beam has a weight of 700 lb. Determine the...Ch. 3.3 - If the 5-kg block is suspended from the pulley B...Ch. 3.3 - The block has a mass of 5 kg and rests on the...Ch. 3.3 - If the mass of cylinder C is 40 kg, determine the...Ch. 3.3 - Determine the tension in cables AB, BC, and CD,...Ch. 3.3 - The members of a truss are pin connected at joint...Ch. 3.3 - The members of a truss are pin connected at joint...
Ch. 3.3 - Determine the magnitude and direction of F so...Ch. 3.3 - The bearing consists of rollers, symmetrically...Ch. 3.3 - The members of a truss are connected to the gusset...Ch. 3.3 - The gusset plate is subjected to the forces of...Ch. 3.3 - The man attempts to pull down the tree using the...Ch. 3.3 - The cords ABC and BD can each support a maximum...Ch. 3.3 - Determine the maximum force F that can be...Ch. 3.3 - The block has a weight of 20 lb and is being...Ch. 3.3 - Determine the maximum weight W of the block that...Ch. 3.3 - The lift sling is used to hoist a container having...Ch. 3.3 - A nuclear-reactor vessel has a weight of 500(103)...Ch. 3.3 - Determine the stretch in each spring for...Ch. 3.3 - The unstretched length of spring AB is 3 m. If the...Ch. 3.3 - Determine the mass of each of the two cylinders if...Ch. 3.3 - Determine the stiffness kT of the single spring...Ch. 3.3 - If the spring DB has an unstretched length of 2 m....Ch. 3.3 - Determine the unstretched length of DB to hold the...Ch. 3.3 - A vertical force P = 10 lb is applied to the ends...Ch. 3.3 - Determine the unstretched length of spring AC if a...Ch. 3.3 - The springs BA and BC each have a stiffness of 500...Ch. 3.3 - The springs BA and BC each nave a stiffness of 500...Ch. 3.3 - Determine the distances x and y for equilibrium if...Ch. 3.3 - Determine the magnitude of F1 and the distance y...Ch. 3.3 - The 30-kg pipe is supported at A by a system of...Ch. 3.3 - Each cord can sustain a maximum tension of 500 N....Ch. 3.3 - The streetlights A and B are suspended from the...Ch. 3.3 - Determine the tension developed in each cord...Ch. 3.3 - Prob. 30PCh. 3.3 - Prob. 31PCh. 3.3 - Prob. 32PCh. 3.3 - The lamp has a weight of 15 lb and is supported by...Ch. 3.3 - Each cord can sustain a maximum tension of 20 lb....Ch. 3.3 - Prob. 35PCh. 3.3 - Prob. 36PCh. 3.3 - Prob. 37PCh. 3.3 - Prob. 38PCh. 3.3 - The ball D has a mass of 20 kg. If a force of F =...Ch. 3.3 - The 200-lb uniform container is suspended by means...Ch. 3.3 - The single elastic cord ABC is used to support the...Ch. 3.3 - A scale is constructed with a 4-ft-long cord and...Ch. 3.3 - The concrete wall panel is hoisted into position...Ch. 3.3 - Prob. 2CPCh. 3.3 - Prob. 3CPCh. 3.3 - Prob. 4CPCh. 3.4 - Determine the magnitude of forces F1, F2, F3, so...Ch. 3.4 - Determine the tension developed in cables AB, AC,...Ch. 3.4 - Prob. 9FPCh. 3.4 - Prob. 10FPCh. 3.4 - Prob. 11FPCh. 3.4 - The three cables are used to support the 40-kg...Ch. 3.4 - Determine the magnitudes of F1, F2, and F3 for...Ch. 3.4 - If the bucket and its contents have a total weight...Ch. 3.4 - Determine the stretch in each of die two springs...Ch. 3.4 - Prob. 47PCh. 3.4 - Determine the tension in the cables in order to...Ch. 3.4 - Determine the maximum mass of the crate so that...Ch. 3.4 - Determine the force in each cable if F = 500 lb.Ch. 3.4 - Prob. 51PCh. 3.4 - Determine the tens on developed in cables AB and...Ch. 3.4 - If the tension developed in each cable cannot...Ch. 3.4 - Prob. 54PCh. 3.4 - Determine the maximum weight of the crate that can...Ch. 3.4 - The 25 kg flowerpot is supported at A by the three...Ch. 3.4 - If each cord can sustain a maximum tension of 50 N...Ch. 3.4 - Determine the tension developed m the three cables...Ch. 3.4 - Determine the tension developed in the three...Ch. 3.4 - Prob. 60PCh. 3.4 - Prob. 61PCh. 3.4 - If the maximum force in each rod con not exceed...Ch. 3.4 - Prob. 63PCh. 3.4 - If cable AD is tightened by a turnbuckle and...Ch. 3.4 - Prob. 65PCh. 3.4 - Prob. 66PCh. 3.4 - Determine the maximum weight of the crate so that...Ch. 3.4 - The pipe is held in place by the vise. If the bolt...Ch. 3.4 - Prob. 2RPCh. 3.4 - Prob. 3RPCh. 3.4 - Prob. 4RPCh. 3.4 - Prob. 5RPCh. 3.4 - Prob. 6RPCh. 3.4 - Determine the force in each cable needed to...Ch. 3.4 - If cable AB is subjected to a tension of 700 N,...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The two uniform cylinders, each of weight W, are resting against inclined surfaces. Neglecting friction, draw the free-body diagrams for each cylinder and for the two cylinders together. Count the total number of unknowns and the total number of independent equilibrium equations.arrow_forwardThe weightless bars AB and CE, together with the 5-lb weight BE, form a parallelogram linkage. The ideal spring attached to D has a free length of 2 in. and a stiffness of 7.5 lb/in. Find the two equilibrium positions that are in the range 0/2, and determine their stability. Neglect the weight of slider F.arrow_forwardThe 14-kN weight is suspended from a small pulley that is free to roll on the cable. The length of the cable ABC is 20 m. Determine the horizontal force P that would hold the pulley in equilibrium in the position x=5m.arrow_forward
- The 40-kghomogeneous disk is placed on a frictionless inclined surface and held in equilibrium by the horizontal force P and a couple C (C is not shown on the figure). Find P and C.arrow_forwardEquilibrium of a Particle 3-46. Determine the stretch in each of the two springs required to hold the 20-kg crate in the equilibrium position shown. Each spring has an unstretched length of 2 m and a stiffness of k 300 N/m. F=K.S (0,,k 12 m 4m 6 m Prob. 3-46 +2arrow_forward1. Determine the stretch in each of the two springs required to hold the 20-kg crate in the equilibrium position shown. Each spring has an unstretched length of 2 m and a stiffness of k = 300 N/m. 4m 12 m 6 marrow_forward
- Determine the ratio P/Q of the forces that are required to maintain equilibrium of the mechanism for an arbitrary angle 0. Neglect the weight of the mechanism.arrow_forwardA.The bar of negligible weight is supported by two springs, each having a stiffness k = 98 N/m. If the springs are originally unstretched, and the force is vertical as shown, determine the angle the bar makes with the horizontal, when the 31-N force is applied to the bar. B.Determine the stiffness k of each spring so that the 32-N force causes the bar to tip = 13.6° when the force is applied. Originally the bar is horizontal and the springs are unstretched. Neglect the weight of the bar.arrow_forward45 lb 4=0.40 4 = 0.30 Determine whether the block shown is in equilibrium and find the magnitude and direction of the friction force when P= 100 lb. 40arrow_forward
- When the 0.05-kg body is in the position shown, the linear spring is stretched 10 mm. Determine the force P required to break contact at C. Complete so lutions for (a) including the effects of the weight and (b) neglecting the weight.arrow_forwardThe 10 Ib weight is supported by the cord AC, a roller and by a spring. If the spring has an unstretched length of 8 in. and the weight is in equilibrium when d = 4 in., determine the stiffness k of the spring. 12 in. in A Select one: O a.k= 4.8 lb/in Ob.k=7.8 Ib/in Oc.k=6.8 Ib/in Od.k=5.8 Ib/inarrow_forward1. The cord AB has a length of 5 m and is attached to the end B of the spring having a stiffness k = 10 N/m. The other end of the spring is attached to a roller C so that the spring remains horizontal as it stretches. If a 10 N weight is suspended from B, determine the necessary un-stretched length of the spring, so that = 40° for equilibrium. 5 m 5 m 5 m- www k = 10 N/marrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Mechanical SPRING DESIGN Strategy and Restrictions in Under 15 Minutes!; Author: Less Boring Lectures;https://www.youtube.com/watch?v=dsWQrzfQt3s;License: Standard Youtube License