Bundle: College Algebra, Loose-leaf Version, 10th + WebAssign Printed Access Card for Larson's College Algebra, 10th Edition, Single-Term
10th Edition
ISBN: 9781337604857
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.3, Problem 82E
Lyme Disease
The numbers
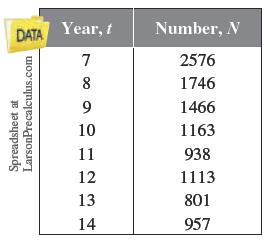
(a) Use a graphing utility to create a
(b) Use the regression feature of the graphing utility to find a quartic model for the data. (A quartic model has the form
(c) Use the model to create a table of estimated values of
(d) Use synthetic division to confirm algebraically your estimated value for the year 2014.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Compare the interest earned from #1 (where simple interest was used) to #5 (where compound interest was used). The principal, annual interest rate, and time were all the same; the only difference was that for #5, interest was compounded quarterly. Does the difference in interest earned make sense? Select one of the following statements. a. No, because more money should have been earned through simple interest than compound interest. b. Yes, because more money was earned through simple interest. For simple interest you earn interest on interest, not just on the amount of principal. c. No, because more money was earned through simple interest. For simple interest you earn interest on interest, not just on the amount of principal. d. Yes, because more money was earned when compounded quarterly. For compound interest you earn interest on interest, not just on the amount of principal.
Compare and contrast the simple and compound interest formulas. Which one of the following statements is correct? a. Simple interest and compound interest formulas both yield principal plus interest, so you must subtract the principal to get the amount of interest. b. Simple interest formula yields principal plus interest, so you must subtract the principal to get the amount of interest; Compound interest formula yields only interest, which you must add to the principal to get the final amount. c. Simple interest formula yields only interest, which you must add to the principal to get the final amount; Compound interest formula yields principal plus interest, so you must subtract the principal to get the amount of interest. d. Simple interest and compound interest formulas both yield only interest, which you must add to the principal to get the final amount.
Sara would like to go on a vacation in 5 years and she expects her total costs to be $3000. If she invests $2500 into a savings account for those 5 years at 8% interest, compounding semi-annually, how much money will she have? Round your answer to the nearest cent. Show you work. Will she be able to go on vacation? Why or why not?
Chapter 3 Solutions
Bundle: College Algebra, Loose-leaf Version, 10th + WebAssign Printed Access Card for Larson's College Algebra, 10th Edition, Single-Term
Ch. 3.1 - Sketch the graph of each quadratic function and...Ch. 3.1 - Prob. 2ECPCh. 3.1 - Sketch the graph of f(x)=x24x+3. Identify the...Ch. 3.1 - Write the standard form of the quadratic function...Ch. 3.1 - Rework Example 5 when the path of the baseball is...Ch. 3.1 - Prob. 1ECh. 3.1 - Fill in the blanks. A polynomial function of x...Ch. 3.1 - Fill in the blanks. A function is a second-degree...Ch. 3.1 - Fill in the blanks. When the graph of a quadratic...Ch. 3.1 - In Exercises 5-8, match the quadratic function...
Ch. 3.1 - In Exercises 5-8, match the quadratic function...Ch. 3.1 - In Exercises 5-8, match the quadratic function...Ch. 3.1 - In Exercises 5-8, match the quadratic function...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - In Exercises 13-26, write the quadratic function...Ch. 3.1 - In Exercises 13-26, write the quadratic function...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 19ECh. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 24ECh. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 26ECh. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - In Exercises 35 and 36, write the standard form of...Ch. 3.1 - In Exercises 35 and 36, write the standard form of...Ch. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 40ECh. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 42ECh. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 44ECh. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 46ECh. 3.1 - In Exercises 47-50, determine the x-intercept(s)...Ch. 3.1 - Graphical Reasoning In Exercises 47-50, determine...Ch. 3.1 - Graphical Reasoning In Exercises 47-50, determine...Ch. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - In Exercises 63-66, find two positive real numbers...Ch. 3.1 - In Exercises 63-66, find two positive real numbers...Ch. 3.1 - Path of a Diver The path of a diver is modeled by...Ch. 3.1 - Height of a Ball The path of a punted football is...Ch. 3.1 - Minimum Cost A manufacturer of lighting fixtures...Ch. 3.1 - Maximum Profit The profit P (in hundreds of...Ch. 3.1 - Maximum Revenue The total revenue R earned (in...Ch. 3.1 - Maximum Revenue The total revenue R earned per day...Ch. 3.1 - Maximum Area A rancher has 200 feet of fencing to...Ch. 3.1 - Maximum Area A Norman window is constructed by...Ch. 3.1 - Prob. 75ECh. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - The graph shows a quadratic function of the form...Ch. 3.1 - Proof Assume that the function f(x)=ax2+bx+c,a0...Ch. 3.2 - Sketch the graph of each function....Ch. 3.2 - Describe the left-hand and right-hand behavior of...Ch. 3.2 - Prob. 3ECPCh. 3.2 - Prob. 4ECPCh. 3.2 - Prob. 5ECPCh. 3.2 - Prob. 6ECPCh. 3.2 - Fill in the blanks. The graph of a polynomial...Ch. 3.2 - Fill in the blanks. The is used to determine...Ch. 3.2 - Fill in the blanks. A polynomial function of...Ch. 3.2 - Fill in the blanks. When x=a is a zero of a...Ch. 3.2 - Fill in the blanks. When a real zero xa of a...Ch. 3.2 - Fill in the blanks. A factor xak,k1, yields a ...Ch. 3.2 - Fill in the blanks. A polynomial function is...Ch. 3.2 - Fill in the blanks. The Theorem states that if fis...Ch. 3.2 - In Exercises 9-14, match the polynomial function...Ch. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - In Exercises 9-14, match the polynomial function...Ch. 3.2 - In Exercises 9-14, match the polynomial function...Ch. 3.2 - Sketching Transformations of Monomial Functions In...Ch. 3.2 - Prob. 16ECh. 3.2 - Sketching Transformations of Monomial Functions In...Ch. 3.2 - Prob. 18ECh. 3.2 - Applying the Leading Coefficient Test In Exercises...Ch. 3.2 - Applying the Leading Coefficient Test In Exercises...Ch. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - In Exercises 33-48, (a) find all real zeros of the...Ch. 3.2 - In Exercises 33-48, (a) find all real zeros of the...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - In Exercises 53-62, find a polynomial function...Ch. 3.2 - Prob. 56ECh. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Prob. 58ECh. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Prob. 79ECh. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Prob. 81ECh. 3.2 - Prob. 82ECh. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Using Technology In Exercises 85-88, use a...Ch. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.2 - Prob. 89ECh. 3.2 - Using the Intermediate Value Theorem In Exercises...Ch. 3.2 - Prob. 91ECh. 3.2 - Prob. 92ECh. 3.2 - Maximum Volume You construct an open box from a...Ch. 3.2 - Maximum Volume You construct an open box with...Ch. 3.2 - Revenue The revenue R (in millions of dollars) for...Ch. 3.2 - Revenue The revenue R (in millions of dollars) for...Ch. 3.2 - Prob. 97ECh. 3.2 - Arboriculture The growth of a red oak tree is...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - Modeling Polynomials Sketch the graph of a...Ch. 3.2 - Modeling Polynomials Sketch the graph of a...Ch. 3.2 - Graphical Reasoning Sketch the graph of the...Ch. 3.2 - For each graph, describe a polynomial function...Ch. 3.2 - Prob. 107ECh. 3.3 - Divide the polynomial 9x3+36x249x196byx+4,and use...Ch. 3.3 - Divide x32x29byx3.Check the result.Ch. 3.3 - Prob. 3ECPCh. 3.3 - Prob. 4ECPCh. 3.3 - Prob. 5ECPCh. 3.3 - Prob. 6ECPCh. 3.3 - Two forms of the Division Algorithm are shown...Ch. 3.3 - In Exercises 2-6, fill in the blanks. In the...Ch. 3.3 - In Exercises 2-6, fill in the blanks. In the...Ch. 3.3 - In Exercises 2-6, fill in the blanks. A shortcut...Ch. 3.3 - In Exercises 2-6, fill in the blanks. The Theorem...Ch. 3.3 - In Exercises 2-6, fill in the blanks. The Theorem...Ch. 3.3 - Using the Division Algorithm In Exercises 7 and 8,...Ch. 3.3 - Using the Division Algorithm In Exercises 7 and 8,...Ch. 3.3 - Using Technology In Exercises 9 and 10, (a) use a...Ch. 3.3 - Prob. 10ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 14ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 16ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 18ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 20ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 22ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 24ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 28ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 30ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 32ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 34ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 36ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 38ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 40ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 42ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 44ECh. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Prob. 48ECh. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Prob. 50ECh. 3.3 - Using the Remainder Theorem In Exercises 51-54,...Ch. 3.3 - Prob. 52ECh. 3.3 - Using the Remainder Theorem In Exercises 51-54,...Ch. 3.3 - Prob. 54ECh. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Prob. 58ECh. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Prob. 60ECh. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Prob. 62ECh. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Prob. 64ECh. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Prob. 68ECh. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Prob. 70ECh. 3.3 - Approximating Zeros In Exercises 71-76, (a) use...Ch. 3.3 - Prob. 72ECh. 3.3 - Approximating Zeros In Exercises 71-76, (a) use...Ch. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - Prob. 77ECh. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Profit A company that produces calculators...Ch. 3.3 - Lyme Disease The numbers Nof confirmed cases of...Ch. 3.3 - True or False? In Exercises 83-86, determine...Ch. 3.3 - True or False? In Exercises 83-86, determine...Ch. 3.3 - True or False? In Exercises 83-86, determine...Ch. 3.3 - Prob. 86ECh. 3.3 - Think About It In Exercises 87 and 88, perform the...Ch. 3.3 - Think About It In Exercises 87 and 88, perform the...Ch. 3.3 - Error Analysis Describe the error. Use synthetic...Ch. 3.3 - HOW DO YOU SEE IT? The graph below shows a...Ch. 3.3 - Exploration In Exercises 91 and 92, find the...Ch. 3.3 - Exploration In Exercises 91 and 92, find the...Ch. 3.3 - Think About It Find the value of k such that x4is...Ch. 3.4 - Determine the number of zeros of the polynomial...Ch. 3.4 - Prob. 2ECPCh. 3.4 - Prob. 3ECPCh. 3.4 - Find the rational zeros of fx=2x3+x213x+6.Ch. 3.4 - Find all real solutions of 2x35x2+15x+18=0.Ch. 3.4 - Find a fourth-degree polynomial function f with...Ch. 3.4 - Find the quartic (fourth-degree) polynomial...Ch. 3.4 - Prob. 8ECPCh. 3.4 - Prob. 9ECPCh. 3.4 - Prob. 10ECPCh. 3.4 - Find all real zeros of fx=8x34x2+6x3.Ch. 3.4 - Prob. 12ECPCh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Zeros of Polynomial Functions In Exercises 9-14,...Ch. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Zeros of Polynomial Functions In Exercises 9-14,...Ch. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Using the Rational Zero Test In Exercises 15-18,...Ch. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Prob. 24ECh. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Solving a Polynomial Equation In Exercises 29-32,...Ch. 3.4 - Solving a Polynomial Equation In Exercises 29-32,...Ch. 3.4 - Prob. 32ECh. 3.4 - Using the Rational Zero Test In Exercises 33-36,...Ch. 3.4 - Using the Rational Zero Test In Exercises 33-36,...Ch. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Using the Rational Zero Test In Exercises 37-40,...Ch. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Prob. 42ECh. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Prob. 51ECh. 3.4 - Factoring a Polynomial In Exercises 51-54, write...Ch. 3.4 - Prob. 53ECh. 3.4 - Factoring a Polynomial In Exercises 51-54, write...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 57ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 59ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 61ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 63ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 65ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 67ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 69ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 73ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Using Descartes’s Rule of Signs In Exercises...Ch. 3.4 - Prob. 81ECh. 3.4 - Using Descartes’s Rule of Signs In Exercises...Ch. 3.4 - Prob. 83ECh. 3.4 - Using Descartes’s Rule of Signs In Exercises...Ch. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.4 - Prob. 101ECh. 3.4 - Prob. 102ECh. 3.4 - Geometry You want to make an open box from a...Ch. 3.4 - Geometry A rectangular package to be sent by a...Ch. 3.4 - Prob. 105ECh. 3.4 - Prob. 106ECh. 3.4 - Prob. 107ECh. 3.4 - Prob. 108ECh. 3.4 - Prob. 109ECh. 3.4 - Prob. 110ECh. 3.4 - Prob. 111ECh. 3.4 - Prob. 112ECh. 3.4 - Prob. 113ECh. 3.4 - Prob. 114ECh. 3.4 - Prob. 115ECh. 3.4 - Think About It Sketch the graph of a fifth-degree...Ch. 3.4 - Writing an Equation In Exercises 117 and 118, the...Ch. 3.4 - Prob. 118ECh. 3.4 - Prob. 119ECh. 3.4 - Prob. 120ECh. 3.4 - Prob. 121ECh. 3.4 - Prob. 122ECh. 3.4 - Prob. 123ECh. 3.5 - The ordered pairs below give the median sales...Ch. 3.5 - Prob. 2ECPCh. 3.5 - The simple interest on an investment is directly...Ch. 3.5 - Neglecting air resistance, the distance s an...Ch. 3.5 - Prob. 5ECPCh. 3.5 - The resistance of a copper wire carrying an...Ch. 3.5 - The kinetic energy E of an object varies jointly...Ch. 3.5 - Fill in the blanks. Two techniques for fitting...Ch. 3.5 - Fill in the blanks. Statisticians use a measure...Ch. 3.5 - Fill in the blanks. The linear model with the...Ch. 3.5 - Fill in the blanks. An r-value, or, of a set of...Ch. 3.5 - Fill in the blanks. The direct variation model...Ch. 3.5 - Fill in the blanks. The mathematical model y=2xis...Ch. 3.5 - Fill in the blanks. Mathematical models that...Ch. 3.5 - Fill in the blanks. The joint variation model...Ch. 3.5 - Mathematical Models In Exercises 9 and 10, (a)...Ch. 3.5 - Mathematical Models In Exercises 9 and 10, (a)...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Prob. 12ECh. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sports The ordered pairs below give the winning...Ch. 3.5 - Broadway The ordered pairs below give the starting...Ch. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Prob. 20ECh. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Prob. 22ECh. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Direct Variation as an nthPower In Exercises...Ch. 3.5 - Prob. 26ECh. 3.5 - Direct Variation as an nthPower In Exercises...Ch. 3.5 - Direct Variation as an nthPower In Exercises...Ch. 3.5 - Inverse Variation as an nth Power In Exercises...Ch. 3.5 - Prob. 30ECh. 3.5 - Inverse Variation as an nth Power In Exercises...Ch. 3.5 - Prob. 32ECh. 3.5 - Think About It In Exercises 33 and 34, use the...Ch. 3.5 - Think About It In Exercises 33 and 34, use the...Ch. 3.5 - Determining Variation In Exercises 35-38,...Ch. 3.5 - Prob. 36ECh. 3.5 - Determining Variation In Exercises 35-38,...Ch. 3.5 - Determining Variation In Exercises 35-38,...Ch. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 40ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 42ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 44ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 46ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Describing a Formula In Exercises 49-52, use...Ch. 3.5 - Prob. 50ECh. 3.5 - Describing a Formula In Exercises 49-52, use...Ch. 3.5 - Describing a Formula In Exercises 49-52, use...Ch. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 54ECh. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 56ECh. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 58ECh. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 60ECh. 3.5 - Simple Interest The simple interest on an...Ch. 3.5 - Prob. 62ECh. 3.5 - Measurement Use the fact that 13 inches is...Ch. 3.5 - Measurement Use the fact that 14 gallons is...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Ecology The diameter of the largest particle that...Ch. 3.5 - Work The work W required to lift an object varies...Ch. 3.5 - Prob. 71ECh. 3.5 - Prob. 72ECh. 3.5 - Music The fundamental frequency (in hertz) of a...Ch. 3.5 - Beam Load The maximum load that a horizontal beam...Ch. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - Prob. 77ECh. 3.5 - HOW DO YOU SEE IT? Discuss how well a linear model...Ch. 3.5 - Prob. 79ECh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Using Standard Form to Graph a Parabola In...Ch. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Geometry The perimeter of a rectangle is...Ch. 3 - Maximum Revenue The total revenue R earned (in...Ch. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Maximum Revenue A small theater has a seating...Ch. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Finding Real Zeros of a Polynomial Function In...Ch. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Using the Intermediate Value Theorem In Exercises...Ch. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Using the Intermediate Value Theorem In Exercises...Ch. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Using Synthetic Division In Exercises 57-60, use...Ch. 3 - Using Synthetic Division In Exercises 57-60, use...Ch. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Using the Rational Zero Test In Exercises 75-80,...Ch. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Using Descartes’s Rule of Signs In Exercises 93...Ch. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - Prob. 99RECh. 3 - Prob. 100RECh. 3 - Measurement A billboard says that it is 12.5 miles...Ch. 3 - Energy The power P produced by a wind turbine is...Ch. 3 - Frictional Force The frictional force F between...Ch. 3 - Demand A company has found that the daily demand x...Ch. 3 - Prob. 105RECh. 3 - Cost The cost of constructing a wooden box with a...Ch. 3 - Prob. 107RECh. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Prob. 110RECh. 3 - Writing Explain the connections between factors of...Ch. 3 - Prob. 1TCh. 3 - Prob. 2TCh. 3 - Write the standard form of the equation of the...Ch. 3 - The path of a ball is modeled by the function...Ch. 3 - Prob. 5TCh. 3 - Prob. 6TCh. 3 - Divide using synthetic division. 2x43x2+4x1x+2Ch. 3 - Use synthetic division to show that x=3 is a zero...Ch. 3 - In Exercises 9 and 10, find the rational zeros of...Ch. 3 - Prob. 10TCh. 3 - In Exercises 11 and 12, find a polynomial function...Ch. 3 - Prob. 12TCh. 3 - In Exercises 13 and 14, find all the zeros of the...Ch. 3 - In Exercises 13 and 14, find all the zeros of the...Ch. 3 - In Exercises 15-17, find a mathematical model that...Ch. 3 - In Exercises 15-17, find a mathematical model that...Ch. 3 - In Exercises 15-17, find a mathematical model that...Ch. 3 - Prob. 18TCh. 3 - Prob. 1PSCh. 3 - Prob. 2PSCh. 3 - Building a Quonset Hut Quonset huts were developed...Ch. 3 - Prob. 4PSCh. 3 - Prob. 5PSCh. 3 - Prob. 6PSCh. 3 - Sums and Products of Zeros (a) Complete the table....Ch. 3 - Prob. 8PSCh. 3 - Finding the Equation of a Parabola The parabola...Ch. 3 - Prob. 10PSCh. 3 - Prob. 11PSCh. 3 - Prob. 12PSCh. 3 - Finding Dimensions At a glassware factory, molten...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- If $8000 is deposited into an account earning simple interest at an annual interest rate of 4% for 10 years, howmuch interest was earned? Show you work.arrow_forward10-2 Let A = 02-4 and b = 4 Denote the columns of A by a₁, a2, a3, and let W = Span {a1, a2, a̸3}. -4 6 5 - 35 a. Is b in {a1, a2, a3}? How many vectors are in {a₁, a₂, a3}? b. Is b in W? How many vectors are in W? c. Show that a2 is in W. [Hint: Row operations are unnecessary.] a. Is b in {a₁, a2, a3}? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. ○ A. No, b is not in {a₁, a2, 3} since it cannot be generated by a linear combination of a₁, a2, and a3. B. No, b is not in (a1, a2, a3} since b is not equal to a₁, a2, or a3. C. Yes, b is in (a1, a2, a3} since b = a (Type a whole number.) D. Yes, b is in (a1, a2, 3} since, although b is not equal to a₁, a2, or a3, it can be expressed as a linear combination of them. In particular, b = + + ☐ az. (Simplify your answers.)arrow_forward14 14 4. The graph shows the printing rate of Printer A. Printer B can print at a rate of 25 pages per minute. How does the printing rate for Printer B compare to the printing rate for Printer A? The printing rate for Printer B is than the rate for Printer A because the rate of 25 pages per minute is than the rate of for Printer A. pages per minute RIJOUT 40 fy Printer Rat Number of Pages 8N WA 10 30 20 Printer A 0 0 246 Time (min) Xarrow_forward
- OR 16 f(x) = Ef 16 χ по x²-2 410 | y = (x+2) + 4 Y-INT: y = 0 X-INT: X=0 VA: x=2 OA: y=x+2 0 X-INT: X=-2 X-INT: y = 2 VA 0 2 whole. 2-2 4 y - (x+2) = 27-270 + xxx> 2 क् above OA (x+2) OA x-2/x²+0x+0 2 x-2x 2x+O 2x-4 4 X<-1000 4/4/2<0 below Of y VA X=2 X-2 OA y=x+2 -2 2 (0,0) 2 χarrow_forwardI need help solving the equation 3x+5=8arrow_forwardWhat is the domain, range, increasing intervals (theres 3), decreasing intervals, roots, y-intercepts, end behavior (approaches four times), leading coffiencent status (is it negative, positivie?) the degress status (zero, undifined etc ), the absolute max, is there a absolute minimum, relative minimum, relative maximum, the root is that has a multiplicity of 2, the multiplicity of 3.arrow_forward
- What is the vertex, axis of symmerty, all of the solutions, all of the end behaviors, the increasing interval, the decreasing interval, describe all of the transformations that have occurred EXAMPLE Vertical shrink/compression (wider). or Vertical translation down, the domain and range of this graph EXAMPLE Domain: x ≤ -1 Range: y ≥ -4.arrow_forward4. Select all of the solutions for x²+x - 12 = 0? A. -12 B. -4 C. -3 D. 3 E 4 F 12 4 of 10arrow_forward2. Select all of the polynomials with the degree of 7. A. h(x) = (4x + 2)³(x − 7)(3x + 1)4 B h(x) = (x + 7)³(2x + 1)^(6x − 5)² ☐ Ch(x)=(3x² + 9)(x + 4)(8x + 2)ª h(x) = (x + 6)²(9x + 2) (x − 3) h(x)=(-x-7)² (x + 8)²(7x + 4)³ Scroll down to see more 2 of 10arrow_forward
- 1. If all of the zeros for a polynomial are included in the graph, which polynomial could the graph represent? 100 -6 -2 0 2 100 200arrow_forward3. Select the polynomial that matches the description given: Zero at 4 with multiplicity 3 Zero at −1 with multiplicity 2 Zero at -10 with multiplicity 1 Zero at 5 with multiplicity 5 ○ A. P(x) = (x − 4)³(x + 1)²(x + 10)(x — 5)³ B - P(x) = (x + 4)³(x − 1)²(x − 10)(x + 5)³ ○ ° P(x) = (1 − 3)'(x + 2)(x + 1)"'" (x — 5)³ 51 P(r) = (x-4)³(x − 1)(x + 10)(x − 5 3 of 10arrow_forwardMatch the equation, graph, and description of transformation. Horizontal translation 1 unit right; vertical translation 1 unit up; vertical shrink of 1/2; reflection across the x axis Horizontal translation 1 unit left; vertical translation 1 unit down; vertical stretch of 2 Horizontal translation 2 units right; reflection across the x-axis Vertical translation 1 unit up; vertical stretch of 2; reflection across the x-axis Reflection across the x - axis; vertical translation 2 units down Horizontal translation 2 units left Horizontal translation 2 units right Vertical translation 1 unit down; vertical shrink of 1/2; reflection across the x-axis Vertical translation 2 units down Horizontal translation 1 unit left; vertical translation 2 units up; vertical stretch of 2; reflection across the x - axis f(x) = - =-½ ½ (x − 1)²+1 f(x) = x²-2 f(x) = -2(x+1)²+2 f(x)=2(x+1)²-1 f(x)=-(x-2)² f(x)=(x-2)² f(x) = f(x) = -2x²+1 f(x) = -x²-2 f(x) = (x+2)²arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY