Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)

4th Edition

ISBN: 9780133178579

Author: Ross L. Finney

Publisher: PEARSON

See similar textbooks

Concept explainers

Limits

When it comes to calculus, limits are considered to be a very important topic of discussion. The main importance of limit lies in expressing the value of a function as it gets closer to a certain value. Also, limits can help you to understand other topic…

Videos

Question

Chapter 3.2, Problem 6E

(a)

To determine

The domain points of the given function appear to be differentiable.

(a)

Expert Solution

Answer to Problem 6E

The required domain points of the given function appears to be differentiable is [−2,3] .

Explanation of Solution

Given information:

The given function is: y=f(x) .

And, the domain points is D:−2≤x≤3

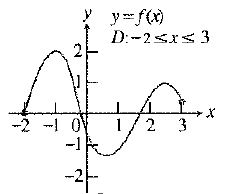
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 3.2, Problem 6E , additional homework tip 1

The given function is: y=f(x) .and the domain points is D:−3≤x≤3 .

Since, from the figure it is seen that the function y=f(x) is continuous in the given domain D:−2≤x≤3 .

Also, there are no vertical tangents, corners, or cusps.

Thus, the function y=f(x) is differentiable at all points in its domain which is [−2,3]

Hence, the required domain of the function appears to be differentiable is [−2,3] .

(b)

To determine

The domain points of the given function appear to be continuous but not differentiable.

(b)

Expert Solution

Answer to Problem 6E

The required domain of the given function appears to be continuous but not differentiable is none.

Explanation of Solution

Given information:

The given function is: y=f(x) .

And, the domain points is D:−2≤x≤3

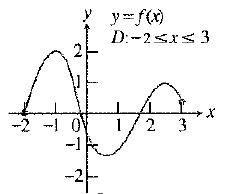
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 3.2, Problem 6E , additional homework tip 2

The given function is: y=f(x) .and the domain points is D:−2≤x≤3 .

From the results (a) it is seen that the function y=f(x) is differentiable at all points in its domain. As it is also continuous on its domain.

Thus, there are no points where it is continuous but not differentiable.

Hence, the required domain of the function whether the function appears to be continuous but not differentiable is none.

(c)

To determine

The domain of the given function appear neither continuous nor differentiable.

(c)

Expert Solution

Answer to Problem 6E

The required domain of the given function appears to be neither continuous nor differentiable is none.

Explanation of Solution

Given information:

The given function is: y=f(x) .

And, the domain points is D:−2≤x≤3

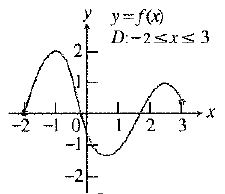
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 3.2, Problem 6E , additional homework tip 3

The given function is: y=f(x) .and the domain points is D:−2≤x≤3 .

From the results (a) the function is shown to be differentiable in its domain at all points. And it is also continuous on its domain.

So, there are no points where the given function appears neither continuous nor differentiable.

Hence, the required domain of the given function appears neither continuous nor differentiable.

Chapter 3.2, Problem 5E

Chapter 3.2, Problem 7E

Chapter 3 Solutions

Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)

Ch. 3.1 - Prob. 1QR Ch. 3.1 - Prob. 2QR Ch. 3.1 - Prob. 3QR Ch. 3.1 - Prob. 4QR Ch. 3.1 - Prob. 5QR Ch. 3.1 - Prob. 6QR Ch. 3.1 - Prob. 7QR Ch. 3.1 - Prob. 8QR Ch. 3.1 - Prob. 9QR Ch. 3.1 - Prob. 10QR

Ch. 3.1 - Prob. 1E Ch. 3.1 - Prob. 2E Ch. 3.1 - Prob. 3E Ch. 3.1 - Prob. 4E Ch. 3.1 - Prob. 5E Ch. 3.1 - Prob. 6E Ch. 3.1 - Prob. 7E Ch. 3.1 - Prob. 8E Ch. 3.1 - Prob. 9E Ch. 3.1 - Prob. 10E Ch. 3.1 - Prob. 11E Ch. 3.1 - Prob. 12E Ch. 3.1 - Prob. 13E Ch. 3.1 - Prob. 14E Ch. 3.1 - Prob. 15E Ch. 3.1 - Prob. 16E Ch. 3.1 - Prob. 17E Ch. 3.1 - Prob. 18E Ch. 3.1 - Prob. 19E Ch. 3.1 - Prob. 20E Ch. 3.1 - Prob. 21E Ch. 3.1 - Prob. 22E Ch. 3.1 - Prob. 23E Ch. 3.1 - Prob. 24E Ch. 3.1 - Prob. 25E Ch. 3.1 - Prob. 26E Ch. 3.1 - Prob. 27E Ch. 3.1 - Prob. 28E Ch. 3.1 - Prob. 29E Ch. 3.1 - Prob. 30E Ch. 3.1 - Prob. 31E Ch. 3.1 - Prob. 32E Ch. 3.1 - Prob. 33E Ch. 3.1 - Prob. 34E Ch. 3.1 - Prob. 35E Ch. 3.1 - Prob. 36E Ch. 3.1 - Prob. 37E Ch. 3.1 - Prob. 38E Ch. 3.1 - Prob. 39E Ch. 3.1 - Prob. 40E Ch. 3.1 - Prob. 41E Ch. 3.1 - Prob. 42E Ch. 3.1 - Prob. 43E Ch. 3.1 - Prob. 44E Ch. 3.1 - Prob. 45E Ch. 3.2 - Prob. 1QR Ch. 3.2 - Prob. 2QR Ch. 3.2 - Prob. 3QR Ch. 3.2 - Prob. 4QR Ch. 3.2 - Prob. 5QR Ch. 3.2 - Prob. 6QR Ch. 3.2 - Prob. 7QR Ch. 3.2 - Prob. 8QR Ch. 3.2 - Prob. 9QR Ch. 3.2 - Prob. 10QR Ch. 3.2 - Prob. 1E Ch. 3.2 - Prob. 2E Ch. 3.2 - Prob. 3E Ch. 3.2 - Prob. 4E Ch. 3.2 - Prob. 5E Ch. 3.2 - Prob. 6E Ch. 3.2 - Prob. 7E Ch. 3.2 - Prob. 8E Ch. 3.2 - Prob. 9E Ch. 3.2 - Prob. 10E Ch. 3.2 - Prob. 11E Ch. 3.2 - Prob. 12E Ch. 3.2 - Prob. 13E Ch. 3.2 - Prob. 14E Ch. 3.2 - Prob. 15E Ch. 3.2 - Prob. 16E Ch. 3.2 - Prob. 17E Ch. 3.2 - Prob. 18E Ch. 3.2 - Prob. 19E Ch. 3.2 - Prob. 20E Ch. 3.2 - Prob. 21E Ch. 3.2 - Prob. 22E Ch. 3.2 - Prob. 23E Ch. 3.2 - Prob. 24E Ch. 3.2 - Prob. 25E Ch. 3.2 - Prob. 26E Ch. 3.2 - Prob. 27E Ch. 3.2 - Prob. 28E Ch. 3.2 - Prob. 29E Ch. 3.2 - Prob. 30E Ch. 3.2 - Prob. 31E Ch. 3.2 - Prob. 32E Ch. 3.2 - Prob. 33E Ch. 3.2 - Prob. 34E Ch. 3.2 - Prob. 35E Ch. 3.2 - Prob. 36E Ch. 3.2 - Prob. 37E Ch. 3.2 - Prob. 38E Ch. 3.2 - Prob. 39E Ch. 3.2 - Prob. 40E Ch. 3.2 - Prob. 41E Ch. 3.2 - Prob. 42E Ch. 3.2 - Prob. 43E Ch. 3.2 - Prob. 44E Ch. 3.2 - Prob. 45E Ch. 3.2 - Prob. 46E Ch. 3.2 - Prob. 47E Ch. 3.2 - Prob. 48E Ch. 3.3 - Prob. 1QR Ch. 3.3 - Prob. 2QR Ch. 3.3 - Prob. 3QR Ch. 3.3 - Prob. 4QR Ch. 3.3 - Prob. 5QR Ch. 3.3 - Prob. 6QR Ch. 3.3 - Prob. 7QR Ch. 3.3 - Prob. 8QR Ch. 3.3 - Prob. 9QR Ch. 3.3 - Prob. 10QR Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.3 - Prob. 9E Ch. 3.3 - Prob. 10E Ch. 3.3 - Prob. 11E Ch. 3.3 - Prob. 12E Ch. 3.3 - Prob. 13E Ch. 3.3 - Prob. 14E Ch. 3.3 - Prob. 15E Ch. 3.3 - Prob. 16E Ch. 3.3 - Prob. 17E Ch. 3.3 - Prob. 18E Ch. 3.3 - Prob. 19E Ch. 3.3 - Prob. 20E Ch. 3.3 - Prob. 21E Ch. 3.3 - Prob. 22E Ch. 3.3 - Prob. 23E Ch. 3.3 - Prob. 24E Ch. 3.3 - Prob. 25E Ch. 3.3 - Prob. 26E Ch. 3.3 - Prob. 27E Ch. 3.3 - Prob. 28E Ch. 3.3 - Prob. 29E Ch. 3.3 - Prob. 30E Ch. 3.3 - Prob. 31E Ch. 3.3 - Prob. 32E Ch. 3.3 - Prob. 33E Ch. 3.3 - Prob. 34E Ch. 3.3 - Prob. 35E Ch. 3.3 - Prob. 36E Ch. 3.3 - Prob. 37E Ch. 3.3 - Prob. 38E Ch. 3.3 - Prob. 39E Ch. 3.3 - Prob. 40E Ch. 3.3 - Prob. 41E Ch. 3.3 - Prob. 42E Ch. 3.3 - Prob. 43E Ch. 3.3 - Prob. 44E Ch. 3.3 - Prob. 45E Ch. 3.3 - Prob. 46E Ch. 3.3 - Prob. 47E Ch. 3.3 - Prob. 48E Ch. 3.3 - Prob. 49E Ch. 3.3 - Prob. 50E Ch. 3.3 - Prob. 51E Ch. 3.3 - Prob. 52E Ch. 3.3 - Prob. 53E Ch. 3.3 - Prob. 54E Ch. 3.3 - Prob. 55E Ch. 3.3 - Prob. 56E Ch. 3.3 - Prob. 57E Ch. 3.3 - Prob. 58E Ch. 3.3 - Prob. 59E Ch. 3.3 - Prob. 1QQ Ch. 3.3 - Prob. 2QQ Ch. 3.3 - Prob. 3QQ Ch. 3.3 - Prob. 4QQ Ch. 3.4 - Prob. 1QR Ch. 3.4 - Prob. 2QR Ch. 3.4 - Prob. 3QR Ch. 3.4 - Prob. 4QR Ch. 3.4 - Prob. 5QR Ch. 3.4 - Prob. 6QR Ch. 3.4 - Prob. 7QR Ch. 3.4 - Prob. 8QR Ch. 3.4 - Prob. 9QR Ch. 3.4 - Prob. 10QR Ch. 3.4 - Prob. 1E Ch. 3.4 - Prob. 2E Ch. 3.4 - Prob. 3E Ch. 3.4 - Prob. 4E Ch. 3.4 - Prob. 5E Ch. 3.4 - Prob. 6E Ch. 3.4 - Prob. 7E Ch. 3.4 - Prob. 8E Ch. 3.4 - Prob. 9E Ch. 3.4 - Prob. 10E Ch. 3.4 - Prob. 11E Ch. 3.4 - Prob. 12E Ch. 3.4 - Prob. 13E Ch. 3.4 - Prob. 14E Ch. 3.4 - Prob. 15E Ch. 3.4 - Prob. 16E Ch. 3.4 - Prob. 17E Ch. 3.4 - Prob. 18E Ch. 3.4 - Prob. 19E Ch. 3.4 - Prob. 20E Ch. 3.4 - Prob. 21E Ch. 3.4 - Prob. 22E Ch. 3.4 - Prob. 23E Ch. 3.4 - Prob. 24E Ch. 3.4 - Prob. 25E Ch. 3.4 - Prob. 26E Ch. 3.4 - Prob. 27E Ch. 3.4 - Prob. 28E Ch. 3.4 - Prob. 29E Ch. 3.4 - Prob. 30E Ch. 3.4 - Prob. 31E Ch. 3.4 - Prob. 32E Ch. 3.4 - Prob. 33E Ch. 3.4 - Prob. 34E Ch. 3.4 - Prob. 35E Ch. 3.4 - Prob. 36E Ch. 3.4 - Prob. 37E Ch. 3.4 - Prob. 38E Ch. 3.4 - Prob. 39E Ch. 3.4 - Prob. 40E Ch. 3.4 - Prob. 41E Ch. 3.4 - Prob. 42E Ch. 3.4 - Prob. 43E Ch. 3.4 - Prob. 44E Ch. 3.4 - Prob. 45E Ch. 3.4 - Prob. 46E Ch. 3.4 - Prob. 47E Ch. 3.4 - Prob. 48E Ch. 3.4 - Prob. 49E Ch. 3.4 - Prob. 50E Ch. 3.5 - Prob. 1QR Ch. 3.5 - Prob. 2QR Ch. 3.5 - Prob. 3QR Ch. 3.5 - Prob. 4QR Ch. 3.5 - Prob. 5QR Ch. 3.5 - Prob. 6QR Ch. 3.5 - Prob. 7QR Ch. 3.5 - Prob. 8QR Ch. 3.5 - Prob. 9QR Ch. 3.5 - Prob. 10QR Ch. 3.5 - Prob. 1E Ch. 3.5 - Prob. 2E Ch. 3.5 - Prob. 3E Ch. 3.5 - Prob. 4E Ch. 3.5 - Prob. 5E Ch. 3.5 - Prob. 6E Ch. 3.5 - Prob. 7E Ch. 3.5 - Prob. 8E Ch. 3.5 - Prob. 9E Ch. 3.5 - Prob. 10E Ch. 3.5 - Prob. 11E Ch. 3.5 - Prob. 12E Ch. 3.5 - Prob. 13E Ch. 3.5 - Prob. 14E Ch. 3.5 - Prob. 15E Ch. 3.5 - Prob. 16E Ch. 3.5 - Prob. 17E Ch. 3.5 - Prob. 18E Ch. 3.5 - Prob. 19E Ch. 3.5 - Prob. 20E Ch. 3.5 - Prob. 21E Ch. 3.5 - Prob. 22E Ch. 3.5 - Prob. 23E Ch. 3.5 - Prob. 24E Ch. 3.5 - Prob. 25E Ch. 3.5 - Prob. 26E Ch. 3.5 - Prob. 27E Ch. 3.5 - Prob. 28E Ch. 3.5 - Prob. 29E Ch. 3.5 - Prob. 30E Ch. 3.5 - Prob. 31E Ch. 3.5 - Prob. 32E Ch. 3.5 - Prob. 33E Ch. 3.5 - Prob. 34E Ch. 3.5 - Prob. 35E Ch. 3.5 - Prob. 36E Ch. 3.5 - Prob. 37E Ch. 3.5 - Prob. 38E Ch. 3.5 - Prob. 39E Ch. 3.5 - Prob. 40E Ch. 3.5 - Prob. 41E Ch. 3.5 - Prob. 42E Ch. 3.5 - Prob. 43E Ch. 3.5 - Prob. 44E Ch. 3.5 - Prob. 45E Ch. 3.5 - Prob. 46E Ch. 3.5 - Prob. 47E Ch. 3.5 - Prob. 48E Ch. 3.5 - Prob. 49E Ch. 3.5 - Prob. 50E Ch. 3.5 - Prob. 51E Ch. 3.5 - Prob. 52E Ch. 3.5 - Prob. 1QQ Ch. 3.5 - Prob. 2QQ Ch. 3.5 - Prob. 3QQ Ch. 3.5 - Prob. 4QQ Ch. 3 - Prob. 1RE Ch. 3 - Prob. 2RE Ch. 3 - Prob. 3RE Ch. 3 - Prob. 4RE Ch. 3 - Prob. 5RE Ch. 3 - Prob. 6RE Ch. 3 - Prob. 7RE Ch. 3 - Prob. 8RE Ch. 3 - Prob. 9RE Ch. 3 - Prob. 10RE Ch. 3 - Prob. 11RE Ch. 3 - Prob. 12RE Ch. 3 - Prob. 13RE Ch. 3 - Prob. 14RE Ch. 3 - Prob. 15RE Ch. 3 - Prob. 16RE Ch. 3 - Prob. 17RE Ch. 3 - Prob. 18RE Ch. 3 - Prob. 19RE Ch. 3 - Prob. 20RE Ch. 3 - Prob. 21RE Ch. 3 - Prob. 22RE Ch. 3 - Prob. 23RE Ch. 3 - Prob. 24RE Ch. 3 - Prob. 25RE Ch. 3 - Prob. 26RE Ch. 3 - Prob. 27RE Ch. 3 - Prob. 28RE Ch. 3 - Prob. 29RE Ch. 3 - Prob. 30RE Ch. 3 - Prob. 31RE Ch. 3 - Prob. 32RE Ch. 3 - Prob. 33RE Ch. 3 - Prob. 34RE Ch. 3 - Prob. 35RE Ch. 3 - Prob. 36RE Ch. 3 - Prob. 37RE Ch. 3 - Prob. 38RE Ch. 3 - Prob. 39RE Ch. 3 - Prob. 40RE Ch. 3 - Prob. 41RE Ch. 3 - Prob. 42RE Ch. 3 - Prob. 43RE Ch. 3 - Prob. 44RE Ch. 3 - Prob. 45RE Ch. 3 - Prob. 46RE Ch. 3 - Prob. 47RE Ch. 3 - Prob. 48RE Ch. 3 - Prob. 49RE Ch. 3 - Prob. 50RE Ch. 3 - Prob. 51RE Ch. 3 - Prob. 52RE Ch. 3 - Prob. 53RE Ch. 3 - Prob. 54RE Ch. 3 - Prob. 55RE Ch. 3 - Prob. 56RE Ch. 3 - Prob. 57RE Ch. 3 - Prob. 58RE Ch. 3 - Prob. 59RE Ch. 3 - Prob. 60RE Ch. 3 - Prob. 61RE Ch. 3 - Prob. 62RE Ch. 3 - Prob. 63RE Ch. 3 - Prob. 64RE Ch. 3 - Prob. 65RE Ch. 3 - Prob. 66RE Ch. 3 - Prob. 67RE Ch. 3 - Prob. 68RE Ch. 3 - Prob. 69RE Ch. 3 - Prob. 70RE Ch. 3 - Prob. 71RE Ch. 3 - Prob. 72RE Ch. 3 - Prob. 73RE Ch. 3 - Prob. 74RE Ch. 3 - Prob. 75RE Ch. 3 - Prob. 76RE Ch. 3 - Prob. 77RE Ch. 3 - Prob. 78RE Ch. 3 - Prob. 79RE Ch. 3 - Prob. 80RE Ch. 3 - Prob. 81RE Ch. 3 - Prob. 82RE Ch. 3 - Prob. 83RE

Additional Math Textbook Solutions

Find more solutions based on key concepts

For a population containing N=902 individual, what code number would you assign for a. the first person on the ...

Basic Business Statistics, Student Value Edition

In Exercises 3–8, find the limit of each function (a) as, and (b) as . (You may wish to visualize your answer ...

University Calculus: Early Transcendentals (4th Edition)

Applying the Empirical Rule with z-Scores The Empirical Rule applies rough approximations to probabilities for ...

Introductory Statistics

Testing Claims About Proportions. In Exercises 9–32, test the given claim. Identify the null hypothesis, altern...

Elementary Statistics (13th Edition)

In Problems 11-22, draw each angle in standard position. 6

Precalculus

The equation for the given sequence and to find the indicated term. 3,8,13,18...; 20th term.

Pre-Algebra Student Edition

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.

The domain points of the given function appear to be differentiable .

Concept explainers

Videos

The domain points of the given function appear to be differentiable.

Answer to Problem 6E

Explanation of Solution

The domain points of the given function appear to be continuous but not differentiable.

Answer to Problem 6E

Explanation of Solution

The domain of the given function appear neither continuous nor differentiable.

Answer to Problem 6E

Explanation of Solution

Chapter 3 Solutions

Additional Math Textbook Solutions