Chapter 32, Problem 32.70AP

At t = 0, the open switch in Figure P31.46 is thrown closed. We wish to find a symbolic expression for the current in the inductor for time t > 0. Let this current be called i and choose it to be downward in the inductor in Figure P31.46. Identify i₁ as the current to the right through R₁ and i₂ as the current downward through R₂. (a) Use Kirchhoff’s junction rule to find a relation among the three currents. (b) Use Kirchhoff’s loop rule around the left loop to find another relationship. (c) Use Kirchhoff’s loop rule around the outer loop to find a third relationship. (d) Eliminate i₁ and i₂ among the three equations to find an equation involving only the current i. (e) Compare the equation in part (d) with Equation 31.6 in the text. Use this comparison to rewrite Equation 31.7 in the text for the situation in this problem and show that

$i(t)=\frac{\epsilon }{R_1}[1-e^{-(R^{\prime }/L)t}]$

where R′ = R₁R₂/(R₁ + R₂).

Figure P31.46

To determine

The relation among the three currents by Kirchhoff’s junction rule.

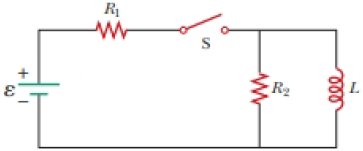
Answer to Problem 32.70AP

The relation among the three currents by Kirchhoff’s junction rule are $i_1=i_2+i$.

Explanation of Solution

Given info: The figure that shows the given circuit is shown below.

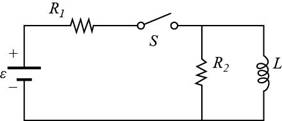
Figure (I)

According to Kirchhoff’s junction rule, the total incoming currents are equal to the total outgoing currents at a junction.

From the circuit diagram equating the incoming currents to the outgoing current,

$i_1=i_2+i$

Here,

$i_1$ is the current flow through the resistance $R_1$.

$i_2$ is the current flow through the resistance $R_2$.

$i$ is the current flow through the inductor.

Conclusion:

Therefore, the relation among three currents by Kirchhoff’s junction rule are $i_1=i_2+i$.

To determine

The relationship between the given variables around the left loop by Kirchhoff’s loop rule.

Answer to Problem 32.70AP

The relationship between the given variables around the left loop by Kirchhoff’s loop rule is $\epsilon -i_1{R}_1-i_2{R}_2=0$.

Explanation of Solution

Given info: The figure that shows the given circuit is shown in figure (I).

According to Kirchhoff’s loop rule, the sum of all the voltage across all the elements in a loop must be zero.

From the circuit diagram equating the voltage across the elements in the left loop is equal to zero.

$\epsilon -i_1{R}_1-i_2{R}_2=0$ (1)

Here,

$\epsilon$ is the emf of the battery.

Conclusion:

Therefore, the relationship between the given variables around the left loop by Kirchhoff’s loop rule is $\epsilon -i_1{R}_1-i_2{R}_2=0$.

To determine

The relationship between the given variables around the outer loop by Kirchhoff’s loop rule.

Answer to Problem 32.70AP

The relationship between the given variables around the outer loop by Kirchhoff’s loop rule is $\epsilon -i_1{R}_1-L\frac{di}{dt}=0$.

Explanation of Solution

Given info: The figure that shows the given circuit is shown in figure (I).

According to Kirchhoff’s loop rule, the sum of all the voltage across all the elements in a loop must be zero.

From the circuit diagram equating the voltage across the elements in the outer loop is equal to zero.

$\epsilon -i_1{R}_1-L\frac{di}{dt}=0$ (2)

Conclusion:

Therefore, the relationship between the given variables around the outer loop by Kirchhoff’s loop rule is $\epsilon -i_1{R}_1-L\frac{di}{dt}=0$.

To determine

The equation that involve only current $i$

Answer to Problem 32.70AP

The equation that involve only current $i$ is $\epsilon \text{'}-iR\text{'}-L\frac{di}{dt}=0$.

Explanation of Solution

Given info: The figure that shows the given circuit is shown in figure (I).

From equation (1), the expression for the

$\epsilon -i_1{R}_1-i_2{R}_2=0$

Substitute $i_2+i$ for $i_1$ in above equation and rearrange for $i_2$.

$\begin{array}{c}\epsilon -\left(i_2+i\right)R_1-i_2{R}_2=0\\ i_2{R}_1+i{R}_1+i_2{R}_2=\epsilon \\ i_2\left(R_1+R_2\right)=\epsilon -i{R}_1\\ i_2=\frac{\epsilon -i{R}_1}{R_1+R_2}\end{array}$ (3)

From equation (2), the expression for the

$\epsilon -i_1{R}_1-L\frac{di}{dt}=0$

Substitute $i_2+i$ for $i_1$ in above equation and rearrange for $i_2$.

$\begin{array}{c}\epsilon -\left(i_2+i\right)R_1-L\frac{di}{dt}=0\\ \left(i_2+i\right)R_1+L\frac{di}{dt}=\epsilon \\ \left(i_2+i\right)=\frac{\epsilon -L\frac{di}{dt}}{R_1}\\ i_2=\frac{\epsilon -L\frac{di}{dt}}{R_1}-i\end{array}$ (4)

Equate equation (3) and equation (4) for $i_2$.

$\begin{array}{c}\frac{\epsilon -L\frac{di}{dt}}{R_1}-i=\frac{\epsilon -i{R}_1}{R_1+R_2}\\ \left(\frac{\epsilon -i{R}_1}{R_1+R_2}+i\right)R_1=\epsilon -L\frac{di}{dt}\\ \left(\frac{\epsilon -i{R}_1+\left(R_1+R_2\right)i}{R_1+R_2}\right)R_1=\epsilon -L\frac{di}{dt}\\ \left(\frac{\epsilon +i{R}_2}{R_1+R_2}\right)R_1=\epsilon -L\frac{di}{dt}\end{array}$

Further solve the above equation,

$\begin{array}{c}\epsilon -\left(\frac{\epsilon +i{R}_2}{R_1+R_2}\right)R_1=L\frac{di}{dt}\\ \frac{\epsilon \left(R_1+R_2\right)-\left(\epsilon +i{R}_2\right)R_1}{R_1+R_2}=L\frac{di}{dt}\\ \frac{\epsilon R_2-i{R}_1{R}_2}{R_1+R_2}=L\frac{di}{dt}\\ \epsilon \left(\frac{R_2}{R_1+R_2}\right)-i\left(\frac{R_1{R}_2}{R_1+R_2}\right)-L\frac{di}{dt}=0\end{array}$

Assume $\epsilon \text{'}=\epsilon \left(\frac{R_2}{R_1+R_2}\right)$ and $R\text{'}=\left(\frac{R_1{R}_2}{R_1+R_2}\right)$.

Substitute $\epsilon \text{'}$ for $\epsilon \left(\frac{R_2}{R_1+R_2}\right)$ and $R\text{'}$ for $\left(\frac{R_1{R}_2}{R_1+R_2}\right)$ in equation ().

$\epsilon \text{'}-iR\text{'}-L\frac{di}{dt}=0$

Thus, the require equation in term of current $i$ is $\epsilon \text{'}-iR\text{'}-L\frac{di}{dt}=0$.

Conclusion:

Therefore, the equation that involve only current $i$ is $\epsilon \text{'}-iR\text{'}-L\frac{di}{dt}=0$.

To determine

The comparison of equation for part (d) with the equation $31.6$ in the text use this comparison rewrite the equation $31.7$ in the text for the text and show that $i\left(t\right)=\frac{\epsilon }{R_1}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$

Answer to Problem 32.70AP

The equation $31.6$ in the text and the equation in part (d) are similar also the equation 31.7 can be rewrite for this situation is $i\left(t\right)=\frac{\epsilon \text{'}}{R\text{'}}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$ and it showed that $i\left(t\right)=\frac{\epsilon }{R_1}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$.

Explanation of Solution

From the textbook the equation $31.6$ is given as,

$\epsilon -iR-L\frac{di}{dt}=0$

From the part (d), the equation is given as,

$\epsilon \text{'}-iR\text{'}-L\frac{di}{dt}=0$

Since both the equation shown above are same therefore their solution are also same.

The solution of the equation $31.6$ is given in the text as equation $31.7$ that is,

$i\left(t\right)=\frac{\epsilon }{R_1}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$

Similarly rewrite the equation $31.7$ for the part (d) equation.

$i\left(t\right)=\frac{\epsilon \text{'}}{R\text{'}}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$

Substitute $\epsilon \text{'}$ for $\epsilon \left(\frac{R_2}{R_1+R_2}\right)$ and $R\text{'}$ for $\left(\frac{R_1{R}_2}{R_1+R_2}\right)$ in equation ().

$\begin{array}{l}i\left(t\right)=\frac{\left(\epsilon \left(\frac{R_2}{R_1+R_2}\right)\right)}{\left(\left(\frac{R_1{R}_2}{R_1+R_2}\right)\right)}\left[1-e^{-\left(R\text{'}/L\right)t}\right]\\ i\left(t\right)=\frac{\epsilon }{R_1}\left[1-e^{-\left(R\text{'}/L\right)t}\right]\end{array}$

Conclusion:

Therefore, the equation $31.6$ in the text and the equation in part (d) are similar also the equation 31.7 can be rewrite for this situation is $i\left(t\right)=\frac{\epsilon \text{'}}{R\text{'}}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$ and it showed that $i\left(t\right)=\frac{\epsilon }{R_1}\left[1-e^{-\left(R\text{'}/L\right)t}\right]$.