
(a)
The current in the inductor as a function of time.
(a)
Answer to Problem 26P
The current in the inductor as a function of time is
Explanation of Solution
Write the expression based on junction rule.
Here,
Write the expression to obtain the loop rule.
Here,
Write the expression to obtain the current in the circuit.
Here, current in the circuit is
The current flow in the circuit is as shown in the figure below.
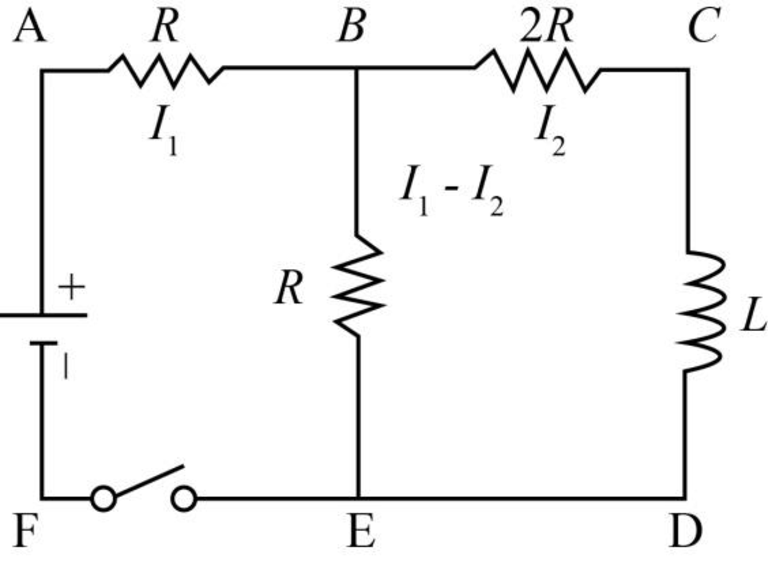
Figure-(1)
Write the expression to obtain the voltage the loop
Here,
Write the expression to obtain the loop
Here,
Re-write the above equation.
Substitute
Further solve the above equation.
The general solution of the linear differential equation.
Here,
Substitute
Substitute
Substitute
Conclusion:
Substitute
Therefore, the current in the inductor as a function of time is
(b)
The current in the switch as a function of time.
(b)
Answer to Problem 26P
The current in the switch as a function of time is
Explanation of Solution
Consider equation (II) to obtain the current in the switch as a function of time.
Substitute
Further substitute
Conclusion:
Substitute
Therefore, the current in the switch as a function of time is
Want to see more full solutions like this?
Chapter 32 Solutions
Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
- Plastic beads can often carry a small charge and therefore can generate electric fields. Three beads are oriented such that system of all three beads is zero. 91 E field lines 93 92 What charge does each bead carry? 91 92 -1.45 = = What is the net charge of the system? What charges have to be equal? μC 2.9 × What is the net charge of the system? What charges have to be equal? μC 93 = 2.9 μС 92 is between and 91 93° The sum of the charge on q₁ and 92 is 91 + 92 = −2.9 μC, and the net charge of thearrow_forwardPlastic beads can often carry a small charge and therefore can generate electric fields. Three beads are oriented such that 92 is between q₁ and 93. The sum of the charge on 9₁ and 92 is 9₁ + 92 = −2.9 µС, and the net charge of the system of all three beads is zero. E field lines 93 92 What charge does each bead carry? 91 92 -1.45 What is the net charge of the system? What charges have to be equal? μC 2.9 ✓ What is the net charge of the system? What charges have to be equal? μC 93 2.9 μεarrow_forwardNo chatgpt pls will upvotearrow_forward
- Point charges of 6.50 μC and -2.50 μC are placed 0.300 m apart. (Assume the negative charge is located to the right of the positive charge. Include the sign of the value in your answers.) (a) Where can a third charge be placed so that the net force on it is zero? 0.49 m to the right of the -2.50 μC charge (b) What if both charges are positive? 0.49 xm to the right of the 2.50 μC chargearrow_forwardFind the electric field at the location of q, in the figure below, given that q₁ =9c9d = +4.60 nC, q = -1.00 nC, and the square is 20.0 cm on a side. (The +x axis is directed to the right.) magnitude direction 2500 x What symmetries can you take advantage of? What charges are the same magnitude and the same distance away? N/C 226 × How does charge sign affect the direction of the electric field? counterclockwise from the +x-axis 9a 9b % 9 9darrow_forwardwould 0.215 be the answer for part b?arrow_forward
- Suppose a toy boat moves in a pool at at a speed given by v=1.0 meter per second at t=0, and that the boat is subject to viscous damping. The damping on the boat causes the rate of speed loss to be given by the expression dv/dt=-2v. How fast will the boat be traveling after 1 second? 3 seconds? 10 seconds? Use separation of variables to solve this.arrow_forwardWhat functional form do you expect to describe the motion of a vibrating membrane without damping and why?arrow_forwardIf speed is tripled, how much larger will air drag become for an object? Show the math.arrow_forward
- What does it tell us about factors on which air drag depends if it is proportional to speed squared?arrow_forwardWhat is the net charge on a sphere that has the following? x (a) 5.75 × 106 electrons and 8.49 × 106 protons 4.39e-13 What is the charge of an electron? What is the charge of a proton? C (b) 200 electrons and 109 protons 1.60e-10 What is the charge of an electron? What is the charge of a proton? Carrow_forwardA spider begins to spin a web by first hanging from a ceiling by his fine, silk fiber. He has a mass of 0.025 kg and a charge of 3.5 μC. A second spider with a charge of 4.2 μC rests in her own web exactly 2.1 m vertically below the first spider. (a) What is the magnitude of the electric field due to the charge on the second spider at the position of the first spider? 8.57e3 N/C (b) What is the tension in the silk fiber above the first spider? 0.125 How does the electric field relate to the force? How do you calculate the net force? Narrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning





