Chapter 3, Problem 67QAP

To determine

(a)

How long after throwing the rock, it returns to its original height.

Answer to Problem 67QAP

The rock returns to its original height 4.62 s after it was thrown.

Explanation of Solution

Given:

Speed of the rock

  $v_0=25.0\text{ m/s}$

Angle of projection of the rock

  $\theta =65.0°$

Formula used:

The equation of motion for the vertical motion of the rock can be used to determine the time it would take for it to return to the height at which it was projected.

  $\Delta y=v_{0y}t+\frac{1}{2}{a}_y{t}^2$......(1)

Here, $\Delta y$ is the total vertical displacement of the rock, $v_{0y}$ is the vertical component of the rock's velocity, $a_y$ is the acceleration acting on the rock in the vertical direction and t is the time taken by the rock to make the vertical displacement of $\Delta y$.

Calculation:

The rock is projected from point O, where the origin of the chosen coordinate system rests. The x axis is drawn parallel to the ground and the + y axis points vertically upwards. The rock moves under the action of the gravitational force. The acceleration acting on the rock acts downwards and it is equal to the acceleration of free fall.

  $a_y=g=-9.80{\text{ m/s}}^2$

The rock moves upwards and reaches the point of maximum height and then descends down to point A, which is at the same height as the point O.

This is shown in the diagram below:

  

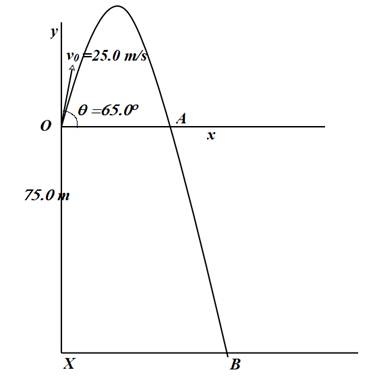
The total vertical displacement made by the rock when it reaches point A is equal to zero.

Therefore, $\Delta y=0\text{ m}$.

Calculate the vertical component of the rock's velocity.

  $\begin{array}{c}{v}_{0y}=v_0\sin \theta \\ =\left(25.0\text{ m/s}\right)\left(\sin 65.0°\right)\\ =22.66\text{ m/s}\end{array}$

Substitute 0 m for

  $\Delta y$, 22.66 m/s for $v_{0y}$ and $-9.80{\text{ m/s}}^2$ for $a_y$ in equation (1) and solve for t.

  $\begin{array}{c}\Delta y=v_{0y}t+\frac{1}{2}{a}_y{t}^2\\ 0\text{ m}=\left(22.66\text{ m/s}\right)t+\frac{1}{2}\left(-9.80{\text{ m/s}}^2\right)t^2\\ t=-\frac{2\left(22.66\text{ m/s}\right)}{\left(-9.80{\text{ m/s}}^2\right)}\\ =4.62\text{ s}\end{array}$

Conclusion:

Thus, the rock returns to its original height 4.62 s after it was thrown.

To determine

(b)

When the stone projected from the top of the dam would hit the water flowing out of the dam.

Answer to Problem 67QAP

The stone would hit the water after 6.86 s after it was thrown and the sound of splash would reach us 0.303 s later.

Explanation of Solution

Given:

Height of the dam from the ground

  $\Delta y=-75.0\text{ m}$

Speed of the rock

  $v_0=25.0\text{ m/s}$

Angle of projection of the rock

  $\theta =65.0°$

Speed of sound in air

  $v_s=344\text{ m/s}$

Formula used:

The equation for the vertical motion of the rock is

  $\Delta y=v_{0y}t+\frac{1}{2}{a}_y{t}^2$......(1)

Here,

  $\Delta y$ is the total vertical displacement of the rock,

  $v_{0y}$ is the vertical component of the rock's velocity, $a_y$ is the acceleration acting on the rock in the vertical direction and t is the time taken by the rock to make the vertical displacement of

  $\Delta y$.

The equation for the horizontal motion of the rock is

  $\Delta x=v_{0x}t+\frac{1}{2}{a}_x{t}^2$......(2)

Here, $\Delta x$ is the horizontal displacement of the rock, $v_{0x}$ is the horizontal component of the rock's velocity, $a_x$ is the acceleration along the x direction and t is the time of flight of the rock.

The time taken by sound to reach the point of projection is given by,

  $t_s=\frac{d}{v_s}$......(3)

Here, d is the total distance traveled by sound with a speed $v_s$.

Calculation:

The vertical component of the rock's velocity, calculated in part (a) is

  $v_{0y}=22.66\text{ m/s}$

The total vertical displacement made by the rock when it reaches the water is equal to the height of the dam.

In equation (1), substitute $-75.0\text{ m}$ for $\Delta y$ ( the negative sign is affixed since the height of the dam is measured downwards from the origin), 22.66 m/s for $v_{0y}$ and $-9.80{\text{ m/s}}^2$ for $a_y$ and solve for t.

  $\begin{array}{c}\Delta y=v_{0y}t+\frac{1}{2}{a}_y{t}^2\\ \left(-75.0\text{ m}\right)=\left(22.66\text{ m/s}\right)t+\frac{1}{2}\left(-9.80{\text{ m/s}}^2\right)t^2\end{array}$

Rearrange the equation.

  $\left(4.90{\text{ m/s}}^2\right)t^2-\left(22.66\text{ m/s}\right)t+\left(-75.0\text{ m}\right)=0$

Solve for t.

  $\begin{array}{c}t=\frac{-\left(-22.66\text{ m/s}\right)\pm \sqrt{{\left(-22.66\text{ m/s}\right)}^2-4\left(4.90{\text{ m/s}}^2\right)\left(-75.0\text{ m}\right)}}{2\left(4.90{\text{ m/s}}^2\right)}\\ =\frac{\left(22.66\text{ m/s}\right)\pm \left(44.54\text{ m/s}\right)}{\left(9.80{\text{ m/s}}^2\right)}\end{array}$

Taking the positive root,

  $t=6.86\text{ s}$

The stone splashes into water at point B, which is at a horizontal distance $\Delta x$ from the point vertically below the point of projection.

  

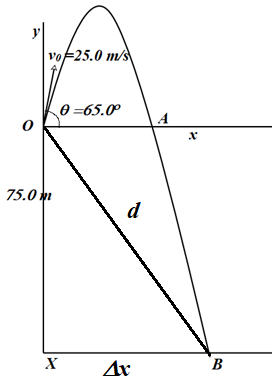
No force acts on the rock in the horizontal direction, hence the acceleration $a_x=0{\text{ m/s}}^2$.

Calculate the horizontal component of the rock's velocity.

  $\begin{array}{c}{v}_{0x}=v_0\cos \theta \\ =\left(25.0\text{ m/s}\right)\left(\cos 65.0°\right)\\ =10.56\text{ m/s}\end{array}$

Substitute 10.56 m/s for $v_{0x}$, 6.86 s for t and 0 m/s² for $a_x$ in equation (2) and determine the value of $\Delta x$.

  $\begin{array}{c}\Delta x=v_{0x}t+\frac{1}{2}{a}_x{t}^2\\ =\left(10.56\text{ m/s}\right)\left(6.86\text{ s}\right)+\frac{1}{2}\left(0{\text{ m/s}}^2\right){\left(6.86\text{ s}\right)}^2\\ =72.5\text{ m}\end{array}$

The sound of splash starts from point B and travels along BO to reach the point of projection.

Calculate the distance travelled by sound.

  $\begin{array}{c}d=\sqrt{{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2}\\ =\sqrt{{\left(72.5\text{ m}\right)}^2+{\left(-75.0\text{ m}\right)}^2}\\ =104.3\text{ m}\end{array}$

Calculate the time taken by the sound of splash to reach the point of projection using equation (3).

  $\begin{array}{c}{t}_s=\frac{d}{v_s}\\ =\frac{104.3\text{ m}}{344\text{ m/s}}\\ =0.303\text{ s}\end{array}$

Conclusion:

Thus, the stone would hit the water after 6.86 s after it was thrown and the sound of splash would reach us 0.303 s later