Videos
(a)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
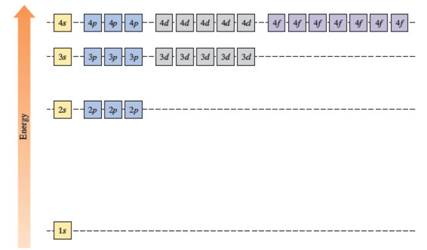
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in
To find: Identify the orbital which is higher in energy in the given pair 1s, 2s orbitals of hydrogen.
Find the value of ‘n’
(b)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 2p, 3p orbitals of hydrogen
Find the value of ‘n’
(c)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 3dxy, 3dyz orbitals of hydrogen
Find the value of ‘n’
(d)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 3s, 3d orbitals of hydrogen
Find the value of ‘n’
(e)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 4f, 5s orbitals of hydrogen
Find the value of ‘n’
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
GEN COMBO CHEMISTRY: ATOMS FIRST; ALEKS 360 2S ACCESS CARD CHEMISTRY:ATOMS FIRST
- Can you explain how I get these here and show the steps plz?arrow_forwardGive the IUPAC name for this compound Hydrocarbon Condensed Formulas Hint C2H5 CH2CH3 expand that in all the formula Part A: (CH3)2CHCH(C2H5)CH2CH2CH3 Give the IUPAC name for this compound. Part B: CH2=C(C2H5)CH2CH2CH3 Give the IUPAC name for this compound. Part C: (CH3)2C=CHC(C2H5)=CH2 Give the IUPAC name for this compound. Part D: CH3C=CCH(C2H5)2 Give the IUPAC name for this compound. Part E: (CH3)3CC=CCH2CH=C(CH3)2arrow_forwardSelect/ Match the correct letter from the image below for the IUPAC names given below: A B C D 3 E F G H K L Part 1. 4-methylheptane For example.mmmm Answer Letter H _for part 1 Part 2. 2,4-dimethylhexane Part 3. 2,3-dimethylpentane Part 4. 2,2-dimethylhexane Part 5. 2-ethyl-1,1,3,3-tetramethylcyclopentane Part 6. 3-ethyl-2-methylpentanearrow_forward
- Can u show the process as to how to get these?arrow_forwardSketch the expected 'H NMR spectra for the following compound. Label all of the H's in the structure and the corresponding signal for the spectra you sketch. Make sure you include the integration value and the splitting pattern for each signal Indicate how many signals you would expect in the 13C NMRarrow_forwardUse IUPAC naming rules to name the following hydrocarbon compounds: CH2-CH3 | a) CH-CH-CH2-CH-CH-CH3 b) | CH2 CH3 | CH3 CH3 \ / C=C H 1 H CH2-CH3 c) d) CH=C-CH3 e) CH3-CH2-CH2-CH=CH-CH3 f) CH2=CH-CH2-CH=CH-CH3 g) CH3-CH2-C = C-CH2-CH3 h)arrow_forward
- Q5 Name the following : a. b. C. d. e.arrow_forward25. Predict the major product of the following reaction. 1 equivalent of each of the starting materials was used. H₂C CH3 CH3 H3C H3C H3C. CH2 + H3C. heat CH3 CH H.C. CH3 H.C H.C CH3 CH CH3 CH3 A B C Earrow_forwardFind chemical structures based on the below information. a) Chemical formula C6H8O Compound is aromatic plus has two 1H NMR peaks that integrated for 3 each that are singlets (it could have more peaks in the 1H NMR b) Chemical Formula: C6H100 Compounds is conjugated 'H NMR has a signal that integrates for 6 and is a doublet IR spectra has a signal at 1730 cm-1arrow_forward
- Jaslev Propose a synthesis of the following starting from benzene and any other reagents and chemicals. No mechanisms are required. Indicate the condition for each step plus the major product for each step. More than two steps are required. Step 1 Step 2 مہد Brarrow_forwardPart C: The line formula for another branched alkane is shown below. i. In the IUPAC system what is the root or base name of this compound? ii. How many alkyl substituents are attached to the longest chain? iii. Give the IUPAC name for this compound.arrow_forwardPart D: Draw the Structural Formula for 4-ethyl-2-methylhexane Part E. Draw the Structural Formula for 1-chloro-3,3-diethylpentane (Chloro = Cl)arrow_forward
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning