Chapter 28, Problem 74P

(a)

To determine

Plot of wave function as a function of $x$.

Answer to Problem 74P

The wave function was plotted as a function of $x$.

Explanation of Solution

Write the given wave function of the electron.

    $\psi \left(x\right)=\{\begin{array}{l}A{e}^{-\alpha x}forx>0\\ A{e}^{+\alpha x}forx<0\end{array}$                                                                                    (I)

Here, $\psi \left(x\right)$ is the wave function, $A$ is the constant, $\alpha$ is a constant.

Write the formula to calculate the probability of finding a particle in a certain range.

    $P={\displaystyle \underset{a}{\overset{b}{\int }}\psi *\psi dx}\text{:}$                                                                                                           (II)

Here, $P$ is the probability, $\psi *$ is the complex conjugate of the wave function, $\left[a,b\right]$ is the range in which the probability is found out.

Refer equation (I) and plot the wave function as a function of $x$.

Figure 1 below shows the plot of wave function.

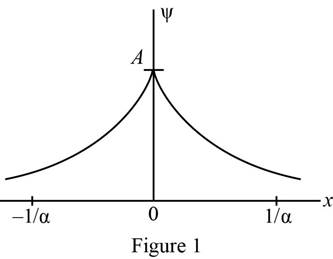
Conclusion:

The wave function was plotted as a function of $x$.

(b)

To determine

Plot of probability density as a function of $x$.

Answer to Problem 74P

The probability density was plotted as a function of $x$.

Explanation of Solution

Write the given wave function of the electron.

    $\psi \left(x\right)=\{\begin{array}{l}A{e}^{-\alpha x}forx>0\\ A{e}^{+\alpha x}forx<0\end{array}$                                                                                    (I)

Here, $\psi \left(x\right)$ is the wave function, $A$ is the constant, $\alpha$ is a constant.

Write the formula to calculate the probability of finding a particle in a certain range.

    $P={\displaystyle \underset{a}{\overset{b}{\int }}\psi *\psi dx}\text{:}$                                                                                                          (II)

Here, $P$ is the probability, $\psi *$ is the complex conjugate of the wave function, $\left[a,b\right]$ is the range in which the probability is found out.

Refer equation (II) and plot the probability density as a function of $x$.

Figure 2 below shows the plot of wave function.

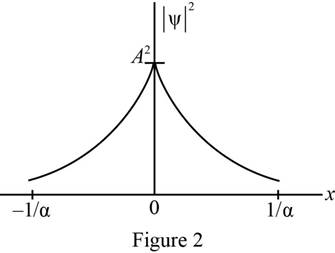
Conclusion:

The probability density was plotted as a function of $x$.

(c)

To determine

To show that $\psi \left(x\right)$ is physically reasonable wave function.

Answer to Problem 74P

The $\psi \left(x\right)$ satisfy all the conditions to be a reasonable wave function. Thus $\psi \left(x\right)$ is a physically reasonable wave function.

Explanation of Solution

Write the given wave function of the electron.

    $\psi \left(x\right)=\{\begin{array}{l}A{e}^{-\alpha x}forx>0\\ A{e}^{+\alpha x}forx<0\end{array}$                                                                                     (I)

Here, $\psi \left(x\right)$ is the wave function, $A$ is the constant, $\alpha$ is a constant.

For the wave function to be a reasonable wave function, there are set of condition.

The $\psi \left(x\right)$ has to be continuous to be a reasonable wave function. The given wave function is continuous everywhere except at infinity.

As $x\to \pm \infty$ the $\psi \left(x\right)$ must go to zero to be a reasonable wave function. The given wave function satisfy this condition.

The $\psi \left(x\right)$ can also be normalized which is an essential requirement to be a wave function.

The $\psi \left(x\right)$ satisfy all the conditions to be a reasonable wave function. Thus $\psi \left(x\right)$ is a physically reasonable wave function.

Conclusion:

The $\psi \left(x\right)$ satisfy all the conditions to be a reasonable wave function. Thus $\psi \left(x\right)$ is a physically reasonable wave function.

(d)

To determine

To normalize the wave function.

Answer to Problem 74P

The normalization constant of the given wave function is $\sqrt{\alpha }$.

Explanation of Solution

Write the given wave function of the electron.

    $\psi \left(x\right)=\{\begin{array}{l}A{e}^{-\alpha x}forx>0\\ A{e}^{+\alpha x}forx<0\end{array}$                                                                                     (I)

Here, $\psi \left(x\right)$ is the wave function, $A$ is the constant, $\alpha$ is a constant.

Write the condition for normalized wave function.

    ${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|\psi \right|}^{2}dx}=1$

The wave function is symmetric. Thus re-write the above condition.

    $2{\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|\psi \right|}^{2}dx}=1$

Substitute equation (I) in the above equation.

    $\begin{array}{c}2A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-2\alpha x}dx}=1\\ \left(\frac{2A^2}{-2\alpha }\right)\left(e^{-\infty }-e^0\right)=1\\ \frac{2A^2}{2\alpha }=1\\ A=\sqrt{\alpha }\end{array}$

Conclusion:

The normalization constant of the given wave function is $\sqrt{\alpha }$.

(e)

To determine

The probability of finding the electron in the range $-\frac{1}{2\alpha }\le x\le \frac{1}{2\alpha }$.

Answer to Problem 74P

The probability of finding the particle in the range $-\frac{1}{2\alpha }\le x\le \frac{1}{2\alpha }$ is $0.632$.

Explanation of Solution

Refer section (d) and write the given normalized wave function of the electron.

    $\psi \left(x\right)=\{\begin{array}{l}\sqrt{\alpha }{e}^{-\alpha x}forx>0\\ \sqrt{\alpha }{e}^{+\alpha x}forx<0\end{array}$                                                                                  (II)

Here, $\psi \left(x\right)$ is the wave function, and $\alpha$ is a constant.

Write the formula to calculate the probability of finding a particle in a certain range.

    $P={\displaystyle \underset{a}{\overset{b}{\int }}{\left|\psi \right|}^{2}dx}\text{:}$                                                                                                      (III)

Here, $P$ is the probability, and $\left[a,b\right]$ is the range in which the probability is found out.

Refer equation (II) in equation (III) to determine probability in range $-\frac{1}{2\alpha }\le x\le \frac{1}{2\alpha }$.

    $\begin{array}{c}P={\left(\sqrt{a}\right)}^2{\displaystyle \underset{-1/2\alpha }{\overset{1/2\alpha }{\int }}{e}^{-2\alpha x}dx}\\ =2{\left(\sqrt{a}\right)}^2{\displaystyle \underset{x=0}{\overset{1/2\alpha }{\int }}{e}^{-2\alpha x}dx}\\ =\left(\frac{2\alpha }{-2\alpha }\right)\left(e^{-2\alpha /2\alpha }-1\right)\\ =\left(1-e^{-1}\right)\\ =0.632\end{array}$

Conclusion:

The probability of finding the particle in the range $-\frac{1}{2\alpha }\le x\le \frac{1}{2\alpha }$ is $0.632$.