Chapter 28, Problem 27P

The basic differential equation of the elastic curve for a uniformly loaded beam (Fig. P28.27) is given as

$EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$

Where $E=\text{the}$ modulus of elasticity and $I=\text{the}$ moment of inertia. Solve for the deflection of the beam using (a) the finite difference approach $\left(\Delta x=2\text{ft}\right)$ and (b) the shooting method. The following parameter values apply: $E=30,000\text{ksi}$, $I=800{\text{in}}^4,w=1\text{kip/ft, }L=10\text{ft}$ Compare your numerical results to the analytical solution,

$y=\frac{wL{x}^3}{12EI}-\frac{w{x}^4}{24EI}-\frac{w{L}^{3}x}{24EI}$

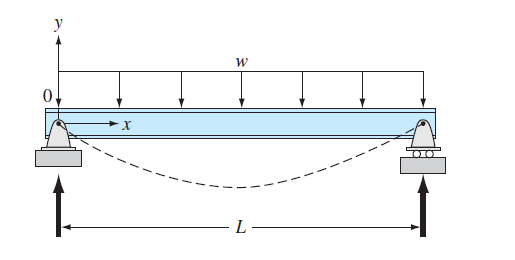
FIGURE P28.27

To determine

To calculate: The deflection of the beam by the finite-difference method with $\Delta x=2\text{ ft}$ if the differential equation for the elastic curve for a uniformly loaded beam is given as $EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$. Also, compare the result with the analytical solution.

Answer to Problem 27P

Solution:

The deflection of the beam by the finite-difference method is,

x	y	y-Analytical
0	0	0
24	$-0.00576$	$-0.00557$
48	$-0.009216$	$-0.00892$
72	$-0.009216$	$-0.00892$
96	$-0.00576$	$-0.00557$
120	0	0

Explanation of Solution

Given Information:

The differential equation for the elastic curve for a uniformly loaded beam is given as,

$EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$

Formula to find analytical value,

$y=\frac{wL{x}^3}{12EI}-\frac{w{x}^4}{24EI}-\frac{w{L}^{3}x}{24EI}$

Where,

The modulus of elasticity, $E=30,000\text{ ksi}$.

The moment of inertia, $I=800{\text{ in}}^4$.

The values,

$\begin{array}{l}w=1\text{ kip/ft}\\ L=10\text{ ft}\end{array}$

Formula used:

The conversion formula,

$1\text{ ft}=12\text{ in}$

The value of second order derivative by finite difference method is given as,

$\frac{d^{2}T}{d{x}^2}=\frac{T_{i+1}-2T_i+T_{i-1}}{\Delta x^2}$

Calculation:

Consider the equation,

$EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$

Rewrite the above equation as,

$\frac{d^{2}y}{d{x}^2}=\frac{wx}{2EI}\left(L-x\right)$

Substitute the values, $E=30,000\text{ ksi, }I=800{\text{ in}}^4,w=0.0833\text{ kip/in and }L=120\text{ in}$ in the above equation,

$\begin{array}{c}\frac{d^{2}y}{d{x}^2}=\frac{0.0833x}{2\times 30000\times 800}\left(120-x\right)\\ =1.735\times {10}^{-9}x\left(120-x\right)\\ =208.2\times {10}^{-9}x-1.735\times {10}^{-9}{x}^2\end{array}$

Now, the second order derivative by finite difference method gives,

$\frac{d^{2}y}{d{x}^2}=\frac{y_{i+1}-2y_i+y_{i-1}}{{\left(\Delta x\right)}^2}$

Therefore,

$\begin{array}{c}\frac{y_{i+1}-2y_i+y_{i-1}}{{\left(24\right)}^2}=208.2\times {10}^{-9}{x}_i-1.735\times {10}^{-9}{x}_i{}^2\\ y_{i+1}-2y_i+y_{i-1}=576\left(208.2\times {10}^{-9}{x}_i-1.735\times {10}^{-9}{x}_i{}^2\right)\\ y_{i+1}-2y_i+y_{i-1}=1.2\times {10}^{-4}{x}_i-1\times {10}^{-6}{x}_i{}^2\end{array}$

Put $i=1$ for the first node,

$\begin{array}{c}{y}_{1+1}-2y_1+y_{1-1}=1.2\times {10}^{-4}{x}_1-1\times {10}^{-6}{x}_1{}^2\\ y_2-2y_1+y_0=1.2\times {10}^{-4}{x}_1-1\times {10}^{-6}{x}_1{}^2\end{array}$

The boundary condition is, $y_0=0$ and $x_1=24$.Thus,

$\begin{array}{c}{y}_2-2y_1+0=1.2\times {10}^{-4}\left(24\right)-1\times {10}^{-6}{\left(24\right)}^2\\ y_2-2y_1=2.304\times {10}^{-3}\end{array}$

Put $i=2$ for the second node,

$\begin{array}{c}{y}_{2+1}-2y_2+y_{2-1}=1.2\times {10}^{-4}{x}_2-1\times {10}^{-6}{x}_2{}^2\\ y_3-2y_2+y_1=1.2\times {10}^{-4}{x}_2-1\times {10}^{-6}{x}_2{}^2\end{array}$

Substitute $x_2=48$ in the above equation,

$\begin{array}{c}{y}_3-2y_2+y_1=1.2\times {10}^{-4}\times 48-1\times {10}^{-6}\times {\left(48\right)}^2\\ =57.6\times {10}^{-4}-2304\times {10}^{-6}\\ =3.456\times {10}^{-3}\end{array}$

Put $i=3$ for the third node,

$\begin{array}{c}{y}_{3+1}-2y_3+y_{3-1}=1.2\times {10}^{-4}{x}_3-1\times {10}^{-6}{x}_3{}^2\\ y_4-2y_3+y_2=1.2\times {10}^{-4}{x}_3-1\times {10}^{-6}{x}_3{}^2\end{array}$

Substitute $x_2=72$ in the above equation,

$\begin{array}{c}{y}_4-2y_3+y_2=1.2\times {10}^{-4}\times 72-1\times {10}^{-6}\times {\left(72\right)}^2\\ =3.456\times {10}^{-3}\end{array}$

Put $i=4$ for the fourth node,

$\begin{array}{c}{y}_{4+1}-2y_4+y_{4-1}=1.2\times {10}^{-4}{x}_4-1\times {10}^{-6}{x}_4{}^2\\ y_5-2y_4+y_3=1.2\times {10}^{-4}{x}_4-1\times {10}^{-6}{x}_4{}^2\end{array}$

Substitute $x_2=96$ and the boundary condition $y_5=0$ in the above equation,

$\begin{array}{c}{y}_5-2y_4+y_3=1.2\times {10}^{-4}\times 96-1\times {10}^{-6}\times {\left(96\right)}^2\\ -2y_4+y_3=2.304\times {10}^{-3}\end{array}$

The matrix form of the above equations is given as below,

$\left[\begin{array}{cccc}-2& 1& 0& 0\\ 1& -2& 1& 0\\ 0& 1& -2& 1\\ 0& 0& 1& -2\end{array}\right]\left\{\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\end{array}\right\}=\left\{\begin{array}{c}2.304\times {10}^{-3}\\ 3.456\times {10}^{-3}\\ 3.456\times {10}^{-3}\\ 2.304\times {10}^{-3}\end{array}\right\}$

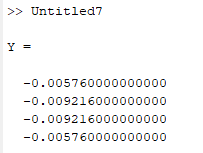
Use MATLAB to find the solution of the above system as below,

Code:

%Write the matrix

A=[-2 1 0 0; 1 -2 1 0; 0 1 -2 1; 0 0 1 -2];

%write the values of rhs

b=[0.002304 0.003456 0.003456 0.002304]';

%find the result

Y=A\b

Output:

Now, for the analytical value, consider the equation $y=\frac{wL{x}^3}{12EI}-\frac{w{x}^4}{24EI}-\frac{w{L}^{3}x}{24EI}$.

Substitute the values, $E=30,000\text{ ksi, }I=800{\text{ in}}^4,w=0.0833\text{ kip/in and }L=120\text{ in}$ in the above equation,

$\begin{array}{c}y=\frac{0.0833x}{12\times 30000\times 800}\left(120x^2-\frac{x^3}{2}-\frac{{\left(120\right)}^3}{2}\right)\\ =2.89236\times {10}^{-10}x\left(120x^2-0.5x^3-864000\right)\end{array}$

Use excel to find the values of y at different values of x as below,

Step 1: Name the column A as x and go to column A2 and put 0 then go to column A3 and write the formula as,

=A2+24

Then, Press enter and drag the column up to $x=120$.

Step 2: Now name the column B as y and go to column B2 andwrite the formula as,

=2.89236*10^(-10)*A2*(120*A2^2-0.5*A2^3-864000)

Step 3: Press enter and drag the column up to $x=120$.

The result obtained as,

x	y-Analytical
0	0
24	$-0.00557$
48	$-0.00892$
72	$-0.00892$
96	$-0.00557$
120	0

To determine

To calculate: The deflection of the beam by the shooting method with $\Delta x=2\text{ ft}$ if the differential equation for the elastic curve for a uniformly loaded beam is given as $EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$. Also, compare the result with the analytical solution.

Answer to Problem 27P

Solution:

A few values of deflection of the beam by the shooting method is,

x	y	z
0	0	-1.6E-06
0.25	-4.1E-07	-1.6E-06
0.5	-8.2E-07	-1.6E-06
0.75	-1.2E-06	-1.6E-06
1	-1.6E-06	-1.6E-06
1.25	-2E-06	-1.5E-06
1.5	-2.4E-06	-1.4E-06
1.75	-2.8E-06	-1.4E-06
2	-3.2E-06	-1.3E-06
2.25	-3.5E-06	-1.2E-06
2.5	-3.8E-06	-1.1E-06
2.75	-4.1E-06	-1E-06
3	-4.4E-06	-9E-07

Explanation of Solution

Given Information:

The differential equation for the elastic curve for a uniformly loaded beam is given as,

$EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$

Formula to find analytical value,

$y=\frac{wL{x}^3}{12EI}-\frac{w{x}^4}{24EI}-\frac{w{L}^{3}x}{24EI}$

Where,

The modulus of elasticity, $E=30,000\text{ ksi}$.

The moment of inertia, $I=800{\text{ in}}^4$.

The values,

$\begin{array}{l}w=1\text{ kip/ft}\\ L=10\text{ ft}\end{array}$

Formula used:

The conversion formula,

$1\text{ ft}=12\text{ in}$

Calculation:

Consider the equation,

$EI\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2}-\frac{w{x}^2}{2}$

Rewrite the equation as,

$\frac{d^{2}y}{d{x}^2}=\frac{wLx}{2EI}-\frac{w{x}^2}{2EI}$

Assume $\frac{dy}{dx}=z$. Thus,

$\begin{array}{c}\frac{dz}{dx}=\frac{wLx}{2EI}-\frac{w{x}^2}{2EI}\\ =\frac{w}{2EI}\left(Lx-x^2\right)\end{array}$

Substitute the values, $E=30,000\text{ ksi, }I=800{\text{ in}}^4,w=0.0833\text{ kip/in and }L=120\text{ in}$ in the above equation,

$\begin{array}{c}\frac{dz}{dx}=\frac{0.0833\times 120x}{2\times 30000\times 800}-\frac{0.0833x^2}{2\times 30000\times 800}\\ =1.73542\times {10}^{-9}\left(120x-x^2\right)\end{array}$

Use VBA program as below to solve the above differential equation as below,

Code:

OptionExplicit

'Create a function find

Subfind()

'declare the variables as integer

Dim n AsInteger, j AsInteger

'declare the variables as double

DimdydxAsDouble, x AsDouble, dy2dx AsDouble, yanalAsDouble, E AsDouble, I AsDouble, w AsDouble, L AsDouble

DimolddydxAsDouble, oldy AsDouble, y AsDouble, h AsDouble

'Set the values of the variables

E =30000

I =800

w =1

L =10

y =0

x =0

h =0.25

dydx=0

'store dydx and analytical solution

dydx= caldydx(w, E, I, L, x)

yanal= caly(w, E, I, L, x)

'use for loop to determine different value of y and y analytical

For j =1 To41

'store the value of y at oldy and dydx in olddydx

oldy = y

olddydx= dydx

'Store d2ydx, dydx and analytical solution

dy2dx = caldy2dx(w, E, I, L, x)

dydx= caldydx(w, E, I, L, x)

yanal= caly(w, E, I, L, x)

'move to the cell b3

Range("b1"). Select

ActiveCell.Value="shooting method"

'Assign name to the columns

ActiveCell.Offset(1,0). Select

ActiveCell.Value="x"

ActiveCell.Offset(0,1). Select

ActiveCell.Value="y"

ActiveCell.Offset(0,1). Select

ActiveCell.Value="z"

ActiveCell.Offset(0,1). Select

ActiveCell.Value="dy2dx"

ActiveCell.Offset(0,1). Select

ActiveCell.Value="y-anal"

'dislay values in cell

Range("b2"). Select

ActiveCell.Offset(j,0). Select

ActiveCell.Value= x

ActiveCell.Offset(0,1). Select

ActiveCell.Value= oldy

ActiveCell.Offset(0,1). Select

ActiveCell.Value= dydx

ActiveCell.Offset(0,1). Select

ActiveCell.Value= dy2dx

ActiveCell.Offset(0,1). Select

ActiveCell.Value= yanal

'Write the next value of x

x = x + h

'Write the next value of y by euler method

y = oldy + olddydx* h

Next

EndSub

'Define d2ydx function

Function caldy2dx(w, E, I, L, x)

'Declare the variables

Dim t AsDouble

'Write the formula

t =((w * L * x)/(2* E * I))-((w * x * x)/(2* E * I))

'Store the value

caldy2dx = t

EndFunction

'Define dydx

Functioncaldydx(w, E, I, L, x)

'Declare the variables

Dim t AsDouble, c AsDouble

'Set the values

c =-0.000001648

'Write the formula

t =((w * L * x * x)/(4* E * I))-((w * x * x * x)/(6* E * I))+ c

'Store the value

caldydx= t

EndFunction

'Define the function caly for analytical value

Functioncaly(w, E, I, L, x)

'Declare the variables

Dim t AsDouble

'Write the formula

t =((w * L * x * x * x)/(12* E * I))-((w * x * x * x * x)/(24* E * I))-((w * L * L * L * x)/(24* E * I))

'Store the value

caly= t

EndFunction

Output:

shooting method
x	y	z	dy2dx	y-anal
0	0	-1.6E-06	0	0
0.25	-4.1E-07	-1.6E-06	5.08E-08	-4.3E-07
0.5	-8.2E-07	-1.6E-06	9.9E-08	-8.6E-07
0.75	-1.2E-06	-1.6E-06	1.45E-07	-1.3E-06
1	-1.6E-06	-1.6E-06	1.88E-07	-1.7E-06
1.25	-2E-06	-1.5E-06	2.28E-07	-2.1E-06
1.5	-2.4E-06	-1.4E-06	2.66E-07	-2.5E-06
1.75	-2.8E-06	-1.4E-06	3.01E-07	-2.9E-06
2	-3.2E-06	-1.3E-06	3.33E-07	-3.2E-06
2.25	-3.5E-06	-1.2E-06	3.63E-07	-3.6E-06
2.5	-3.8E-06	-1.1E-06	3.91E-07	-3.9E-06
2.75	-4.1E-06	-1E-06	4.15E-07	-4.2E-06
3	-4.4E-06	-9E-07	4.38E-07	-4.4E-06
3.25	-4.7E-06	-7.9E-07	4.57E-07	-4.6E-06
3.5	-4.9E-06	-6.7E-07	4.74E-07	-4.8E-06
3.75	-5.1E-06	-5.5E-07	4.88E-07	-5E-06
4	-5.2E-06	-4.3E-07	5E-07	-5.2E-06
4.25	-5.4E-06	-3E-07	5.09E-07	-5.3E-06
4.5	-5.5E-06	-1.7E-07	5.16E-07	-5.4E-06
4.75	-5.6E-06	-4.2E-08	5.2E-07	-5.4E-06
5	-5.6E-06	8.81E-08	5.21E-07	-5.4E-06
5.25	-5.6E-06	2.18E-07	5.2E-07	-5.4E-06
5.5	-5.6E-06	3.48E-07	5.16E-07	-5.4E-06
5.75	-5.5E-06	4.76E-07	5.09E-07	-5.3E-06
6	-5.4E-06	6.02E-07	5E-07	-5.2E-06
6.25	-5.3E-06	7.26E-07	4.88E-07	-5E-06
6.5	-5.2E-06	8.46E-07	4.74E-07	-4.8E-06
6.75	-5E-06	9.62E-07	4.57E-07	-4.6E-06
7	-4.8E-06	1.07E-06	4.38E-07	-4.4E-06
7.25	-4.5E-06	1.18E-06	4.15E-07	-4.2E-06
7.5	-4.3E-06	1.28E-06	3.91E-07	-3.9E-06
7.75	-4E-06	1.38E-06	3.63E-07	-3.6E-06
8	-3.7E-06	1.46E-06	3.33E-07	-3.2E-06
8.25	-3.3E-06	1.54E-06	3.01E-07	-2.9E-06
8.5	-3E-06	1.61E-06	2.66E-07	-2.5E-06
8.75	-2.6E-06	1.68E-06	2.28E-07	-2.1E-06
9	-2.2E-06	1.73E-06	1.88E-07	-1.7E-06
9.25	-1.7E-06	1.77E-06	1.45E-07	-1.3E-06
9.5	-1.3E-06	1.8E-06	9.9E-08	-8.6E-07
9.75	-8.7E-07	1.82E-06	5.08E-08	-4.3E-07
10	-4.2E-07	1.82E-06	0	0

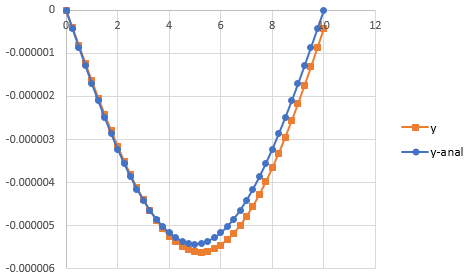
Now, to draw the graph of y and y-analytical follow the step as below,

Step 1: Select the cell from B2 to B43 and cell C2 to C43. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 2: Select the cell from B2 to B43 and cell F2 to F43. Then, go to the Insert and select the scatter with smooth lines from the chart.

Step 3: Select one of the graphs and paste it on another graph to merge the graphs.

The graph obtained is,