
(a)
A spreadsheet for
(a)
Answer to Problem 80AP
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
Explanation of Solution
Given information: Th first symbol i.e. Euler’s number is
It is given that the expression for the current-voltage characteristic curve for a semiconductor diode as a function of temperature
Here,
Formula to calculate the resistance across the diode is,
Here,
The value of magnitude of electron charge is
The value of Boltzmann’s constant is
The value of voltage across the diode varies from
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
Conclusion:
Therefore, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
(b)
To draw: The graph for
(b)
Answer to Problem 80AP
The graph for
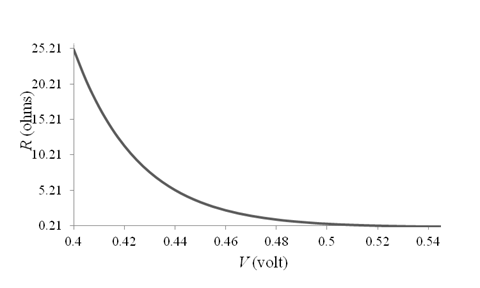
The graph for
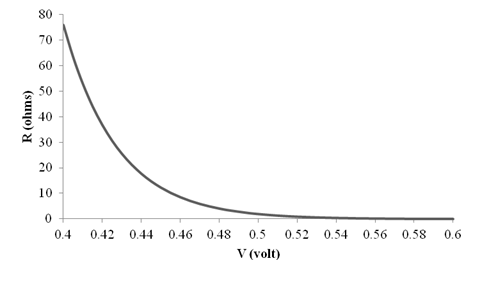
The graph for
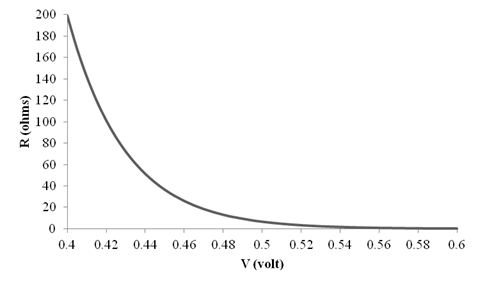
Explanation of Solution
Given information: The first symbol i.e. Euler’s number is
The different values of the
Thus, the graph for
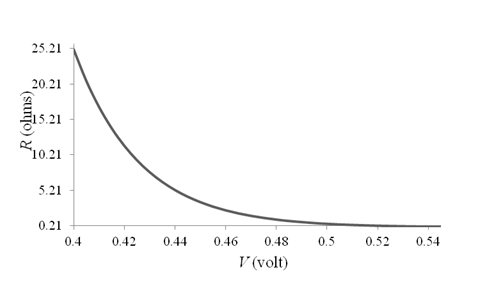
The different values of the
Thus, the graph for
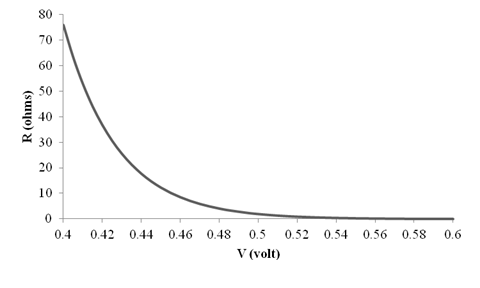
The different values of the
The graph for
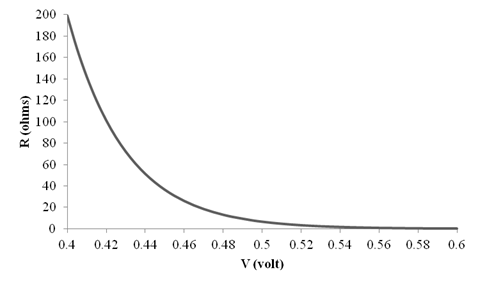
Conclusion:
Therefore, the graph for

Therefore, the graph for

Therefore, the graph for
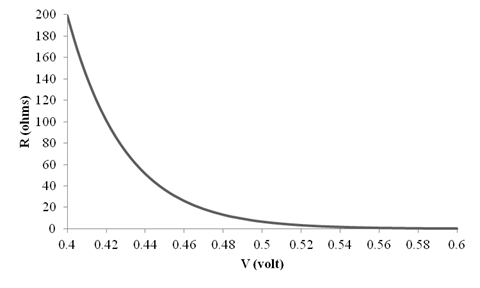
Want to see more full solutions like this?
Chapter 27 Solutions
Physics for Scientists and Engineers with Modern, Revised Hybrid (with Enhanced WebAssign Printed Access Card for Physics, Multi-Term Courses)
- What are the expected readings of the ammeter and voltmeter for the circuit in the figure below? (R = 5.60 Ω, ΔV = 6.30 V) ammeter I =arrow_forwardsimple diagram to illustrate the setup for each law- coulombs law and biot savart lawarrow_forwardA circular coil with 100 turns and a radius of 0.05 m is placed in a magnetic field that changes at auniform rate from 0.2 T to 0.8 T in 0.1 seconds. The plane of the coil is perpendicular to the field.• Calculate the induced electric field in the coil.• Calculate the current density in the coil given its conductivity σ.arrow_forward
- An L-C circuit has an inductance of 0.410 H and a capacitance of 0.250 nF . During the current oscillations, the maximum current in the inductor is 1.80 A . What is the maximum energy Emax stored in the capacitor at any time during the current oscillations? How many times per second does the capacitor contain the amount of energy found in part A? Please show all steps.arrow_forwardA long, straight wire carries a current of 10 A along what we’ll define to the be x-axis. A square loopin the x-y plane with side length 0.1 m is placed near the wire such that its closest side is parallel tothe wire and 0.05 m away.• Calculate the magnetic flux through the loop using Ampere’s law.arrow_forwardDescribe the motion of a charged particle entering a uniform magnetic field at an angle to the fieldlines. Include a diagram showing the velocity vector, magnetic field lines, and the path of the particle.arrow_forward
- Discuss the differences between the Biot-Savart law and Coulomb’s law in terms of their applicationsand the physical quantities they describe.arrow_forwardExplain why Ampere’s law can be used to find the magnetic field inside a solenoid but not outside.arrow_forward3. An Atwood machine consists of two masses, mA and m B, which are connected by an inelastic cord of negligible mass that passes over a pulley. If the pulley has radius RO and moment of inertia I about its axle, determine the acceleration of the masses mA and m B, and compare to the situation where the moment of inertia of the pulley is ignored. Ignore friction at the axle O. Use angular momentum and torque in this solutionarrow_forward
- A 0.850-m-long metal bar is pulled to the right at a steady 5.0 m/s perpendicular to a uniform, 0.650-T magnetic field. The bar rides on parallel metal rails connected through a 25-Ω, resistor (Figure 1), so the apparatus makes a complete circuit. Ignore the resistance of the bar and the rails. Please explain how to find the direction of the induced current.arrow_forwardFor each of the actions depicted, determine the direction (right, left, or zero) of the current induced to flow through the resistor in the circuit containing the secondary coil. The coils are wrapped around a plastic core. Immediately after the switch is closed, as shown in the figure, (Figure 1) in which direction does the current flow through the resistor? If the switch is then opened, as shown in the figure, in which direction does the current flow through the resistor? I have the answers to the question, but would like to understand the logic behind the answers. Please show steps.arrow_forwardWhen violet light of wavelength 415 nm falls on a single slit, it creates a central diffraction peak that is 8.60 cm wide on a screen that is 2.80 m away. Part A How wide is the slit? ΟΙ ΑΣΦ ? D= 2.7.10-8 Submit Previous Answers Request Answer × Incorrect; Try Again; 8 attempts remaining marrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





