Chapter 27, Problem 10P

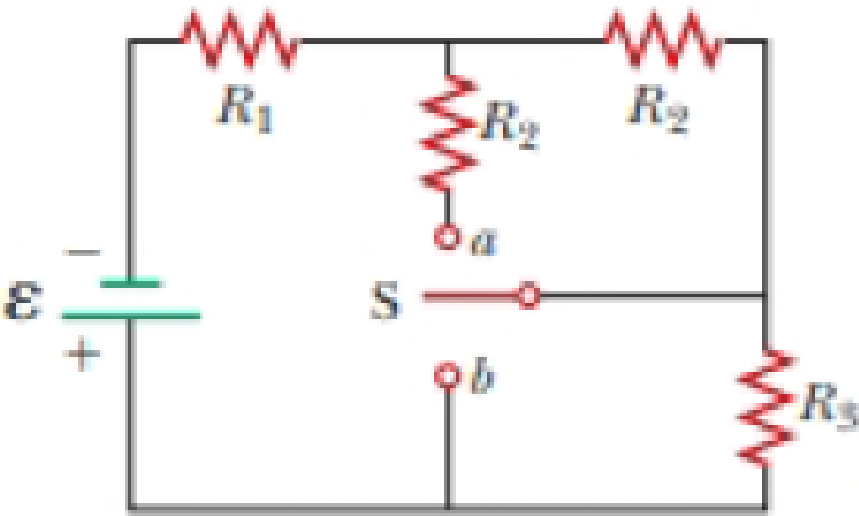
A battery with emf ε and no internal resistance supplies current to the circuit shown in Figure P27.9. When the double-throw switch S is open as shown in the figure, the current in the battery is I₀. When the switch is closed in position a, the current in the battery is I_a. When the switch is closed in position b, the current in the battery is I_b. Find the resistances (a) R₁, (b) R₂, and (c) R₃.

Figure P27.9 Problems 9 and 10.

To determine

The expression of the resistance $R_1$.

Answer to Problem 10P

The expression of the resistance $R_1$ is $2\epsilon \left(\frac{1}{I_a}-\frac{1}{I_0}+\frac{1}{2I_b}\right)\Omega$.

Explanation of Solution

Given information: Emf across the battery is $\epsilon$, current in the battery when the switch S is open is $I_0$, current in the battery when the switch is closed in position $a$ is $I_a$, current in the battery when the switch is closed in position $b$ is $I_b$.

When the switch S is open, then the three resistors $R_1,R_2\text{and}{R}_3$ are in series.

Formula to calculate the equivalent resistance across the circuit, when the switch S is open.

$\begin{array}{c}V=I_0{R}_{\text{eq1}}\\ R_{\text{eq1}}=\frac{V}{I_0}\end{array}$ (1)

Here,

$R_{\text{eq1}}$ is the equivalent resistance across the circuit, when the switch S is open.

$V$ is the voltage across the battery.

$I_0$ is the current in the battery when the switch S is open.

As the total emf across the battery is equal to the voltage across the battery.

$\epsilon =V$

Here,

$\epsilon$ is the total emf across the battery.

Substitute $\epsilon$ for $V$ in equation (1) to find $R_{\text{eq1}}$,

$R_{\text{eq1}}=\frac{\epsilon }{I_0}$ (2)

Formula to calculate the equivalent resistance across the circuit, when the switch S is open.

$R_{\text{eq1}}=R_1+R_2+R_3$ (3)

Here,

$R_1$ is the value of resistance 1.

$R_2$ is the value of resistance 2.

$R_3$ is the value of resistance 3.

Substitute $\frac{\epsilon }{I_0}$ for $R_{\text{eq1}}$ in equation (3),

$R_1+R_2+R_3=\frac{\epsilon }{I_0}$ (4)

When the switch is closed in position $a$, then the three resistors $R_1,R_P\text{and}{R}_3$ are in series.

From equation (2), formula to calculate the equivalent resistance across the circuit, when the switch is closed in position $a$,

$R_{\text{eq2}}=\frac{\epsilon }{I_a}$ (5)

Here,

$R_{\text{eq2}}$ is the equivalent resistance across the circuit, when the switch is closed in position $a$.

$I_a$ is the current in the battery when the switch is closed in position $a$.

Formula to calculate the resistance when the resistors are connected in parallel.

$R_P=\frac{R_2{R}_2}{R_2+R_2}$

From equation (3), formula to calculate the equivalent resistance across the circuit, when the switch is closed in position $a$.

$R_{\text{eq2}}=R_1+R_P+R_3$ (6)

Substitute $\frac{R_2{R}_2}{R_2+R_2}$ for $R_P$ in equation (6),

$R_{\text{eq2}}=R_1+\frac{R_2{R}_2}{R_2+R_2}+R_3$ (7)

Substitute $\frac{\epsilon }{I_a}$ for $R_{\text{eq2}}$ in equation (7),

$\begin{array}{c}{R}_1+\frac{R_2{R}_2}{R_2+R_2}+R_3=\frac{\epsilon }{I_a}\\ R_1+\frac{R_2}{2}+R_3=\frac{\epsilon }{I_a}\end{array}$ (8)

When the switch is closed in position $b$, then the $R_3$ resistor is short circuited and the two resistors $R_1\text{and}{R}_2$ are in series.

From equation (2), formula to calculate the equivalent resistance across the circuit, when the switch is closed in position $b$,

$R_{\text{eq3}}=\frac{\epsilon }{I_b}$ (9)

Here,

$R_{\text{eq3}}$ is the equivalent resistance across the circuit, when the switch is closed in position $b$.

$I_b$ is the current in the battery when the switch is closed in position $a$.

From equation (3), formula to calculate the equivalent resistance across the circuit, when the switch is closed in position $b$.

$R_{\text{eq3}}=R_1+R_2$ (10)

Substitute $\frac{\epsilon }{I_b}$ for $R_{\text{eq3}}$ in equation (10),

$R_1+R_2=\frac{\epsilon }{I_b}$ (11)

Subtract equation (11) from (4) to find $R_3$,

$\begin{array}{c}{R}_1+R_2+R_3-\left(R_1+R_2\right)=\frac{\epsilon }{I_0}-\frac{\epsilon }{I_b}\\ R_3=\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega \end{array}$ (12)

Thus, the expression of the resistance $R_3$ is $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$.

Subtract equation (11) from (8) to find $R_2$,

$\begin{array}{c}{R}_1+\frac{R_2}{2}+R_3-\left(R_1+R_2\right)=\frac{\epsilon }{I_a}-\frac{\epsilon }{I_b}\\ R_3-\frac{R_2}{2}=\epsilon \left(\frac{1}{I_a}-\frac{1}{I_b}\right)\Omega \end{array}$ (13)

Substitute $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$ for $R_{\text{3}}$ in equation (13) to find $R_2$,

$\begin{array}{c}\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega -\frac{R_2}{2}=\epsilon \left(\frac{1}{I_a}-\frac{1}{I_b}\right)\Omega \\ \frac{R_2}{2}=\epsilon \left(\frac{1}{I_a}-\frac{1}{I_0}\right)\Omega \\ R_2=2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega \end{array}$ (14)

Thus, the expression of the resistance $R_2$ is $2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega$.

Substitute $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$ for $R_{\text{3}}$, $2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega$ for $R_2$ in equation (4) to find $R_1$,

$\begin{array}{c}{R}_1+2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega +\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega =\frac{\epsilon }{I_0}\\ R_1=\frac{\epsilon }{I_0}-2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega -\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega \\ R_1=2\epsilon \left(\frac{1}{I_a}-\frac{1}{I_0}+\frac{1}{2I_b}\right)\Omega \end{array}$

Thus, the expression of the resistance $R_1$ is $2\epsilon \left(\frac{1}{I_a}-\frac{1}{I_0}+\frac{1}{2I_b}\right)\Omega$.

Conclusion:

Therefore, the expression of the resistance $R_1$ is $2\epsilon \left(\frac{1}{I_a}-\frac{1}{I_0}+\frac{1}{2I_b}\right)\Omega$.

To determine

The expression of the resistance $R_2$.

Answer to Problem 10P

The expression of the resistance $R_2$ is $2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega$.

Explanation of Solution

Given information: Emf across the battery is $\epsilon$, current in the battery when the switch S is open is $I_0$, current in the battery when the switch is closed in position $a$ is $I_a$, current in the battery when the switch is closed in position $b$ is $I_b$.

From part (a) equation (17), the expression for the resistance $R_2$ is $2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega$.

Thus, the expression of the resistance $R_2$ is $2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega$.

Conclusion:

Therefore, the expression of the resistance $R_2$ is $2\epsilon \left(\frac{1}{I_0}-\frac{1}{I_a}\right)\Omega$.

To determine

The expression of the resistance $R_3$.

Answer to Problem 10P

The expression of the resistance $R_3$ is $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$.

Explanation of Solution

Given information: Emf across the battery is $\epsilon$, current in the battery when the switch S is open is $I_0$, current in the battery when the switch is closed in position $a$ is $I_a$, current in the battery when the switch is closed in position $b$ is $I_b$.

From part (a) equation (15), the expression for the resistance $R_3$ is $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$

Thus, the expression of the resistance $R_3$ is $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$.

Conclusion:

Therefore, the expression of the resistance $R_3$ is $\epsilon \left(\frac{1}{I_0}-\frac{1}{I_b}\right)\Omega$.