Chapter 2.6, Problem 36E

Solution

The match of the functions, $f\left(x\right)=3-\frac{2}{x-1}$ with given graphs.

The graph of $f\left(x\right)=3-\frac{2}{x-1}$ is (c).

Given:

The graphs are given as follows,

  

  

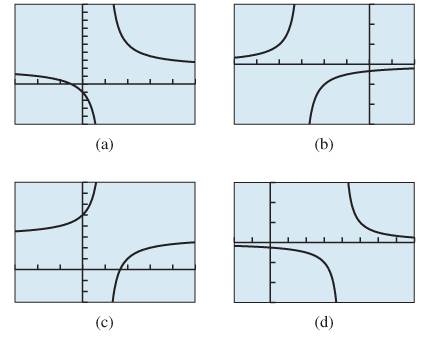
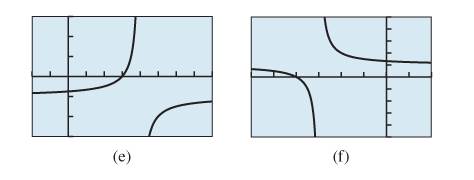
Concept Used:

The graph of a function of type $f\left(x\right)=\frac{ax+b}{cx+d}$ where $c\ne 0$ can be obtained by using the transformation of basic reciprocal function $\frac{1}{x}$ .

The graph of basic reciprocal function $f\left(x\right)=\frac{1}{x}$ is given by,

  

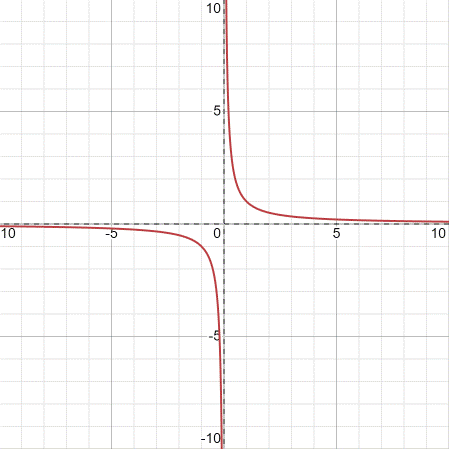
Here, horizontal asymptotes is $x=0$ , vertical asymptotes is, $y=0$ and $\underset{x\to {\infty }^{-}}{\lim }f\left(x\right)=\underset{x\to {\infty }^{+}}{\lim }f\left(x\right)=0$ .

The transformation in $f\left(x\right)$ is as follows,

1) The graph of $-f\left(x\right)$ is the reflection in y -axis of $f\left(x\right)$ .

2) The graph of $a\cdot f\left(x\right)$ is the vertical stretch of $f\left(x\right)$ by scale factor a parallel to y -axis.

3) By translation property, the of graph $a+f\left(x\right)$ is the vertical translation of $f\left(x\right)$ by a units up or down according a is positive or negative respectively.

4) The graph of $f\left(x-a\right)$ is horizontal translation of $f\left(x\right)$ by a units right.

Calculation:

Consider the function, $f\left(x\right)=3-\frac{2}{x-1}$ .

If the basic reciprocal function is $g\left(x\right)=\frac{1}{x}$ , then $f\left(x\right)=3-2g\left(x-1\right)$ is reflection in y -axis, then vertical stretch by scale factor two parallel to y- axis and the vertical translation by three units up and horizontal translation by one units right.

The graph of $f\left(x\right)=3-\frac{2}{x-1}$ is as follows,

  

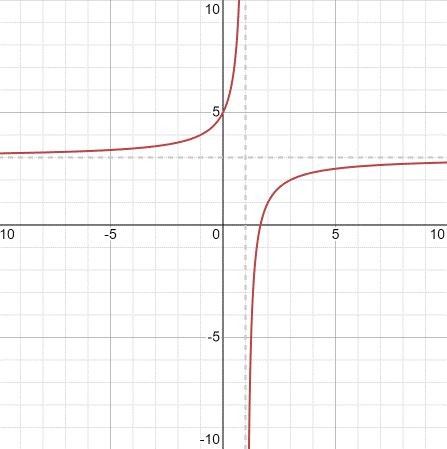
Hence, from the given graphs, the graph of $f\left(x\right)=3-\frac{2}{x-1}$ is (c).

Conclusion:

The graph of $f\left(x\right)=3-\frac{2}{x-1}$ is (c).