
Concept explainers
The asymptotes and intercepts of function and graph the function.
The vertical asymptotes is
Given:
The function is
Concept Used:
If a polynomial function in the form
And,
The end behaviour asymptote given by
The condition can be concluded as,
1) If
2) If
3) If
And,
The x -intercept is given by zeros of numerator that are not zero of denominator. And y -intercept is given by
From using asymptotes and intercepts the graph can be drawn.
Calculation:
Consider the function,
To find vertical asymptotes, find the zeros of denominator, so factorize the denominator
Thus, the zeros of denominator of
To find end behaviour asymptotes, find
Since,
Now find the intercept, the x -intercept is given by zeros of numerator that are not zero of denominator. Hence solve
The x -intercept are
And y -intercept is given by
Thus y -intercept is
Hence, using vertical asymptotes
the graph obtain is as:
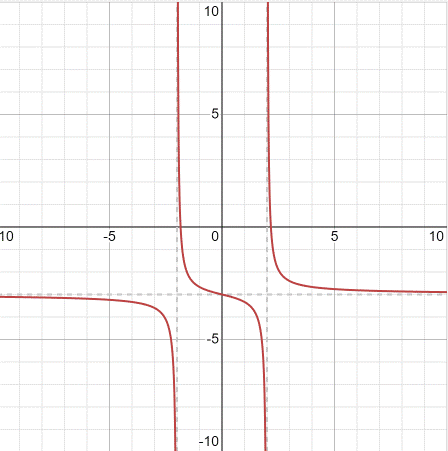
Conclusion:
The vertical asymptotes is
Chapter 2 Solutions
Precalculus: Graphical, Numerical, Algebraic Common Core 10th Edition
- 3.17 (B). A simply supported beam has a span of 6 m and carries a distributed load which varies in a linea manner from 30 kN/m at one support to 90 kN/m at the other support. Locate the point of maximum bendin moment and calculate the value of this maximum. Sketch the S.F. and B.M. diagrams. [U.L.] [3.25 m from l.h. end; 272 KN m 30. 90arrow_forward3.11 (B). A beam, 12 m long, is to be simply supported at 2m from each end and to carry a U.d.l of 30kN/m together with a 30 KN point load at the right-hand end. For ease of transportation the beam is to be jointed in two places, one joint being Situated 5 m from the left-hand end. What load (to the nearest KN) must be applied to the left-hand end to ensure that there is no B.M. at the joint (i.e. the joint is to be a point of contraflexure)? What will then be the best position on the beam for the other joint? Determine the position and magnitude of the maximum B.M. present on the beam. [114 KN, 1.6 m from r.h. reaction; 4.7 m from 1.h. reaction; 43.35 KN m.]arrow_forward2. Using vector algebraic operations, if - Ả = 2ây – mây – C - B = mây tây – 2, C = ây + mây + 20, D = m x + mây tậ Z Find the value(s) of m such that (a) Ả is perpendicular to B (b) B is parallel to Carrow_forward
- 1. Determine whether the following sets are subspaces of $\mathbb{R}^3$ under the operations of addition and scalar multiplication defined on $\mathbb{R}^3$. Justify your answers.(a) $W_1=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1=3 a_2\right.$ and $\left.a_3=\mid a_2\right\}$(b) $W_2=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1=a_3+2\right\}$(c) $W_3=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: 2 a_1-7 a_2+a_3=0\right\}$(d) $W_4=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1-4 a_2-a_3=0\right\}$(e) $W_s=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1+2 a_2-3 a_3=1\right\}$(f) $W_6=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: 5 a_1^2-3 a_2^2+6 a_3^2=0\right\}$arrow_forward3 Evaluate the double integral 10 y√x dy dx. First sketch the area of the integral involved, then carry out the integral in both ways, first over x and next over y, and vice versa.arrow_forwardQuestion 2. i. Suppose that the random variable X takes two possible values 1 and -1, and P(X = 1) = P(X-1)=1/2. Let Y=-X. Are X and Y the same random variable? Do X and Y have the same distribution? Explain your answer. ii. Suppose that the random variable X~N(0, 1), let Y=-X. Are X and Y the same random variable? Do X and Y have the same distribution? Explain your answer.arrow_forward
- Problem 4. Let f(x, y) = { Find P(X <1/2|Y = 1/2). c(x + y²) 0arrow_forwardQize f(x) x + 2x2 - 2 x² + 4x² - 4 Solve the equation using Newton Raphsonarrow_forwardSolve please thanks!arrow_forwardSolve please and thank youarrow_forwardAccording to Newton's law of universal gravitation, the force F between two bodies of constant mass GmM m and M is given by the formula F = , where G is the gravitational constant and d is the d² distance between the bodies. a. Suppose that G, m, and M are constants. Find the rate of change of force F with respect to distance d. F' (d) 2GmM b. Find the rate of change of force F with gravitational constant G = 6.67 × 10-¹¹ Nm²/kg², on two bodies 5 meters apart, each with a mass of 250 kilograms. Answer in scientific notation, rounding to 2 decimal places. -6.67x10 N/m syntax incomplete.arrow_forwardSolve please and thank youarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





