
a.
To Find: The derivatives of
a.
Answer to Problem 50E
Its limit is
Explanation of Solution
Given:
With the grapher in degree mode, graph
Compare the estimation with
Find the reason if any to believe the limit should be
Graph of
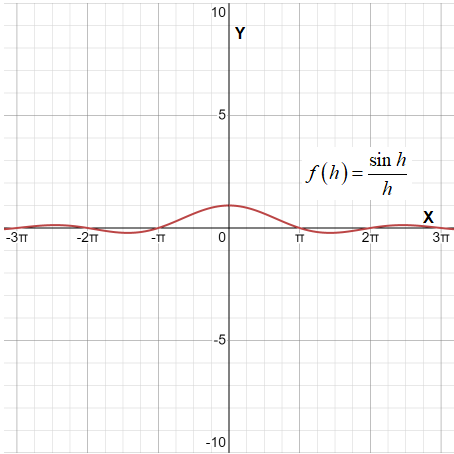
The value of
The value of
To Convert degrees to radians and vice versa:
Thus, the limit can be:
b.
To Estimate: The given function by setting the grapher in degree mode.
b.
Answer to Problem 50E
The value of the function
Explanation of Solution
Given:
With the grapher in degree mode, graph
Graph of the function
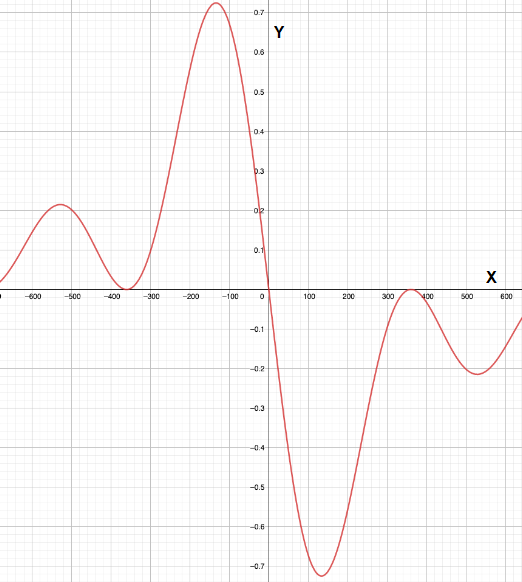
It can be seen from the graph, that the limit as
Thus,
c.
To Find: The formula that obtained for the derivative.
c.
Answer to Problem 50E
The formula that obtained for the derivative is
Explanation of Solution
Given:
Go back to the derivation of the formula for the derivative of
Considering the derivative:
Using the formula:
Apply limit to all the function:
Hence,
d.
To Derive: The formula for the derivative of
d.
Answer to Problem 50E
The formula for the derivative of
Explanation of Solution
Given:
Derive the formula for the derivative of
Given that,
Using the formula:
Here
Substituting the values into the formula:
Apply limit to all the function:
Hence,
e.
To Derive: The second and third degree-mode derivatives of
Explain the disadvantages of the degree-mode formulas become even more apparent
when taking derivatives of higher order.
e.
Answer to Problem 50E
The second order derivative of
The third order derivative of
The second order derivative of
The third order derivative of
Explanation of Solution
Given:
Derive the second and third degree-mode derivatives of
Given that the second and third order derivative of
The second order derivative of
The third order derivative of
Likewise, the second order derivative of
The third order derivative of
Chapter 2 Solutions
CALCULUS-W/XL ACCESS
- Find the equation of the line / in the figure below. Give exact values using the form y = mx + b. m = b = y WebAssign Plot f(x) = 10* log 9 Xarrow_forwardA particle travels along a straight line path given by s=9.5t3-2.2t2-4.5t+9.9 (in meters). What time does it change direction? Report the higher of the answers to the nearest 2 decimal places in seconds.arrow_forwardUse the method of disks to find the volume of the solid that is obtained when the region under the curve y = over the interval [4,17] is rotated about the x-axis.arrow_forward
- 1. Find the area of the region enclosed between the curves y = x and y = x. Sketch the region.arrow_forwardfor the given rectangular coordinates, find two sets of polar coordinates for which 0≤θ<2π, one with r>0 and the other with r<0. (-2sqrt(3),9)arrow_forwardI circled the correct answer, could you show me how to do it using divergence and polar coordinatesarrow_forward
- The correct answer is D Could you explain and show the steps pleasearrow_forwardTaylor Series Approximation Example- H.W More terms used implies better approximation f(x) 4 f(x) Zero order f(x + 1) = f(x;) First order f(x; + 1) = f(x;) + f'(x;)h 1.0 Second order 0.5 True f(x + 1) = f(x) + f'(x)h + ƒ"(x;) h2 2! f(x+1) 0 x; = 0 x+1 = 1 x h f(x)=0.1x4-0.15x³- 0.5x2 -0.25x + 1.2 51 Taylor Series Approximation H.w: Smaller step size implies smaller error Errors f(x) + f(x,) Zero order f(x,+ 1) = f(x) First order 1.0 0.5 Reduced step size Second order True f(x + 1) = f(x) + f'(x)h f(x; + 1) = f(x) + f'(x)h + "(xi) h2 f(x,+1) O x₁ = 0 x+1=1 Using Taylor Series Expansion estimate f(1.35) with x0 =0.75 with 5 iterations (or & s= 5%) for f(x)=0.1x 0.15x³-0.5x²- 0.25x + 1.2 52arrow_forwardCould you explain this using the formula I attached and polar coorindatesarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





