
a.
To Describe: The motion of the particle for
a.
Answer to Problem 37E
In the beginning, the particle was moving in a positive direction until
Explanation of Solution
Given:
The position
And
Using the power rule, the derivative of
This derivative will represent velocity:
Find the velocity when it equal to
As the particle will have zero velocity at maximum or minimum, this will tell us the time when the particle reached its maximum/minimum.
Use the quadratic formula:
Therefore, until approximately
Once the particle's velocity was
From that point on, the particle again changed direction and moved in a positive direction.
b.
To Describe: The time, in which the particle speeds up and slows down.
b.
Answer to Problem 37E
At the intervals
At the intervals
Explanation of Solution
Given:
The position
Given the equation:
When velocity and acceleration have the same sign (both positive or both negative), a particle is speeding up, while a particle is slowing down when the signs are opposite (one is positive and the other is negative).
From part a) The velocity is positive when
Find the second derivative of
Set the above equation equal to
Test the value between 0 and
So, Take
Test the value greater than
So, take
Hence, the acceleration is positive when
At the interval,
At the interval,
At the interval,
Both acceleration and velocity are positive for
So,
At the intervals
At the intervals
c.
To Find: The time the particle changing its direction.
c.
Answer to Problem 37E
The particle changing its direction at
Explanation of Solution
Given:
The position
The equation:
When the particle velocity is
As mentioned in part
d.
To Find: The time at which the particle is at rest.
d.
Answer to Problem 37E
At
Explanation of Solution
Given:
The position
The equation:
When the particle velocity is
From part
So, at
e.
To Describe: The velocity and the speed of the particle.
e.
Answer to Problem 37E
Velocity:
Initially, the velocity was positive, but it stopped increasing, and then it became negative, and then it increased again, and then it became positive again then continue to increase.
Speed:
During the first part of the equation, the speed drops to zero at
Explanation of Solution
Given:
The position
The equation:
State the velocity and the speed of the particle:
It's calculates from part
Hence at the time at
There is a positive velocity at first since,
At
Thereafter, it will increase to infinity again.
Due to the initial decrease in velocity, the speed will also decrease until
It then increases until
Diagrammatic representation is as follows:
The graph of
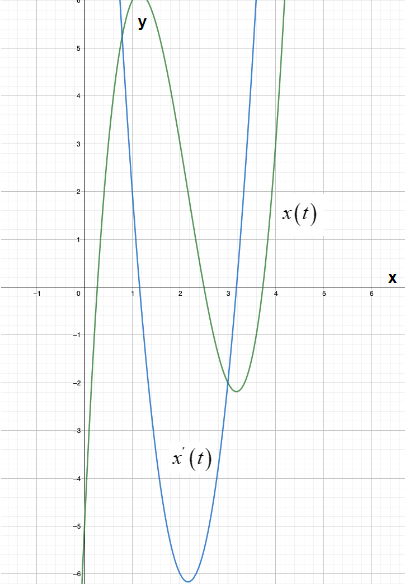
e.
To Describe: The time in which the particle at the point
e.
Answer to Problem 37E
The time in which the particle at the point
Explanation of Solution
Given:
The position
Given the equation:
Find the time, the particle is at
Position of the particle at time
So, set
Subtract
Find the value of
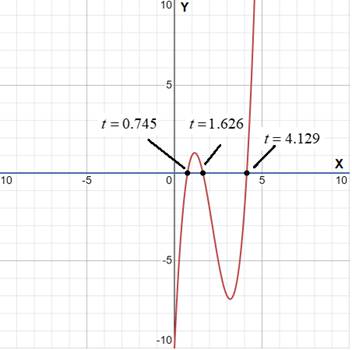
Thus, the values of
Chapter 2 Solutions
CALCULUS-W/XL ACCESS
- 12. [0/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.022. Evaluate the indefinite integral. (Use C for the constant of integration.) sin(In 33x) dxarrow_forward2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.003.MI. Evaluate the integral by making the given substitution. (Use C for the constant of integration.) x³ + 3 dx, u = x² + 3 Need Help? Read It Watch It Master It SUBMIT ANSWER 3. [-/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.006.MI. Evaluate the integral by making the given substitution. (Use C for the constant of integration.) | +8 sec² (1/x³) dx, u = 1/x7 Need Help? Read It Master It SUBMIT ANSWER 4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.007.MI. Evaluate the indefinite integral. (Use C for the constant of integration.) √x27 sin(x28) dxarrow_forward53,85÷1,5=arrow_forward
- 3. In the space below, describe in what ways the function f(x) = -2√x - 3 has been transformed from the basic function √x. The graph f(x) on the coordinate plane at right. (4 points) -4 -&- -3 -- -2 4 3- 2 1- 1 0 1 2 -N -1- -2- -3- -4- 3 ++ 4arrow_forward2. Suppose the graph below left is the function f(x). In the space below, describe what transformations are occuring in the transformed function 3ƒ(-2x) + 1. The graph it on the coordinate plane below right. (4 points)arrow_forward1 1. Suppose we have the function f(x) = = and then we transform it by moving it four units to the right and six units down, reflecting it horizontally, and stretching vertically by 5 units. What will the formula of our new function g(x) be? (2 points) g(x) =arrow_forward
- Suppose an oil spill covers a circular area and the radius, r, increases according to the graph shown below where t represents the number of minutes since the spill was first observed. Radius (feet) 80 70 60 50 40 30 20 10 0 r 0 10 20 30 40 50 60 70 80 90 Time (minutes) (a) How large is the circular area of the spill 30 minutes after it was first observed? Give your answer in terms of π. square feet (b) If the cost to clean the oil spill is proportional to the square of the diameter of the spill, express the cost, C, as a function of the radius of the spill, r. Use a lower case k as the proportionality constant. C(r) = (c) Which of the following expressions could be used to represent the amount of time it took for the radius of the spill to increase from 20 feet to 60 feet? r(60) - r(20) Or¹(80-30) r(80) - r(30) r-1(80) - r−1(30) r-1(60) - r¹(20)arrow_forward6. Graph the function f(x)=log3x. Label three points on the graph (one should be the intercept) with corresponding ordered pairs and label the asymptote with its equation. Write the domain and range of the function in interval notation. Make your graph big enough to see all important features.arrow_forwardFind the average value gave of the function g on the given interval. gave = g(x) = 8√√x, [8,64] Need Help? Read It Watch Itarrow_forward
- 3. Mary needs to choose between two investments: One pays 5% compounded annually, and the other pays 4.9% compounded monthly. If she plans to invest $22,000 for 3 years, which investment should she choose? How much extra interest will she earn by making the better choice? For all word problems, your solution must be presented in a sentence in the context of the problem.arrow_forward4 πT14 Sin (X) 3 Sin(2x) e dx 1716 S (sinx + cosx) dxarrow_forwardLet g(x) = f(t) dt, where f is the function whose graph is shown. 3 y f(t) MA t (a) At what values of x do the local maximum and minimum values of g occur? Xmin = Xmin = Xmax = Xmax = (smaller x-value) (larger x-value) (smaller x-value) (larger x-value) (b) Where does g attain its absolute maximum value? x = (c) On what interval is g concave downward? (Enter your answer using interval notation.)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





