
Concept explainers
(a)
The horizontal and vertical component of electric field at a point
(a)
Answer to Problem 42P
The horizontal component of electric field at a distance
Explanation of Solution
Write the expression for the electric field at a distance
Here,
Write the value for the Coulomb’s constant.
The following figure represents the components of an electric field at a point
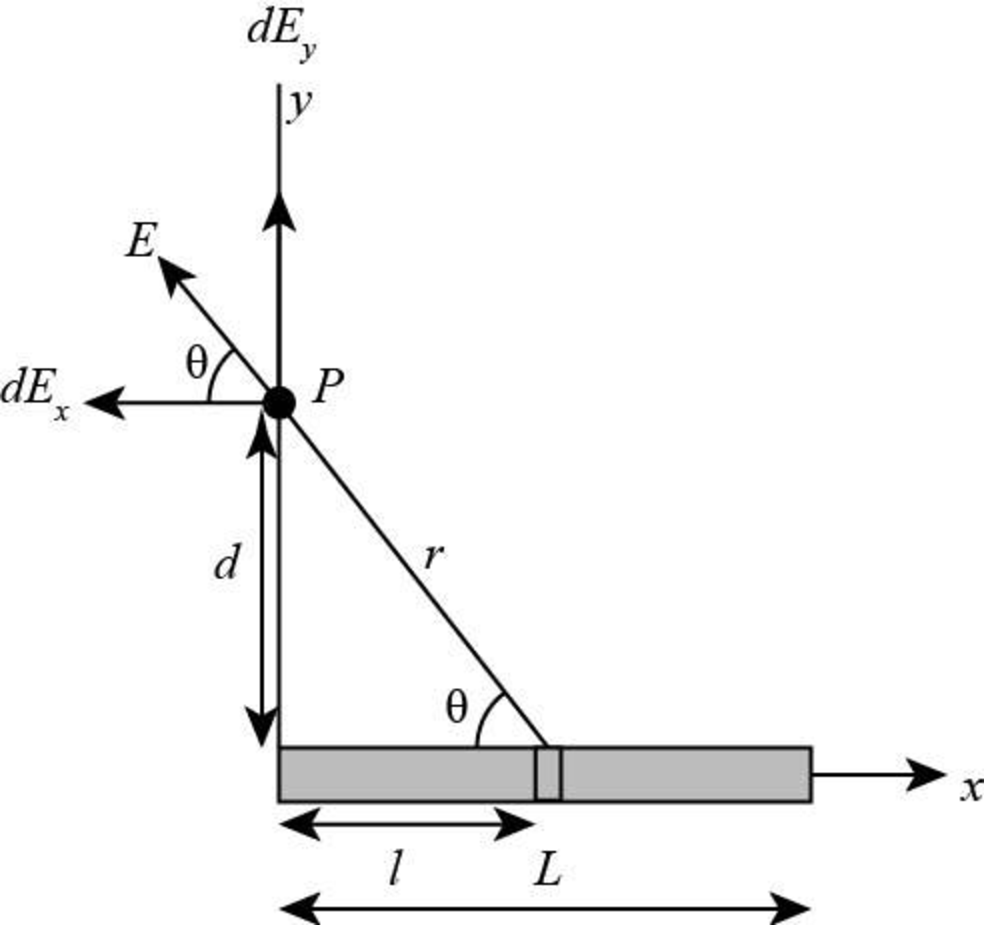
Figure-(1)
Write the expression for uniformly distributed charge along the length of the rod.
Here,
Write the expression for the charge on a small elemental length of the rod.
Here,
Write the sine expression for the right angled triangle.
Substitute
Write the cosine expression for the right angled triangle.
Substitute
Write the expression for the horizontal component of the electric field at a distance
Integrating the above equation between the limits
Write the expression for the vertical component of electric field at a distance
Integrating the above equation between the limits
Calculate the horizontal component of electric field at a distance
Substitute
Write the Pythagoras theorem to calculate the value of
Taking the cube of both sides in the above equation.
Substitute
As per the formula
Substitute
Calculate the vertical component of electric field at a distance
Substitute
Substitute
As per the formula
Substitute
Therefore, the horizontal and vertical component of electric field at a distance
(b)
The approximate values of the horizontal and vertical components, when
(b)
Answer to Problem 42P
The horizontal and vertical component of electric field at a distance
Explanation of Solution
The length of the rod
The horizontal component of the electric field in equation (IV) becomes,
The vertical component of the electric field in equation (VI) becomes,
Therefore, the horizontal and vertical component of electric field at a distance
Want to see more full solutions like this?
Chapter 23 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
- A Geiger-Mueller tube is a radiation detector that consists of a closed, hollow, metal cylinder (the cathode) of inner radius ra and a coaxial cylindrical wire (the anode) of radius г (see figure below) with a gas filling the space between the electrodes. Assume that the internal diameter of a Geiger-Mueller tube is 3.00 cm and that the wire along the axis has a diameter of 0.190 mm. The dielectric strength of the gas between the central wire and the cylinder is 1.15 × 106 V/m. Use the equation 2πrlE = 9in to calculate the maximum potential difference that can be applied between the wire and the cylinder before breakdown occurs in the gas. V Anode Cathodearrow_forward3.77 is not the correct answer!arrow_forwardA I squar frame has sides that measure 2.45m when it is at rest. What is the area of the frame when it moves parellel to one of its diagonal with a m² speed of 0.86.c as indicated in the figure? >V.arrow_forward
- An astronent travels to a distant star with a speed of 0.44C relative to Earth. From the austronaut's point of view, the star is 420 ly from Earth. On the return trip, the astronent travels speed of 0.76c relative to Earth. What is the distance covered on the return trip, as measured by the astronant? your answer in light-years. with a Give ly.arrow_forwardstar by spaceship Sixus is about 9.00 ly from Earth. To preach the star in 15.04 (ship time), how fast must you travel? C.arrow_forwardIf light-bulb A is unscrewed, how will the brightness of bulbs B and C change, if at all? How does the current drawn by from the battery change?arrow_forward
- Can someone help mearrow_forwardCan someone help me with this thank youarrow_forward(a) For a spherical capacitor with inner radius a and outer radius b, we have the following for the capacitance. ab C = k₂(b- a) 0.0695 m 0.145 m (8.99 × 10º N · m²/c²)( [0.145 m- 0.0695 m × 10-11 F = PF IIarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





