Chapter 2.2, Problem 44E

Ogive: Using the data in Exercise 28:

1. Compute the cumulative frequencies for the classes in the American League frequency distribution.
2. Construct a frequency ogive for the American League frequency distribution.
3. Compute the cumulative relative frequencies for the classes in the American League frequency distribution.
4. Construct a relative frequency ogive for the American League, using the same classes.
5. Compute the cumulative frequencies for the classes in the National League frequency distribution.
6. Construct a frequency ogive for the National League frequency distribution.
7. Compute the cumulative relative frequencies for the classes in the National League frequency distribution.
8. Construct a relative frequency ogive for the National League, using the same classes.

To determine

To compute:The cumulative frequencies for the classes in the American League frequency distribution.

Answer to Problem 44E

Batting average	American League Cumulative Frequency
0.180-0.199	2
0.200-0.219	9
0.220-0.239	30
0.240-0.259	60
0.260-0.279	86
0.280-0.299	107
0.300-0.319	119
0.320-0.339	124
0.340-0.359	124

Explanation of Solution

Given information:The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used: The cumulative frequency of a class is the sum of the frequencies of that class and all previous classes.

Calculation:

The cumulative classes are given by in the following table.

Batting average	American LeagueFrequency	American League Cumulative Frequency
0.180-0.199	2	2
0.200-0.219	7	$2+7=9$
0.220-0.239	21	$21+9=30$
0.240-0.259	30	$30+30=60$
0.260-0.279	26	$26+60=86$
0.280-0.299	21	$21+86=107$
0.300-0.319	12	$12+107=119$
0.320-0.339	5	$5+119=124$
0.340-0.359	0	$124+0=124$

Hence, the cumulative frequency for American league is given by

Batting average	American League Cumulative Frequency
0.180-0.199	2
0.200-0.219	9
0.220-0.239	30
0.240-0.259	60
0.260-0.279	86
0.280-0.299	107
0.300-0.319	119
0.320-0.339	124
0.340-0.359	124

To determine

To find:The frequency ogive for the frequency distribution.

Explanation of Solution

Given information:The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used:An ogive plots the cumulative frequencies.

Solution:

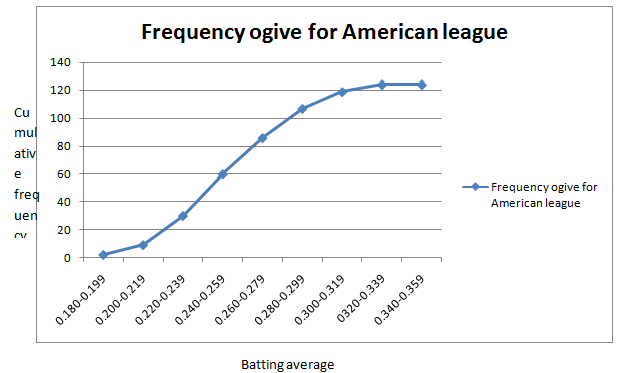
The table of cumulative American League frequency is given by

Batting average	American League Cumulative Frequency
0.180-0.199	2
0.200-0.219	9
0.220-0.239	30
0.240-0.259	60
0.260-0.279	86
0.280-0.299	107
0.300-0.319	119
0.320-0.339	124
0.340-0.359	124

The frequency ogivefor American League frequency distribution is given by

  

To determine

To compute: The cumulative relative frequencies for the classes in the American league frequency distribution.

Answer to Problem 44E

Batting average	Cumulative relative Frequency
0.180-0.199	0.016
0.200-0.219	0.073
0.220-0.239	0.242
0.240-0.259	0.484
0.260-0.279	0.694
0.280-0.299	0.863
0.300-0.319	0.960
0.320-0.339	1.000
0.340-0.359	1.000

Explanation of Solution

Given information: The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used: The cumulative relative frequency of a class is given by

  $cumulativerelativefrequency=\frac{cumulativefrequency}{Sumofallfrequency}$

Calculation:

The cumulative classes are given by in the following table.

Batting average	American League Cumulative Frequency	American League relative Cumulative Frequency
0.180-0.199	2	$\frac{2}{124}=0.016$
0.200-0.219	9	$\frac{9}{124}=0.073$
0.220-0.239	30	$\frac{30}{124}=0.242$
0.240-0.259	60	$\frac{60}{124}=0.484$
0.260-0.279	86	$\frac{86}{124}=0.694$
0.280-0.299	107	$\frac{107}{124}=0.863$
0.300-0.319	119	$\frac{119}{124}=0.960$
0.320-0.339	124	$\frac{124}{124}=1.000$
0.340-0.359	124	$\frac{124}{124}=1.000$

Hence, the cumulative relative frequency is given by

Batting average	Cumulative relative Frequency
0.180-0.199	0.016
0.200-0.219	0.073
0.220-0.239	0.242
0.240-0.259	0.484
0.260-0.279	0.694
0.280-0.299	0.863
0.300-0.319	0.960
0.320-0.339	1.000
0.340-0.359	1.000

To determine

To find: The relative frequency ogive for the American league frequency distribution.

Explanation of Solution

Given information:The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used:A relative frequency ogive plots the cumulative relative frequencies..

Solution:

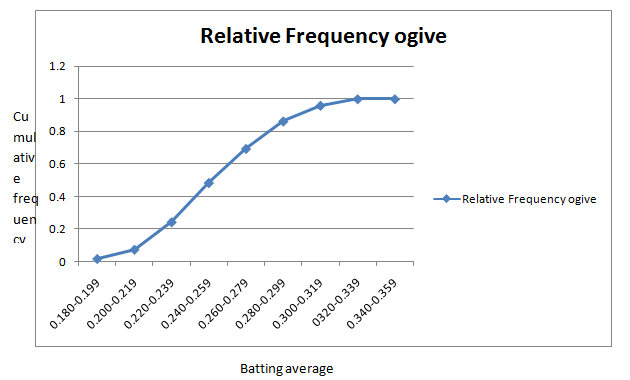
The table of cumulative relative frequency is given by

Batting average	Cumulative relative Frequency
0.180-0.199	0.016
0.200-0.219	0.073
0.220-0.239	0.242
0.240-0.259	0.484
0.260-0.279	0.694
0.280-0.299	0.863
0.300-0.319	0.960
0.320-0.339	1.000
0.340-0.359	1.000

The relative frequency ogive is given by

  

To determine

To compute: The cumulative frequencies for the classes in the National League frequency distribution.

Answer to Problem 44E

Batting average	National League Cumulative Frequency
0.180-0.199	2
0.200-0.219	9
0.220-0.239	29
0.240-0.259	58
0.260-0.279	90
0.280-0.299	120
0.300-0.319	137
0.320-0.339	142
0.340-0.359	143

Explanation of Solution

Given information: The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used: The cumulative frequency of a class is the sum of the frequencies of that class and all previous classes.

Calculation:

The cumulative classes are given by in the following table.

Batting average	National LeagueFrequency	National League Cumulative Frequency
0.180-0.199	2	2
0.200-0.219	7	$2+7=9$
0.220-0.239	20	$20+9=29$
0.240-0.259	29	$29+29=58$
0.260-0.279	32	$32+58=90$
0.280-0.299	30	$30+90=120$
0.300-0.319	17	$17+120=137$
0.320-0.339	5	$5+137=142$
0.340-0.359	1	$1+142=143$

Hence, the cumulative frequency for National league is given by

Batting average	National League Cumulative Frequency
0.180-0.199	2
0.200-0.219	9
0.220-0.239	29
0.240-0.259	58
0.260-0.279	90
0.280-0.299	120
0.300-0.319	137
0.320-0.339	142
0.340-0.359	143

To determine

To find: The frequency ogive for the National League frequency distribution.

Explanation of Solution

Given information:The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used: An ogive plots the cumulative frequencies.

Solution:

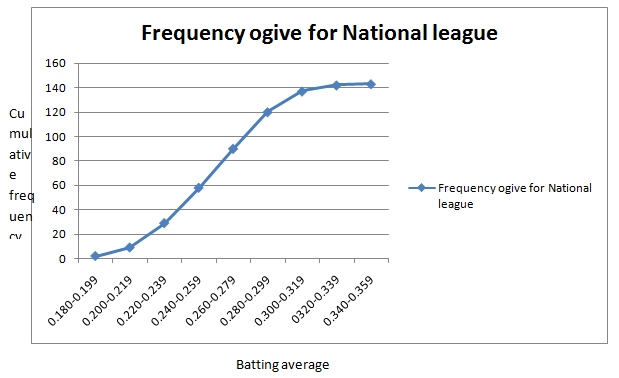
The table of cumulative National League frequency is given by

Batting average	National League Cumulative Frequency
0.180-0.199	2
0.200-0.219	9
0.220-0.239	29
0.240-0.259	58
0.260-0.279	90
0.280-0.299	120
0.300-0.319	137
0.320-0.339	142
0.340-0.359	143

The frequency ogive for National League frequency distribution is given by

  

To determine

To compute: The cumulative relative frequencies for the classes in the National league frequency distribution.

Answer to Problem 44E

Batting average	Cumulative relative Frequency
0.180-0.199	0.014
0.200-0.219	0.063
0.220-0.239	0.203
0.240-0.259	0.406
0.260-0.279	0.629
0.280-0.299	0.839
0.300-0.319	0.958
0.320-0.339	0.993
0.340-0.359	1.000

Explanation of Solution

Given information: The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used: The cumulative relative frequency of a class is given by

  $cumulativerelativefrequency=\frac{cumulativefrequency}{Sumofallfrequency}$

Calculation:

The cumulative classes are given by in the following table.

Batting average	National League Cumulative Frequency	Cumulative relative frequency
0.180-0.199	2	$\frac{2}{143}=0.014$
0.200-0.219	9	$\frac{9}{143}=0.063$
0.220-0.239	29	$\frac{29}{143}=0.203$
0.240-0.259	58	$\frac{58}{143}=0.406$
0.260-0.279	90	$\frac{90}{143}=0.629$
0.280-0.299	120	$\frac{120}{143}=0.839$
0.300-0.319	137	$\frac{137}{143}=0.958$
0.320-0.339	142	$\frac{142}{143}=0.993$
0.340-0.359	143	$\frac{143}{143}=1.000$

Hence, the cumulative relative frequency for National league is given by

Batting average	Cumulative relative Frequency
0.180-0.199	0.014
0.200-0.219	0.063
0.220-0.239	0.203
0.240-0.259	0.406
0.260-0.279	0.629
0.280-0.299	0.839
0.300-0.319	0.958
0.320-0.339	0.993
0.340-0.359	1.000

To determine

To find: The relative frequency ogive for the National league frequency distribution.

Explanation of Solution

Given information:The following frequency distribution presents the batting averages of Major League Baseball players in both the American League and the National League who had 300 or more plate appearances during a recent season.

Batting average	American LeagueFrequency	National LeagueFrequency
0.180-0.199	2	2
0.200-0.219	7	7
0.220-0.239	21	20
0.240-0.259	30	29
0.260-0.279	26	32
0.280-0.299	21	30
0.300-0.319	12	17
0.320-0.339	5	5
0.340-0.359	0	1

Definition used:A relative frequency ogive plots the cumulative relative frequencies..

Solution:

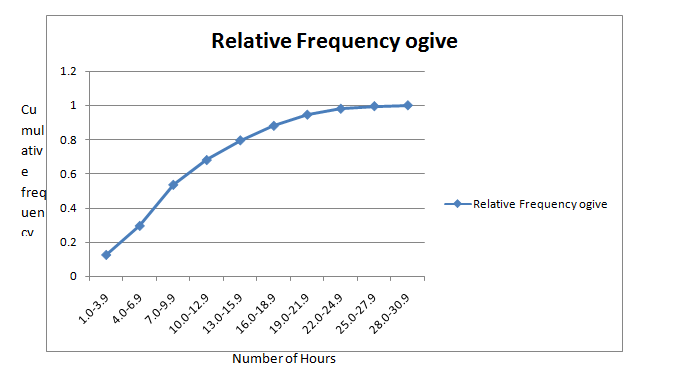
The table of cumulative relative frequency for the National league frequency distribution is given by

Batting average	Cumulative relative Frequency
0.180-0.199	0.014
0.200-0.219	0.063
0.220-0.239	0.203
0.240-0.259	0.406
0.260-0.279	0.629
0.280-0.299	0.839
0.300-0.319	0.958
0.320-0.339	0.993
0.340-0.359	1.000

The relative frequency ogivefor National League is given by