Chapter 2.2, Problem 18E

Protein Grams in Fast Food The amount of protein (in grams) for a variety of fast-food sandwiches is reported here. Construct a frequency distribution, using 6 classes. Draw a histogram, a frequency polygon, and an ogive for the data, using relative frequencies. Describe the shape of the histogram.

To determine

To Sketch: A histogram, frequency polygon and ogive using relative frequency and describe the shape of the histogram for the given data.

Answer to Problem 18E

The sketches of all three graphs are as follows:

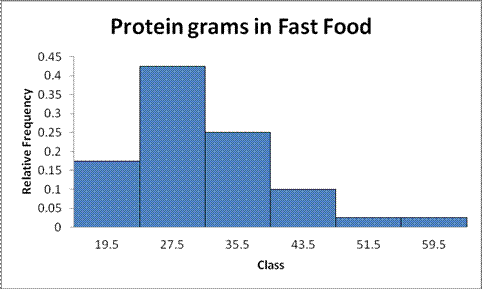
The shape of the histogram is right skewed.

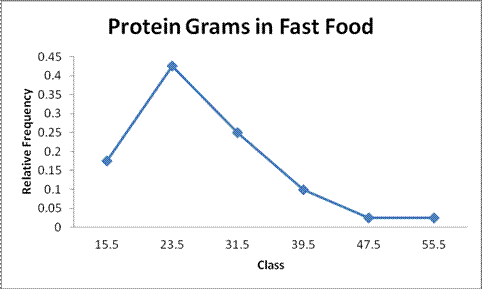
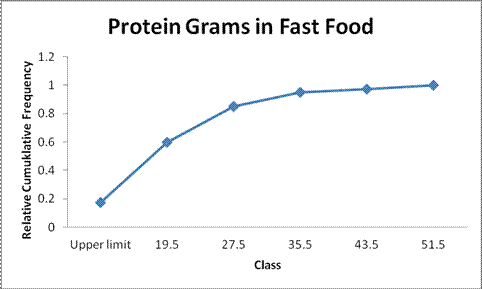
Explanation of Solution

Given Info:

The amount of protein (in grams) for a variety of fast-food sandwiches is reported here

23	30	20	27	44	26	35	20	29	29
25	15	18	27	19	22	12	26	34	15
27	35	26	43	35	14	24	12	23	31
40	35	38	57	22	42	24	21	27	33

Calculation:

The class boundaries for any class are given by:

$\begin{array}{l}\text{Upper}\text{class}\text{boundary}=\text{Upper}\text{class}\text{limit}+0.5\\ \text{Lower}\text{class}\text{boundary}=\text{Lower}\text{class}\text{limit}-0.5\end{array}$

The grouped frequency distribution is as follows:

Class limit	Class boundaries	Tally	Frequency
12-19	11.5-19.5		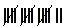7
20-27	19.5-27.5		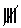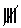17
28-35	27.5-35.5		10
36-43	35.5-43.5	$\left|\right|\left|\right|$	4
44-51	43.5-51.5	$|$	1
52-59	51.5-59.5	$|$	1

Class midpoint:

The midpoint of class boundaries is obtained by adding lower and upper limit and dividing by 2.

For the first class,

$\begin{array}{c}{X}_m=\frac{\text{Lower boundary + Upper boundary}}{2}\\ =\frac{12+19}{2}\\ =\frac{31}{2}\\ =15.5\end{array}$

Thus, the midpoint for the first class is 22.

Similarly, the midpoint for other classes was obtained.

Relative frequency distribution:

The relative frequency is the ration of a class frequency to the total frequency. Cumulative relative frequency can also defined as the sum of all previous frequencies up to the current point.

Class boundaries	Frequency	Mid point	Relative frequency	Cumulative relative frequency
11.5-19.5	7	15.5	0.175	0.175
19.5-27.5	17	23.5	0.425	0.6
27.5-35.5	10	31.5	0.25	0.85
35.5-43.5	4	39.5	0.1	0.95
43.5-51.5	1	47.5	0.025	0.975
51.5-59.5	1	55.5	0.025	1
Total	40

The histogram is a graph that displays the data by using contiguous vertical bars of various heights to represent the frequencies of the classes.

Upper limit	Relative frequency
19.5	0.175
27.5	0.425
35.5	0.25
43.5	0.1
51.5	0.025
59.5	0.025

Histogram:

Software procedure:

Step by step procedure for constructing histogram using Excel is given below:

• Press [Ctrl]-N for a new workbook.
• Enter the data in column A, one number per cell.
• Enter the upper boundaries into column B.
• From the toolbar, select the Data tab, then select Data Analysis.
• In Data Analysis, select Histogram and click [OK].
• In the Histogram dialog box, select relative column in the Input Range box and select upper limit column in the Bin Range box.
• Select New Worksheet Ply and Chart Output. Click [OK].

Output obtained from Excel is given below:

Shape of the distribution:

Symmetric:

A distribution is said to be symmetric if the left side of histogram is the mirror image of the right side of histogram.

Skewed right:

If the right side of the distribution extends far away than the left side of histogram, it is said to be skewed right.

Skewed left:

If the left side of the distribution extends far away than the right side of histogram, it is said to be skewed left.

Here, the histogram extends far away than the left side of histogram, it is said to be skewed right.

Hence, the distribution for the amount of protein (in grams) for a variety of fast-food sandwiches is skewed right.

Frequency polygons:

Step by step procedure for constructing frequency polygon using Excel is given below:

• Press [CTRL]-N for a new notebook.
• Enter the midpoints of the data into column A and the frequencies into column B including labels.
• Press and hold the left mouse button, and drag over the Frequencies (including the label) from column B.
• Select the Insert tab from the toolbar and the Line Chart option.
• Select the 2-D line chart type.

Output obtained from Excel is given below:

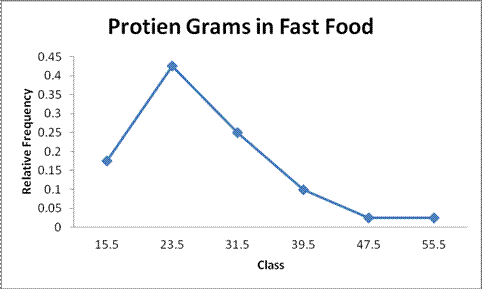
Frequency ogive:

Step by step procedure for constructing frequency ogive using Excel is given below:

• To create an ogive, use the upper class boundaries (horizontal axis) and cumulative frequencies (vertical axis) from the frequency distribution.
• Type the upper class boundaries (including a class with frequency 0 before the lowest class to anchor the graph to the horizontal axis) and
• Corresponding cumulative frequencies into adjacent columns of an Excel worksheet.
• Press and hold the left mouse button, and drag over the Cumulative Frequencies from column B.
• Select Line Chart, then the 2-D Line option.

Output obtained from Excel is given below:

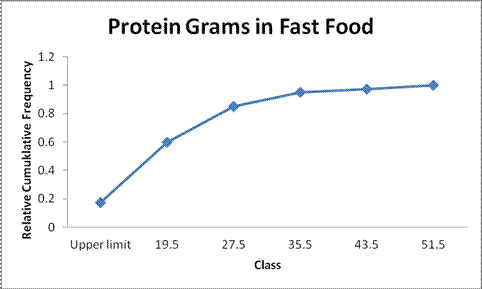
The points plotted are the upper class limit and the corresponding cumulative relative frequency.