Chapter 21, Problem 38P

(a)

To determine

The electric field at the distance of $-2.0\text{m}$ .

Explanation of Solution

Given:

The magnitude of the two point charges is $+4.0\text{μC}$ .

The position of the first point charge is at $\left(8.0\text{m},0\right)$ .

The position of the third charge is $-2.0\text{m}$ .

Formula used:

Write the expression for the superposition of the electric field.

  $\overrightarrow{E}={\overrightarrow{E}}_{Q_1}+{\overrightarrow{E}}_{Q_2}$ ..................(1)

Here, $\overrightarrow{E}$ is the resultant electric field, ${\overrightarrow{E}}_{Q_1}$ is the electric field due to first charge and ${\overrightarrow{E}}_{Q_2}$ is the electric field due to second charge.

Assume $x$ is the distance between the position of the third charge and the origin $L$ is the distance between the first and the second charge.

Write the expression for the electric field of the first charge.

  ${\overrightarrow{E}}_{Q_1}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$

Here, $k$ is the constant, $q_1$ is the first charge kept at the origin and $x$ is the distance between the positions where the third charge is kept from the origin.

Write the expression for the electric field of the second charge.

  ${\overrightarrow{E}}_{Q_2}=\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

Here, $L$ is the distance between the origin and the second charge.

Substitute $\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$ for ${\overrightarrow{E}}_{Q_1}$ and $\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$ for ${\overrightarrow{E}}_{Q_2}$ in equation (1).

  $\overrightarrow{E}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

The magnitude of $q_1$ and $q_2$ are equal.

Substitute $q$ for $q_1$ and $q_2$ in the above equation.

  $\overrightarrow{E}=kq\left[\frac{1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{1}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}\right]$ ..................(2) Calculation:

Substitute $8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}$ for $k$, $+4.0\text{μC}$ for $q$ , $8.0\text{m}$ for $L$ and $-2.0\text{m}$ for $x$ in equation (2).

  $\begin{array}{l}\overrightarrow{E}=\left(8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}\right)4.0\text{μC}\left[\frac{1}{{\left(-2.0\text{m}\right)}^2}\left(-\widehat{i}\right)+\frac{1}{{\left[8.0\text{m}-\left(-2.0\text{m}\right)\right]}^2}\left(-\widehat{i}\right)\right]\\ \overrightarrow{E}=-\left(9.4\text{kN}/\text{C}\right)\widehat{i}\end{array}$

Conclusion:

The electric field at the distance of $-2.0\text{m}$ is $-\left(9.4\text{kN}/\text{C}\right)\widehat{i}$

(b)

To determine

The electric field at the distance of $2.0\text{m}$ .

Explanation of Solution

Given:

The magnitude of the two point charges is $+4.0\text{μC}$ .

The position of the first point charge is at $\left(8.0\text{m},0\right)$ .

The position of the third charge is $2.0\text{m}$ .

Formula used:

Write the expression for the superposition of the electric field.

  $\overrightarrow{E}={\overrightarrow{E}}_{Q_1}+{\overrightarrow{E}}_{Q_2}$

Here, $\overrightarrow{E}$ is the resultant electric field, ${\overrightarrow{E}}_{Q_1}$ is the electric field due to first charge and ${\overrightarrow{E}}_{Q_2}$ is the electric field due to second charge.

Assume $x$ is the distance between the position of the third charge and the origin $L$ is the distance between the first and the second charge.

Write the expression for the electric field of the first charge.

  ${\overrightarrow{E}}_{Q_1}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$

Here, $k$ is the constant, $q_1$ is the first charge kept at the origin and $x$ is the distance between the positions where the third charge is kept from the origin.

Write the expression for the electric field of the second charge.

  ${\overrightarrow{E}}_{Q_2}=\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

Here, $L$ is the distance between the origin and the second charge.

Substitute $\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$ for ${\overrightarrow{E}}_{Q_1}$ and $\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$ for ${\overrightarrow{E}}_{Q_2}$ in equation (1).

  $\overrightarrow{E}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

The magnitude of $q_1$ and $q_2$ are equal.

Substitute $q$ for $q_1$ and $q_2$ in the above equation.

  $\overrightarrow{E}=kq\left[\frac{1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{1}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}\right]$

Calculation:

Substitute $8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}$ for $k$, $+4.0\text{μC}$ for $q$ , $8.0\text{m}$ for $L$ and $2.0\text{m}$ for $x$ in equation (2).

  $\begin{array}{l}\overrightarrow{E}=\left(8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}\right)4.0\text{μC}\left[\frac{1}{{\left(2.0\text{m}\right)}^2}\left(\widehat{i}\right)+\frac{1}{{\left[8.0\text{m}-\left(2.0\text{m}\right)\right]}^2}\left(-\widehat{i}\right)\right]\\ \overrightarrow{E}=\left(8.0\text{kN}/\text{C}\right)\widehat{i}\end{array}$

Conclusion:

The electric field at the distance of $2.0\text{m}$ is $\left(8.0\text{kN}/\text{C}\right)\widehat{i}$ .

(c)

To determine

The electric field at the distance of $6.0\text{m}$ .

Explanation of Solution

Given:

The magnitude of the two point charges is $+4.0\text{μC}$ .

The position of the first point charge is at $\left(8.0\text{m},0\right)$ .

The position of the third charge is $6.0\text{m}$ .

Formula used:

Write the expression for the superposition of the electric field.

  $\overrightarrow{E}={\overrightarrow{E}}_{Q_1}+{\overrightarrow{E}}_{Q_2}$

Here, $\overrightarrow{E}$ is the resultant electric field, ${\overrightarrow{E}}_{Q_1}$ is the electric field due to first charge and ${\overrightarrow{E}}_{Q_2}$ is the electric field due to second charge.

Assume $x$ is the distance between the position of the third charge and the origin $L$ is the distance between the first and the second charge.

Write the expression for the electric field of the first charge.

  ${\overrightarrow{E}}_{Q_1}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$

Here, $k$ is the constant, $q_1$ is the first charge kept at the origin and $x$ is the distance between the positions where the third charge is kept from the origin.

Write the expression for the electric field of the second charge.

  ${\overrightarrow{E}}_{Q_2}=\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

Here, $L$ is the distance between the origin and the second charge.

Substitute $\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$ for ${\overrightarrow{E}}_{Q_1}$ and $\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$ for ${\overrightarrow{E}}_{Q_2}$ in equation (1).

  $\overrightarrow{E}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

The magnitude of $q_1$ and $q_2$ are equal.

Substitute $q$ for $q_1$ and $q_2$ in the above equation.

  $\overrightarrow{E}=kq\left[\frac{1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{1}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}\right]$

Calculation:

Substitute $8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}$ for $k$, $+4.0\text{μC}$ for $q$ , $8.0\text{m}$ for $L$ and $6.0\text{m}$ for $x$ in equation (2).

  $\begin{array}{l}\overrightarrow{E}=\left(8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}\right)4.0\text{μC}\left[\frac{1}{{\left(6.0\text{m}\right)}^2}\left(\widehat{i}\right)+\frac{1}{{\left[8.0\text{m}-\left(6.0\text{m}\right)\right]}^2}\left(-\widehat{i}\right)\right]\\ \overrightarrow{E}=\left(8.0\text{kN}/\text{C}\right)\left(-\widehat{i}\right)\end{array}$

Conclusion:

The electric field at the distance of $6.0\text{m}$ is $\left(8.0\text{kN}/\text{C}\right)\left(-\widehat{i}\right)$ .

(d)

To determine

The electric field at the distance of $6.0\text{m}$ .

Explanation of Solution

Given:

The magnitude of the two point charges is $+4.0\text{μC}$ .

The position of the first point charge is at $\left(8.0\text{m},0\right)$ .

The position of the third charge is $10.0\text{m}$ .

Formula used:

Write the expression for the superposition of the electric field.

  $\overrightarrow{E}={\overrightarrow{E}}_{Q_1}+{\overrightarrow{E}}_{Q_2}$

Here, $\overrightarrow{E}$ is the resultant electric field, ${\overrightarrow{E}}_{Q_1}$ is the electric field due to first charge and ${\overrightarrow{E}}_{Q_2}$ is the electric field due to second charge.

Assume $x$ is the distance between the position of the third charge and the origin $L$ is the distance between the first and the second charge.

Write the expression for the electric field of the first charge.

  ${\overrightarrow{E}}_{Q_1}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$

Here, $k$ is the constant, $q_1$ is the first charge kept at the origin and $x$ is the distance between the positions where the third charge is kept from the origin.

Write the expression for the electric field of the second charge.

  ${\overrightarrow{E}}_{Q_2}=\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

Here, $L$ is the distance between the origin and the second charge.

Substitute $\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}$ for ${\overrightarrow{E}}_{Q_1}$ and $\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$ for ${\overrightarrow{E}}_{Q_2}$ in equation (1).

  $\overrightarrow{E}=\frac{k{q}_1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{k{q}_2}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}$

The magnitude of $q_1$ and $q_2$ are equal.

Substitute $q$ for $q_1$ and $q_2$ in the above equation.

  $\overrightarrow{E}=kq\left[\frac{1}{x^2}{\widehat{r}}_{q_{{}_1,p}}+\frac{1}{{\left[L-x\right]}^2}{\widehat{r}}_{q_2,p}\right]$

Calculation:

Substitute $8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}$ for $k$, $+4.0\text{μC}$ for $q$ , $8.0\text{m}$ for $L$ and $6.0\text{m}$ for $x$ in equation (2).

  $\begin{array}{l}\overrightarrow{E}=\left(8.988\times {10}^9{\text{Nm}}^{\text{2}}/{\text{C}}^{\text{2}}\right)4.0\text{μC}\left[\frac{1}{{\left(6.0\text{m}\right)}^2}\left(\widehat{i}\right)+\frac{1}{{\left[8.0\text{m}-\left(10.0\text{m}\right)\right]}^2}\left(\widehat{i}\right)\right]\\ \overrightarrow{E}=\left(9.4\text{kN}/\text{C}\right)\widehat{i}\end{array}$

Conclusion:

The electric field at the distance of $10.0\text{m}$ is $\left(9.4\text{kN}/\text{C}\right)\widehat{i}$ .

(e)

To determine

The position on the x axis where the electric field is zero.

Explanation of Solution

Given:

Electric field is zero.

Introduction:

Electric field is the region near the charge where the other object will experience a force. The direction of the electric field is in the direction of force. It is basically defined as the electric force per unit charge.

The electric field is zero at the symmetry on the x axis and that is at $4.0\text{m}$ . Electric field is positive or can be zero but is never negative.

Conclusion:

The electric field is zero at the $4.0\text{m}$ .

(f)

To determine

The sketch of electric field versus distance.

Explanation of Solution

Introduction:

Electric field is the region near the charge where the other object will experience a force. The direction of the electric field is in the direction of force. It is basically defined as the electric force per unit charge.

The sketch of the electric field lines and the distance is:

  

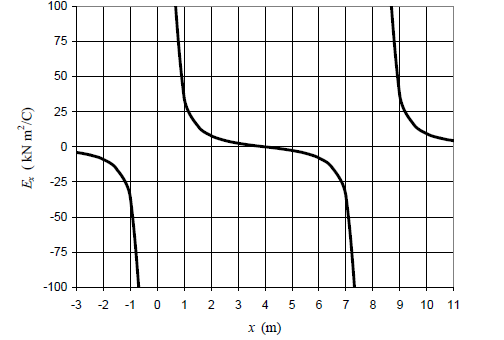
Conclusion:

Thus, the sketch ofelectric field lines and the distance is the curved lines.