Chapter 21, Problem 14P

(a)

To determine

The position $x_1$ and $x_2$ in terms of $a$ .

Explanation of Solution

Introduction:

The electric field is the region near the charge where the other object or body will experience the force. The field lines are away from the positive charge and go towards the negative charge.

Draw the representation of the position of the three charges.

  

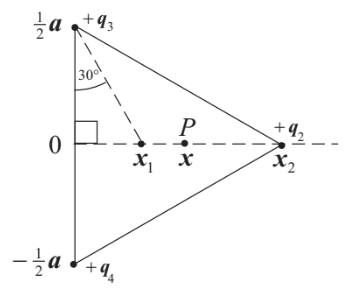
Write the expression for the Pythagoras theorem to the above triangle.

  $x_2^2+x^2=a^2$

Here, $x_2$ is the distance from the point $0$ to the charge $q_2$ and $x_1$ is the distance between the point $0$ to the third charge $q_3$ .

Substitute $\frac{1}{2}a$ for $x$ in the above equation.

  $x_2^2+{\left(\frac{1}{2}a\right)}^2=a^2$

Solve the above equation for $x_2$ .

  $x_2=\frac{\sqrt{3}}{2}a$

Write the expression for the angle.

  $\tan \theta =\frac{x_1}{x}$

Substitute $30°$ for $\theta$ and $\frac{1}{2}a$ for $x$ in the above equation.

  $\tan 30°=\frac{x_1}{\frac{1}{2}a}$

Solve the above equation for $x_1$ .

  $x_1=\frac{a}{2\sqrt{3}}$

Conclusion:

Thus, the value ofposition $x_1$ and $x_2$ in terms of $a$ are $\frac{a}{2\sqrt{3}}$ and $\frac{\sqrt{3}}{2}a$ respectively.

(b)

To determine

The electric field.

Explanation of Solution

Introduction:

The electric field is the region near the charge where the other object or body will experience the force. The field lines are away from the positive charge and go towards the negative charge.

Write the expression for the net electric field at point $P$ .

  ${\overrightarrow{E}}_P={\overrightarrow{E}}_2+{\overrightarrow{E}}_3+{\overrightarrow{E}}_4$   ........ (2)

Here, ${\overrightarrow{E}}_2$ is the electric field due to the charge $q_2$ , ${\overrightarrow{E}}_3$ is the electric field due to the charge $q_3$ and ${\overrightarrow{E}}_4$ is the electric field due to the fourth charge.

Write the expression for the electric field due to the second charge.

  ${\overrightarrow{E}}_2=\frac{k{q}_2}{r_{2,p}^3}{\widehat{r}}_{2,p}$

Here, $r_{2.p}$ is the distance between the point $p$ and the charge $q_2$ .

Substitute $x_2-x$ for $r_{2.p}$ in the above equation.

  $\begin{array}{l}{\overrightarrow{E}}_2=\frac{k{q}_2}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^3}\left(x-\frac{\sqrt{3}}{2}a\right)\widehat{i}\\ {\overrightarrow{E}}_2=\frac{-kq}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}\widehat{i}\end{array}$

Write the expression for the electric field due to the third charge.

  ${\overrightarrow{E}}_3=\frac{k{q}_3}{r_{3,p}^3}{\widehat{r}}_{3,p}$

Here, $r_{3.p}$ is the distance between the point $p$ and the charge $q_3$ .

Substitute $\sqrt{x^2+\frac{1}{4}{a}^2}$ for $r_{3,p}$ in the above equation.

  ${\overrightarrow{E}}_3=\frac{k{q}_3}{{\left(x^2+\frac{1}{4}{a}^2\right)}^{\frac{3}{2}}}\left(x\widehat{i}-\frac{1}{2}a\widehat{j}\right)$

Write the expression for the electric field due to the third charge.

  ${\overrightarrow{E}}_4=\frac{k{q}_4}{r_{4,p}^3}{\widehat{r}}_{4,p}$

Here, $r_{4.p}$ is the distance between the point $p$ and the charge $q_4$ .

Substitute $\sqrt{x^2+\frac{1}{4}{a}^2}$ for $r_{4,p}$ in the above equation.

  ${\overrightarrow{E}}_4=\frac{k{q}_4}{{\left(x^2+\frac{1}{4}{a}^2\right)}^{\frac{3}{2}}}\left(x\widehat{i}+\frac{1}{2}a\widehat{j}\right)$

Substitute $\frac{-kq}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}\widehat{i}$ for ${\overrightarrow{E}}_2$ , $\frac{k{q}_3}{{\left(x^2+\frac{1}{4}{a}^2\right)}^{\frac{3}{2}}}\left(x\widehat{i}-\frac{1}{2}a\widehat{j}\right)$ for and $\frac{k{q}_4}{{\left(x^2+\frac{1}{4}{a}^2\right)}^{\frac{3}{2}}}\left(x\widehat{i}+\frac{1}{2}a\widehat{j}\right)$ for ${\overrightarrow{E}}_4$ in equation (2).

  $\begin{array}{l}{\overrightarrow{E}}_P=\frac{-kq}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}\widehat{i}+\frac{k{q}_3}{{\left(x^2+\frac{1}{4}{a}^2\right)}^{\frac{3}{2}}}\left(x\widehat{i}-\frac{1}{2}a\widehat{j}\right)+\frac{k{q}_4}{{\left(x^2+\frac{1}{4}{a}^2\right)}^{\frac{3}{2}}}\left(x\widehat{i}+\frac{1}{2}a\widehat{j}\right)\\ {\overrightarrow{E}}_P=kq\left(\frac{-1}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}+\frac{2x}{{\left(x^2+\frac{a^2}{4}\right)}^{\frac{3}{2}}}\right)\widehat{i}\end{array}$

Conclusion:

Thus, the value of electric field is $kq\left(\frac{-1}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}+\frac{2x}{{\left(x^2+\frac{a^2}{4}\right)}^{\frac{3}{2}}}\right)\widehat{i}$ .

(c)

To determine

The electric field is same at $x=0$ and $x=x_1$ .

Explanation of Solution

Formula used:

Write the expression for the electric field at point $P$ .

  ${\overrightarrow{E}}_P=kq\left(\frac{-1}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}+\frac{2x}{{\left(x^2+\frac{a^2}{4}\right)}^{\frac{3}{2}}}\right)\widehat{i}$   ........ (4)

Calculation:

Substitute $0$ for $x$ in equation (4).

  ${\overrightarrow{E}}_P=\frac{-kq}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}\widehat{i}$

Substitute $\sqrt{\frac{3}{6}}a$ for $x_1$ in equation (4).

  $\begin{array}{l}{\overrightarrow{E}}_P=kq\left(\frac{-1}{{\left(\frac{\sqrt{3}}{2}a-x\right)}^2}+\frac{2\sqrt{\frac{3}{6}}a}{{\left(x^2+\frac{a^2}{4}\right)}^{\frac{3}{2}}}\right)\widehat{i}\\ {\overrightarrow{E}}_P=kq\left(\frac{-3}{a^2}+\frac{3}{a^2}\right)\widehat{i}\\ {\overrightarrow{E}}_P=0\end{array}$

Conclusion:

Thus, the electric field is zero.