
A sample of a monatomic ideal gas occupies 5.00 L at atmospheric pressure and 300 K (point A in Fig. P21.65). It is warmed at constant volume to 3.00 atm (point B). Then it is allowed to expand isothermally to 1.00 atm (point C) and at last compressed isobarically to its original state, (a) Find the number of moles in the sample.
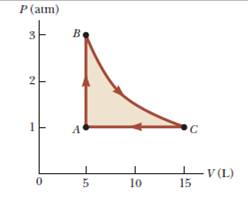
Find (b) the temperature at point B, (c) the temperature at point C, and (d) the volume at point C. (e) Now consider the processes A → B, B→ C, and C → A. Describe how to carry out each process experimentally, (f) Find Q, W, and ΔEint for each of the processes, (g) For the whole cycle A→ B→ C→ A, find Q, W, and ΔEint.
(a)
The number of moles in the sample.
Answer to Problem 21.65AP
The number of moles in the sample is
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
The number of moles in the ideal gas equation is,
Here,
The value of the ideal gas constant is
Substitute
Conclusion:
Therefore, the number of moles in the sample is
(b)
The temperature at point
Answer to Problem 21.65AP
The temperature at point
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
In the process from point
The expression for the process from point
Here,
Substitute
Conclusion:
Therefore, the temperature at point
(c)
The temperature at point
Answer to Problem 21.65AP
The temperature at point
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
In the process from point
So, the temperature at point
Conclusion:
Therefore, the temperature at point
(d)
The volume at point
Answer to Problem 21.65AP
The volume at point
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
In the process from point
The expression for the process from point
Here,
Substitute
Conclusion:
Therefore, the volume at point
(e)
The experimental methods to carry out the process
Answer to Problem 21.65AP
The experimental method to carry out the process
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
In the process from point
The volume does not change. The temperature varies from
In the process from point
The temperature does not change. The pressure varies from
In the process from point
The pressure does not change. The temperature varies from
Conclusion:
Therefore, the experimental method to carry out the process
(f)
The heat
Answer to Problem 21.65AP
The heat
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
For the process from point
The volume of gas does not change.
The work done is,
The change in internal energy is equal to the heat.
The expression for the change in internal energy is,
Here,
Substitute
Substitute
Thus, change in internal energy in process from point
For the process from point
The temperature does not change.
The change in internal energy is,
The expression of the work done is,
Substitute
Thus the change in internal energy in process from point
For the process from point
The formula of work done is,
Substitute
Thus, the work done for the point
The formula for the change in kinetic energy is,
Substitute
The heat obtain in this process is,
Conclusion:
Therefore, the heat
(g)
The heat
Answer to Problem 21.65AP
For the whole cycle
Explanation of Solution
Given info: The volume of the monatomic ideal gas is
The expression for the heat in complete cycle is,
Substitute
Thus, the heat in cycle is
The expression for the work done in complete cycle is,
Substitute
Thus, the total work done is
As the process is cyclic, the change in internal energy will be zero.
Conclusion:
Therefore, For the whole cycle
Want to see more full solutions like this?
Chapter 21 Solutions
PHYSICS 1250 PACKAGE >CI<
- How can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forward
- look at answer show all work step by steparrow_forwardLook at the answer and please show all work step by steparrow_forward3. As a woman, who's eyes are h = 1.5 m above the ground, looks down the road sees a tree with height H = 9.0 m. Below the tree is what appears to be a reflection of the tree. The observation of this apparent reflection gives the illusion of water on the roadway. This effect is commonly called a mirage. Use the results of questions 1 and 2 and the principle of ray reversibility to analyze the diagram below. Assume that light leaving the top of the tree bends toward the horizontal until it just grazes ground level. After that, the ray bends upward eventually reaching the woman's eyes. The woman interprets this incoming light as if it came from an image of the tree. Determine the size, H', of the image. (Answer 8.8 m) please show all work step by steparrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning



