University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
14th Edition
ISBN: 9780321982582
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 20, Problem 20.41P
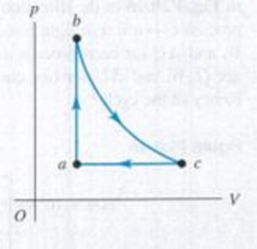
CALC A heal engine Operates using the cycle shown in Fig. P20.41. The working substance is 2 00 mol of helium gas, which reaches a maximum temperature of 327°C. Assume the helium can be treated as an ideal gas. Process bc is isothermal. The pressure in states a and c is 100 × 105 Pa. and the pressure in state b is 3.00 × 105 Pa. (a) How much heat enters the gas and how much leaves the gas each cycle? (b) How much work does the engine do each cycle, and what is its efficiency? (c) Compare this engine’s efficiency with the maximum possible efficiency attainable with the hot and cold reservoirs used by this cycle.
Figure P20.41
Expert Solution & Answer
Trending nowThis is a popular solution!
Learn your wayIncludes step-by-step video
schedule09:14
Chapter 20 Solutions
University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
Ch. 20.1 - Your left and right hands are normally at the same...Ch. 20.2 - Rank the following heat engines in order from...Ch. 20.3 - For an Otto-cycle engine with cylinders of a fixed...Ch. 20.4 - Can you cool your house by leaving the...Ch. 20.5 - Would a 100%-efficient engine (Fig. 20.11a)...Ch. 20.6 - An inventor looking for financial support comes to...Ch. 20.7 - Suppose 2.00 kg of water at 50C spontaneously...Ch. 20.8 - A quantity of N molecules of an ideal gas...Ch. 20 - A pot is half-filled with water, and a lid is...Ch. 20 - Prob. 20.2DQ
Ch. 20 - Prob. 20.3DQCh. 20 - Prob. 20.4DQCh. 20 - Why must a room air conditioner be placed in a...Ch. 20 - Prob. 20.6DQCh. 20 - Prob. 20.7DQCh. 20 - An electric motor has its shaft coupled to that of...Ch. 20 - When a wet cloth is hung up in a hot wind in the...Ch. 20 - Compare the pV-diagram for the Otto cycle in Fig....Ch. 20 - The efficiency of heat engines is high when the...Ch. 20 - What would be the efficiency of a Carnot engine...Ch. 20 - Real heat engines, like the gasoline engine in a...Ch. 20 - Does a refrigerator full of food consume more...Ch. 20 - In Example 20.4, a Carnot refrigerator requires a...Ch. 20 - How can the thermal conduction of heat from a hot...Ch. 20 - Explain why each of the following processes is an...Ch. 20 - The free expansion of an ideal gas is an adiabatic...Ch. 20 - Are the earth and sun in thermal equilibrium? Are...Ch. 20 - Prob. 20.20DQCh. 20 - Prob. 20.21DQCh. 20 - Prob. 20.22DQCh. 20 - BIO A growing plant creates a highly complex and...Ch. 20 - A diesel engine performs 2200 J of mechanical work...Ch. 20 - An aircraft engine takes in 9000 J of heat and...Ch. 20 - A Gasoline Engine. A gasoline engine takes in 1.61...Ch. 20 - A gasoline engine has a power output of 180 kW...Ch. 20 - The pV-diagram in Fig. E20.5 shows a cycle of heat...Ch. 20 - (a) Calculate the theoretical efficiency for an...Ch. 20 - The Otto-cycle engine in a Mercedes-Benz SL1 a...Ch. 20 - Section 20.4 Refrigerators 20.8The coefficient of...Ch. 20 - A refrigerator has a coefficient of performance of...Ch. 20 - A freezer has a coefficient of performance of...Ch. 20 - A refrigerator has a coefficient of performance of...Ch. 20 - A Carnot engine is operated between two heat...Ch. 20 - A Carnot engine whose high-temperature reservoir...Ch. 20 - An ice-making machine operates in a Carnot cycle....Ch. 20 - A Carnot engine has an efficiency of 66% and...Ch. 20 - A certain brand of freezer is advertised to use...Ch. 20 - A Carnot refrigerator is operated between two heat...Ch. 20 - A Carnot heat engine uses a hot reservoir...Ch. 20 - You design an engine that takes in 1.50 104 J of...Ch. 20 - A 4.50-kg block of ice at 0.00C falls into the...Ch. 20 - A sophomore with nothing better to do adds heat to...Ch. 20 - CALC You decide to take a nice hot bath but...Ch. 20 - A 15.0-kg block of ice at 0.0C melts to liquid...Ch. 20 - CALC You make tea with 0.250 kg of 85.0C water and...Ch. 20 - Three moles of an ideal gas undergo a reversible...Ch. 20 - What is the change in entropy of 0.130 kg of...Ch. 20 - (a) Calculate the change in entropy when 1.00 kg...Ch. 20 - Entropy Change Due to Driving. Premium gasoline...Ch. 20 - CALC Two moles of an ideal gas occupy a volume V....Ch. 20 - A box is separated by a partition into two parts...Ch. 20 - CALC A lonely party balloon with a volume of 2.40...Ch. 20 - You are designing a Carnot engine that has 2 mol...Ch. 20 - CP An ideal Carnot engine operates between 500C...Ch. 20 - Prob. 20.34PCh. 20 - CP A certain heat engine operating on a Carnot...Ch. 20 - A heat engine takes 0.350 mol of a diatomic ideal...Ch. 20 - Prob. 20.37PCh. 20 - What is the thermal efficiency of an engine that...Ch. 20 - CALC You build a heal engine that takes 1.00 mol...Ch. 20 - CP As a budding mechanical engineer, you are...Ch. 20 - CALC A heal engine Operates using the cycle shown...Ch. 20 - CP BIO Humun Entropy. A person who has skin of...Ch. 20 - An experimental power plant at the Natural Energy...Ch. 20 - CP BIO A Human Engine. You decide to use your body...Ch. 20 - CALC A cylinder contains oxygen at a pressure of...Ch. 20 - A monatomic ideal gas it taken around the cycle...Ch. 20 - A Carnot engine operates between two heat...Ch. 20 - A typical coal-fired power plant generates 1000 MW...Ch. 20 - Automotive Thermodynamics. A Volkswagen Passat has...Ch. 20 - An air conditioner operates on 800 W of power and...Ch. 20 - The pV-diagram in Fig. P20.51 shows the cycle for...Ch. 20 - BIO Human Entropy. A person with skin of surface...Ch. 20 - CALC An object of mass m1, specific heat c1, and...Ch. 20 - CALC To heat 1 cup of water (250 cm3) to make...Ch. 20 - DATA In your summer job with a venture capital...Ch. 20 - DATA For a refrigerator or air conditioner, the...Ch. 20 - DATA You are conducting experiments to study...Ch. 20 - Consider a Diesel cycle that starts (at point a in...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...
Additional Science Textbook Solutions
Find more solutions based on key concepts
37.30 An electron is acted upon by a force of 5.00 × 10?15 N due to an electric field. Find the acceleration th...
University Physics (14th Edition)
Write each number in scientific notation.
12. 0.00224
Applied Physics (11th Edition)
Show that and dm/dt have the same units.
University Physics Volume 2
B. Together with your classmates, take your ticker tape segments and arrange yourselves in a line, ranked accor...
Tutorials in Introductory Physics
The setup depicted in Figure 4.6 is used in a diffraction experiment using X-rays of 0.26 nm wavelength. Constr...
Modern Physics
27. A pendulum has a period of 1.85 s on Earth. Whatis its period on Mars, where the acceleration of gravity is...
Physics: Principles with Applications
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Figure P21.45 shows a cyclic process ABCDA for 1.00 mol of an ideal gas. The gas is initially at Pi = 1.50 105 Pa, Vi = 1.00 103 m3 (point A in Fig. P21.45). a. What is the net work done on the gas during the cycle? b. What is the net amount of energy added by heat to this gas during the cycle? FIGURE P21.45arrow_forwardA thermodynamic cycle is shown in Figure P21.34 for a gas in a piston. The system changes states along the path ABCA. a. What is the total work done by the gas during this cycle? b. How much heat is transferred? Does heat flow into or out of the system? Figure P21.34arrow_forwardAn ideal gas with specific heat ratio confined to a cylinder is put through a closed cycle. Initially, the gas is at Pi, Vi, and Ti. First, its pressure is tripled under constant volume. It then expands adiabatically to its original pressure and finally is compressed isobarically to its original volume. (a) Draw a PV diagram of this cycle. (b) Determine the volume at the end of the adiabatic expansion. Find (c) the temperature of the gas at the start of the adiabatic expansion and (d) the temperature at the end of the cycle. (e) What was the net work done on the gas for this cycle?arrow_forward
- Figure P22.73 illustrates the cycle ABCA for a 2.00-mol sample of an ideal diatomic gas, where the process CA is a reversible isothermal expansion. What is a. the net work done by the gas during one cycle? b. How much energy is added to the gas by heat during one cycle? c. How much energy is exhausted from the gas by heat during one cycle? d. What is the efficiency of the cycle? e. What would be the efficiency of a Carnot engine operated between the temperatures at points A and B during each cycle?arrow_forwardOf the following, which is not a statement of the second law of thermodynamics? (a) No heat engine operating in a cycle can absorb energy from a reservoir and use it entirely to do work, (b) No real engine operating between two energy reservoirs can be more efficient than a Carnot engine operating between the same two reservoirs, (c) When a system undergoes a change in state, the change in the internal energy of the system is the sum of the energy transferred to the system by heat and the work done on the system, (d) The entropy of the Universe increases in all natural processes, (e) Energy will not spontaneously transfer by heat from a cold object to a hot object.arrow_forwardAt point A in a Carnot cycle, 2.34 mol of a monatomic ideal gas has a pressure of 1 4000 kPa, a volume of 10.0 L, and a temperature of 720 K. The gas expands isothermally to point B and then expands adiabatically to point C, where its volume is 24.0 L. An isothermal compression brings it to point D, where its volume is 15.0 L. An adiabatic process returns the gas to point A. (a) Determine all the unknown pressures, volumes, and temperatures as you f ill in the following table: (b) Find the energy added by heat, the work done by the engine, and the change in internal energy for each of the steps A B, B C, C D, and D A (c) Calculate the efficiency Wnet/|Qk|. (d) Show that the efficiency is equal to 1 - TC/TA, the Carnot efficiency.arrow_forward
- A Carnot engine employs 1.5 mol of nitrogen gas as a working substance, which is considered as an ideal diatomic gas with =7.5 at the working temperatures of the engine. The Carnot cycle goes in the cycle ABCDA with AB being an isothermal expansion. The volume at points A and C of the cycle are 5.0103 m3 and 0.15 L, respectively. The engine operates between two thermal baths of temperature 500 K 300 K. (a) Find the values of volume at B and D. (b) How much heat is absorbed by the gas in the AB isothermal expansion? (c) How much work is done by the gas in the AB isothermal expansion? (d) How much heat is given up by the gas in the CD isothermal expansion? (e) How much work is done by the gas in the CD isothermal compression? (f) How much work is done by the gas in the BC adiabatic expansion? (g) How much work is done by the gas in the DA adiabatic compression? (h) Find the value of efficiency of the engine based on the net and heat input. Compare this value to the efficiency of a Carnot engine based on the temperatures of the baths.arrow_forward(a) Determine the work done on a gas that expands from i to f as indicated in Figure P19.16. (b) What If? How much work is done on the gas if it is compressed from f to i along the same path? Figure P19.16arrow_forwardA car salesperson claims that a 300-hp engine is a necessary option in a compact car, in place of the conventional 130-hp engine. Suppose you intend to drive the car within speed limits ( 65 mi/h) on flat terrain. How would you counter this sales pitch?arrow_forward
- As shown below, calculate the work done by the gas in the quasi-static processes represented by the paths (a) AB; (b) ADB; (c) ACB; and (d) ADCB. `arrow_forwardThe compression ratio of an Otto cycle as shown in Figure 21.12 is VA/VB = 8.00. At the beginning A of the compression process, 500 cm3 of gas is at 100 kPa and 20.0C. At the beginning of the adiabatic expansion, the temperature is TC = 750C. Model the working fluid as an ideal gas with = 1.40. (a) Fill in this table to follow the states of the gas: (b) Fill in this table to follow the processes: (c) Identify the energy input |Qh|, (d) the energy exhaust |Qc|, and (e) the net output work Weng. (f) Calculate the efficiency. (g) Find the number of crankshaft revolutions per minute required for a one-cylinder engine to have an output power of 1.00 kW = 1.34 hp. Note: The thermodynamic cycle involves four piston strokes.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Thermodynamics: Crash Course Physics #23; Author: Crash Course;https://www.youtube.com/watch?v=4i1MUWJoI0U;License: Standard YouTube License, CC-BY