Chapter 2, Problem 90P

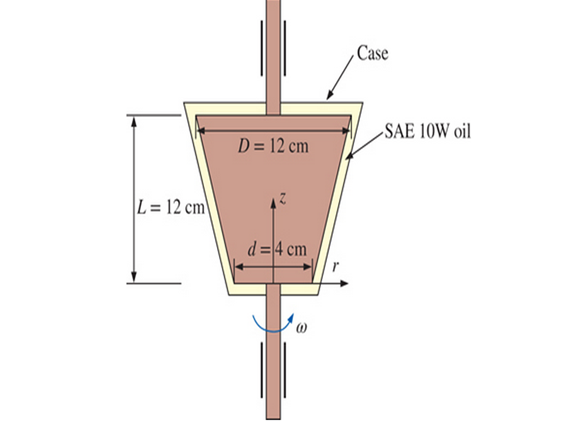
A frustum-shaped body is rotating at a constant angular speed of 200 rad/s in a container filled with SAE 10W oil at 20°C ( $\mu =0.100\text{Pa}\cdot \text{s}$ ), as shown in Fig. P2-85. If the thickness of the oil film on all sides is 1.2 mm, determine the power required to maintain this motion. Also determine the reduction in the required power input when the oil temperature rises to 80°C ( $\mu =0.0078\text{Pa}\cdot \text{s}$ ).

To determine

The torque required to rotate the inner cylinder at constant speed.

And the torque required for motion at $80°\text{C}$ viscosity.

Answer to Problem 90P

The torque required to rotate the inner cylinder at constant speed is $270.21\text{W}$.

And the torque required for motion at $80°\text{C}$ viscosity is $\text{249}\text{.14}\text{W}$.

Explanation of Solution

Given information:

The dynamic viscosity of oil at $20°\text{C}$ is $\left(0.1\text{Pa}\cdot \text{s}\right)$ $\left(0.1\text{N}\frac{\text{s}}{{\text{m}}^{\text{2}}}\right)$, dynamic viscosity of oil at $80°\text{C}$ is $\left(0.0078\text{Pa}\cdot \text{s}\right)$ $\left(0.0078\text{N}\frac{\text{s}}{{\text{m}}^{\text{2}}}\right)$, angular speed is $200\text{rad}/\text{s}$ length of the container is $12\text{cm}$ $\left(12\times {10}^{-2}\text{m}\right)$ diameter at the top of container is $12\text{cm}$ $\left(12\times {10}^{-2}\text{m}\right)$ at the bottom of container is $4\text{cm}$ $\left(4\times {10}^{-2}\text{m}\right)$, thickness of the oil film is $1.2mm$ $\left(1.2\times {10}^{-3}\text{m}\right)$.

Write the expression for shear stress on the surface of frustum.

  ${\tau }_w=\mu \frac{V}{h}$   ...... (I)

The wall shear is ${\tau }_w$, dynamic viscosity is $\mu$, tangential velocity is $V$, thickness of the oil film is $h$

Substitute $r\omega$ for $V$ in the Equation (I).

  ${\tau }_w=\mu \frac{r\omega }{h}$

Here, angular velocity of the container is $\omega$ and radius of frustum at the bottom is $r$.

Write the expression for shear force.

  $dF={\tau }_{w}dA$   ...... (II)

Here, area of the frustum is $dA$ and shear force is $dF$.

Substitute $\mu \frac{r\omega }{h}$ for ${\tau }_w$ in the Equation (II).

  $dF=\left(\frac{\mu r\omega }{h}\right)dA$   ...... (III)

Write the expression for torque developed.

  $dT=rdF$   ...... (IV)

Here, torque developed is $dT$.

Substitute $\left(\frac{\mu r\omega }{h}\right)dA$ for $dF$ in the Equation (IV).

  $\begin{array}{l}dT=r\left(\frac{\mu r\omega }{h}\right)dA\\ =\left(\frac{\mu \omega }{h}\right)r^{2}dA\end{array}$   ...... (V)

Write the expression for torque by integrating Equation (V).

  $\begin{array}{l}{\displaystyle \int dT}={\displaystyle \int \left(\frac{\mu \omega }{h}\right)r^{2}dA}\\ T=\frac{\mu w}{h}{\displaystyle {\int }_A{r}^{2}dA}\end{array}$   ...... (VI)

Write the expression for shaft power developed.

  ${\dot{W}}_{sh}=\omega T$   ...... (VII)

Here, developed shaft power is ${\dot{W}}_{sh}$.

Substitute $\frac{\mu w}{h}{\displaystyle {\int }_A{r}^{2}dA}$ in Equation (VII).

  ${\dot{W}}_{sh}=\left(\frac{\mu {\omega }^2}{h}\right){\displaystyle {\int }_A{r}^{2}dA}$   ...... (VIII)

Write the expression for shaft power for the top surface.

Substitute $2\pi rdr$ for $dA$ with limits extending from $r$ to $D/2$ in Equation (VIII).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{top}=\left(\frac{\mu {\omega }^2}{h}\right){\displaystyle {\int }_r^{D/2}{r}^2\left(2\pi rdr\right)}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right){\displaystyle {\int }_r^{D/2}{r}^{3}dr}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right){\left[\frac{r^4}{4}\right]}_r^{D/2}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{{\left(D/2\right)}^4}{4}-\frac{r^4}{4}\right]\end{array}$

  ${\left({\dot{W}}_{sh}\right)}_{top}=\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{\left(D^4\right)}{64}-\frac{r^4}{4}\right]$   ...... (IX)

Substitute $0$ for $r$ in Equation (IX).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{top}=\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{\left(D^4\right)}{64}-\frac{0^4}{4}\right]\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{\left(D^4\right)}{64}\right]\\ {\left({\dot{W}}_{sh}\right)}_{top}=\frac{\pi \mu {\omega }^2{D}^4}{32h}\end{array}$   ...... (X)

Here, diameter of frustum at the top is $D$ and shaft power for the top surface is ${\left({\dot{W}}_{sh}\right)}_{top}$.

Substitute $2\pi rdr$ for $dA$ with limits extending from $r$ to $d/2$ in Equation (VIII).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{bottom}=\left(\frac{\mu {\omega }^2}{h}\right){\displaystyle {\int }_r^{d/2}{r}^2\left(2\pi rdr\right)}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right){\displaystyle {\int }_r^{d/2}{r}^{3}dr}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right){\left[\frac{r^4}{4}\right]}_r^{d/2}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{{\left(d/2\right)}^4}{4}-\frac{r^4}{4}\right]\end{array}$

  ${\left({\dot{W}}_{sh}\right)}_{bottom}=\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{\left(d^4\right)}{64}-\frac{r^4}{4}\right]$   ...... (XI)

Here, diameter of frustum at the bottom is $d$ and shaft power for the bottom surface is ${\left({\dot{W}}_{sh}\right)}_{bottom}$.

Substitute $0$ for $r$ in Equation (XI).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{bottom}=\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{\left(d^4\right)}{64}-\frac{0^4}{4}\right]\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left[\frac{\left(d^4\right)}{64}\right]\\ {\left({\dot{W}}_{sh}\right)}_{bottom}=\frac{\pi \mu {\omega }^2{d}^4}{32h}\end{array}$   ...... (XII)

Substitute $2\pi rdz$ for $dA$ with limits extending from $d/2$ to $D/2$ in Equation (VIII).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{shide}=\left(\frac{\mu {\omega }^2}{h}\right){\displaystyle {\int }_{d/2}^{D/2}{r}^2\left(2\pi rdz\right)}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right){\displaystyle {\int }_{d/2}^{D/2}{r}^{3}dz}\end{array}$   ...... (XIII)

Here, shaft power for the side surface is ${\left({\dot{W}}_{sh}\right)}_{shide}$.

Write the expression to obtain value of $r$ in term of $z$.

  $r=\frac{d}{2}+\frac{D-d}{2L}z$

Differentiate $r$ with respect to $z$.

  $\begin{array}{c}\frac{dr}{dz}=\frac{d}{dz}\left(\frac{d}{2}+\frac{D-d}{2L}z\right)\\ \frac{dr}{dz}=0+\frac{D-d}{2L}\times 1\\ dr=\left(\frac{D-d}{2L}\right)dz\\ dz=\left(\frac{2L}{D-d}\right)dr\end{array}$   ...... (XIV)

Substitute $\left(\frac{2L}{D-d}\right)dr$ for $dz$ in Equation (XIII).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{shide}=\left(\frac{2\pi \mu {\omega }^2}{h}\right){\displaystyle {\int }_{d/2}^{D/2}{r}^3\left(\frac{2L}{D-d}\right)dr}\\ =\left(\frac{2\pi \mu {\omega }^2}{h}\right)\left(\frac{2L}{D-d}\right){\displaystyle {\int }_{d/2}^{D/2}{r}^{3}dr}\\ =\left(\frac{4L\pi \mu {\omega }^2}{h\left(D-d\right)}\right){\left[\frac{r^4}{4}\right]}_{d/2}^{D/2}\\ =\left(\frac{4L\pi \mu {\omega }^2}{h\left(D-d\right)}\right)\left[\frac{{\left(D/2\right)}^2}{4}-\frac{{\left(d/2\right)}^2}{4}\right]\end{array}$

  $\begin{array}{c}=\left(\frac{4L\pi \mu {\omega }^2}{h\left(D-d\right)}\right)\left[\frac{{\left(D/2\right)}^2}{4}-\frac{{\left(d/2\right)}^2}{4}\right]\\ {\left({\dot{W}}_{sh}\right)}_{shide}=\left(\frac{4L\pi \mu {\omega }^2}{h\left(D-d\right)}\right)\left(\frac{D^4-d^4}{16}\right)\end{array}$   ...... (XV)

Write the expression for total shaft power.

  ${\left({\dot{W}}_{sh}\right)}_{total}={\left({\dot{W}}_{sh}\right)}_{top}+{\left({\dot{W}}_{sh}\right)}_{bottom}+{\left({\dot{W}}_{sh}\right)}_{shide}$   ...... (XVI)

Substitute $\left(\frac{\pi \mu {\omega }^2{D}^4}{32h}\right)$ for ${\left({\dot{W}}_{sh}\right)}_{top}$, $\left(\frac{\pi \mu {\omega }^2{d}^4}{32h}\right)$ for ${\left({\dot{W}}_{sh}\right)}_{bottom}$, and ${\left({\dot{W}}_{sh}\right)}_{shide}$ for $\left(\frac{4L\pi \mu {\omega }^2}{h\left(D-d\right)}\right)\left(\frac{D^4-d^4}{16}\right)$ in Equation (XVI).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{total}=\left(\frac{\pi \mu {\omega }^2{D}^4}{32h}\right)+\left(\frac{\pi \mu {\omega }^2{d}^4}{32h}\right)+\left(\frac{4L\pi \mu {\omega }^2}{h\left(D-d\right)}\right)\left(\frac{D^4-d^4}{16}\right)\\ =\left(\frac{\pi \mu {\omega }^2{D}^4}{32h}\right)\left[1+{\left(\frac{d}{D}\right)}^4+\frac{2L\left(1-{\left(\frac{d}{D}\right)}^4\right)}{\left(D-d\right)}\right]\end{array}$   ...... (XVII)

Write the expression for power required to maintain the motion at $80°\text{C}$.

  ${\left({\dot{W}}_{sh}\right)}_{totalat80°\text{C}}=\frac{{\mu }_{at80°\text{C}}}{{\mu }_{at20°\text{C}}}{\left({\dot{W}}_{sh}\right)}_{total}$   ...... (XVIII)

Here, viscosity at $80°\text{C}$ is ${\mu }_{at80°\text{C}}$ and viscosity at $20°\text{C}$ is ${\mu }_{at20°\text{C}}$, and total shaft power at $80°\text{C}$ is ${\left({\dot{W}}_{sh}\right)}_{totalat80°\text{C}}$.

Write the expression for reduction in power input required when the oil pressure rise at $80°\text{C}$.

  $\text{Power}={\left({\dot{W}}_{sh}\right)}_{totalat20°\text{C}}-{\left({\dot{W}}_{sh}\right)}_{totalat20°\text{C}}$   ...... (XIX)

Here, total shaft power at $20°\text{C}$ is ${\left({\dot{W}}_{sh}\right)}_{totalat20°\text{C}}$.

Calculation:

Substitute $\left(0.1\text{N}\frac{\text{s}}{{\text{m}}^{\text{2}}}\right)$ for $\mu$, $\left(200\text{rad}/\text{s}\right)$ for $\omega$, $12\times {10}^{-2}\text{m}$ for $D^4$, $\left(1.2\times {10}^{-3}\text{m}\right)$ for $h$, $\left(3\times {10}^{-2}\text{m}\right)$ for $d^4$, $\left(12\times {10}^{-2}\text{m}\right)$ for $L$ in Equation (XVII).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{total}=\left(\frac{\pi \left(0.1\text{N}\frac{\text{s}}{{\text{m}}^{\text{2}}}\right){\left(200\text{rad}/\text{s}\right)}^2{\left(12\times {10}^{-2}\text{m}\right)}^4}{32\left(1.2\times {10}^{-3}\text{m}\right)}\right)\\ \times \left[\begin{array}{l}1+{\left(\frac{\left(3\times {10}^{-2}\text{m}\right)}{\left(12\times {10}^{-2}\text{m}\right)}\right)}^4\\ +\frac{2\left(12\times {10}^{-2}\text{m}\right)\left(1-{\left(\frac{\left(3\times {10}^{-2}\text{m}\right)}{\left(12\times {10}^{-2}\text{m}\right)}\right)}^4\right)}{\left(\left(12\times {10}^{-2}\text{m}\right)-\left(3\times {10}^{-2}\text{m}\right)\right)}\end{array}\right]\\ =67.858\left[1+0.012+2.970\right]\left(\text{N}\cdot \frac{\text{m}}{\text{s}}\right)\\ =270.21\text{W}\end{array}$

Substitute $0.0078\left(Pa\cdot s\right)$ for ${\mu }_{at80°\text{C}}$, $0.1\left(Pa\cdot s\right)$ for ${\mu }_{at20°\text{C}}$, and $270.21\text{W}$ for ${\left({\dot{W}}_{sh}\right)}_{total}$ in Equation (XVIII).

  $\begin{array}{c}{\left({\dot{W}}_{sh}\right)}_{totalat80°\text{C}}=\frac{0.0078\left(Pa\cdot s\right)}{0.1\left(Pa\cdot s\right)}\left(270.21\text{W}\right)\\ =0.078\times 270.21\text{W}\\ \text{=21}\text{.075}\text{W}\end{array}$

Substitute $270.21\text{W}$ for ${\left({\dot{W}}_{sh}\right)}_{totalat20°\text{C}}$ and $21.075\text{W}$ for ${\left({\dot{W}}_{sh}\right)}_{totalat20°\text{C}}$ in Equation (XIX).

  $\begin{array}{l}\text{Power}=270.21\text{W}-21.075\text{W}\\ \text{=249}\text{.14}\text{W}\end{array}$

Conclusion:

The torque required to rotate the inner cylinder at constant speed is $270.21\text{W}$.

And the torque required for motion at $80°\text{C}$ viscosity is $\text{249}\text{.14}\text{W}$.