Chapter 2, Problem 31P

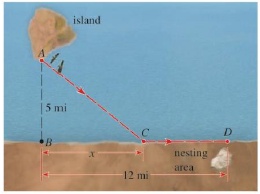
Bird Flight A bird is released from point A on an island, 5 mi from the nearest point B on a straight shoreline. The bird flies to a point C on the shoreline and then flies along the shoreline to its nesting area D (see the figure). Suppose the bird requires 10 kcal/mi of energy to fly over land and 14 kcal/mi to fly over water.

1. (a) Use the fact that

$\text{energy}\text{used}\text{=}\text{energy}\text{per}\text{mile}\text{×}\text{miles}\text{flown}$

to show that the total energy used by the bird is modeled by the function

$E(x)=14\sqrt{x^2+25}+10(12-x)$

1. (b) If the bird instinctively chooses a path that minimizes its energy expenditure, to what point does it fly?

To determine

To show: The total energy used by the bird is $E\left(x\right)=14\sqrt{x^2+25}+10\left(12-x\right)$.

Explanation of Solution

Formula used:

$\text{energy}\text{}\text{used}\text{}=\text{energy}\text{per mile }\times \text{miles}\text{}\text{flown}$ (1)

Calculation:

The energy of the bird requires $10\text{kcal/mi}$ to fly over the land and $14\text{kcal/mi}$ to fly over the water.

All the distances related to the bird are given in the figure below,

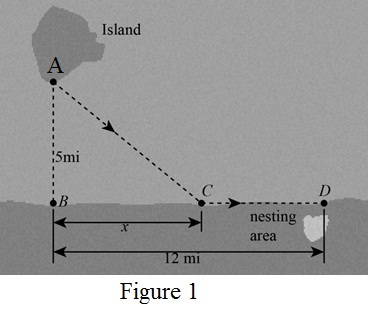
Let x be distance between point B and C.

In $\Delta \text{ABC}$,

Use the Pythagoras theorem to find the length AC.

$\begin{array}{c}A{C}^2=A{B}^2+B{C}^2[\because {\text{Hypothesis}}^2={\text{base}}^2+{\text{perpendicular}}^2]\\ ={\left(5\right)}^2+x^2\\ AC=\sqrt{25+x^2}\end{array}$

The length of the side BD is 12mi and the length of the side BC is x mi.

Then, the length of the side CD is,

$\begin{array}{c}CD=BD-BC\\ =12-x\end{array}$

The bird flies from the point C to the point D on the land with the energy $10\text{kcal/mi}$.

$\text{Energy}\text{for}\text{one}\text{mile}=10\text{kcal}$ (2)

To find the energy for $\left(12-x\right)\text{mile}$, multiply by $12-x$ both side of the equation (2),

$\text{Energy}\text{for}\left(12-x\right)\text{mile}=10\left(12-x\right)\text{kcal}$

The bird flies from the point A to the point C on the water with the energy $14\text{kcal/mi}$.

$\text{Energy}\text{for}\text{one}\text{mile}=14\text{kcal}$ (3)

To find the energy for $\sqrt{25+x^2}\text{mile}$, multiply $\sqrt{25+x^2}$ on both sides of the equation (3),

$\text{Energy}\text{for}\sqrt{25+x^2}\text{mile}=14\sqrt{25+x^2}\text{kcal}$

Then the total energy is,

$\text{Total}\text{Energy}=\text{Energy}\text{for}\left(12-x\right)\text{mile}+\text{Energy}\text{for}\sqrt{25+x^2}\text{mile}$ (4)

Substitute $10\left(12-x\right)\text{kcal}$ for $\text{Energy}\text{for}12-x\text{mile}$ and $14\sqrt{25+x^2}\text{kcal}$ for $\text{Energy}\text{for}\sqrt{25+x^2}\text{mile}$ in the equation (4),

$\begin{array}{c}\text{Total}\text{Energy}=\text{Energy}\text{for}\left(12-x\right)\text{mile}+\text{Energy}\text{for}\sqrt{25+x^2}\text{mile}\\ E\left(x\right)\text{=}10\left(12-x\right)\text{kcal}+14\sqrt{25+x^2}\text{kcal}\\ \text{=}\left(10\left(12-x\right)+14\sqrt{25+x^2}\right)\text{kcal}\end{array}$

Thus, the total energy is $E\left(x\right)=14\sqrt{x^2+25}+10\left(12-x\right)$.

To determine

To find: The path that minimizes the energy expenditure.

Answer to Problem 31P

The bird flies till the point C on shoreline which is 5.013 miles from point B and then flies along the shoreline.

Explanation of Solution

From the part (a), the total energy is $E\left(x\right)=14\sqrt{x^2+25}+10\left(12-x\right)$.

To find the minimum energy sketch the graph of $E\left(x\right)=14\sqrt{x^2+25}+10\left(12-x\right)$.

The function contains the variable x is the length of the side BC.

The local minimum value of the function is the least finite value where the value of the function at the any number is less than to the original function.

The condition for local minimum is,

$f\left(a\right)\le f\left(x\right)$

Using online graphing calculator, sketch the graph of the function $E\left(x\right)=14\sqrt{x^2+25}+10\left(12-x\right)$ as shown in the figure below.

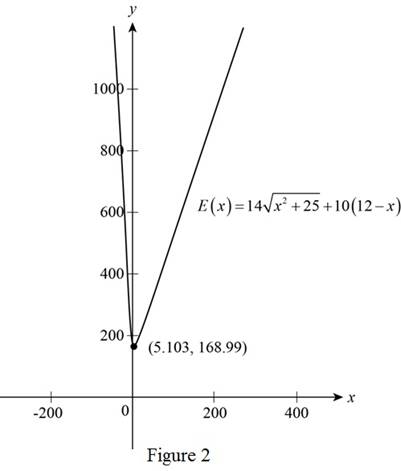
From the above figure, it can be observed that the least peak occurs at the point $\left(5.103,168.99\right)$.

Then, the minimum energy expenditure is 168.99 at $x=5.103$.

Thus, the point C is 5.103 mi away from point B.

Therefore, the bird flies till the point C on shoreline which is 5.013 miles from point B and then flies along the shoreline.