Given Data:
Refer to Figure 19.132 in the textbook for the transistor network circuit.
hie=2 kΩhre=2.5×10−4hfe=150hoe=10 μS
From the given transistor network circuit, the internal resistance (Rs) is 1 kΩ, emitter resistance (Re) is 0.2 kΩ, which is 200 Ω, and the load resistance (RL) is 3.8 kΩ.
Formula used:
Refer to Equation 19.73 in the textbook and write the expression for voltage gain of a transistor network in terms of hybrid parameters as follows:
Av=VcVb (1)
Here,
Vc is the collector voltage, which is the output voltage and
Vb is the base voltage.
Write the expression for current gain of the transistor network as follows:
Ai=IcIb (2)
Here,
Ib is the base current and
Ic is the collector current.
Write the expression for input impedance of the transistor network as follows:
Zin=VbIb (3)
Calculation:
Redraw the given circuit as shown in Figure 1.
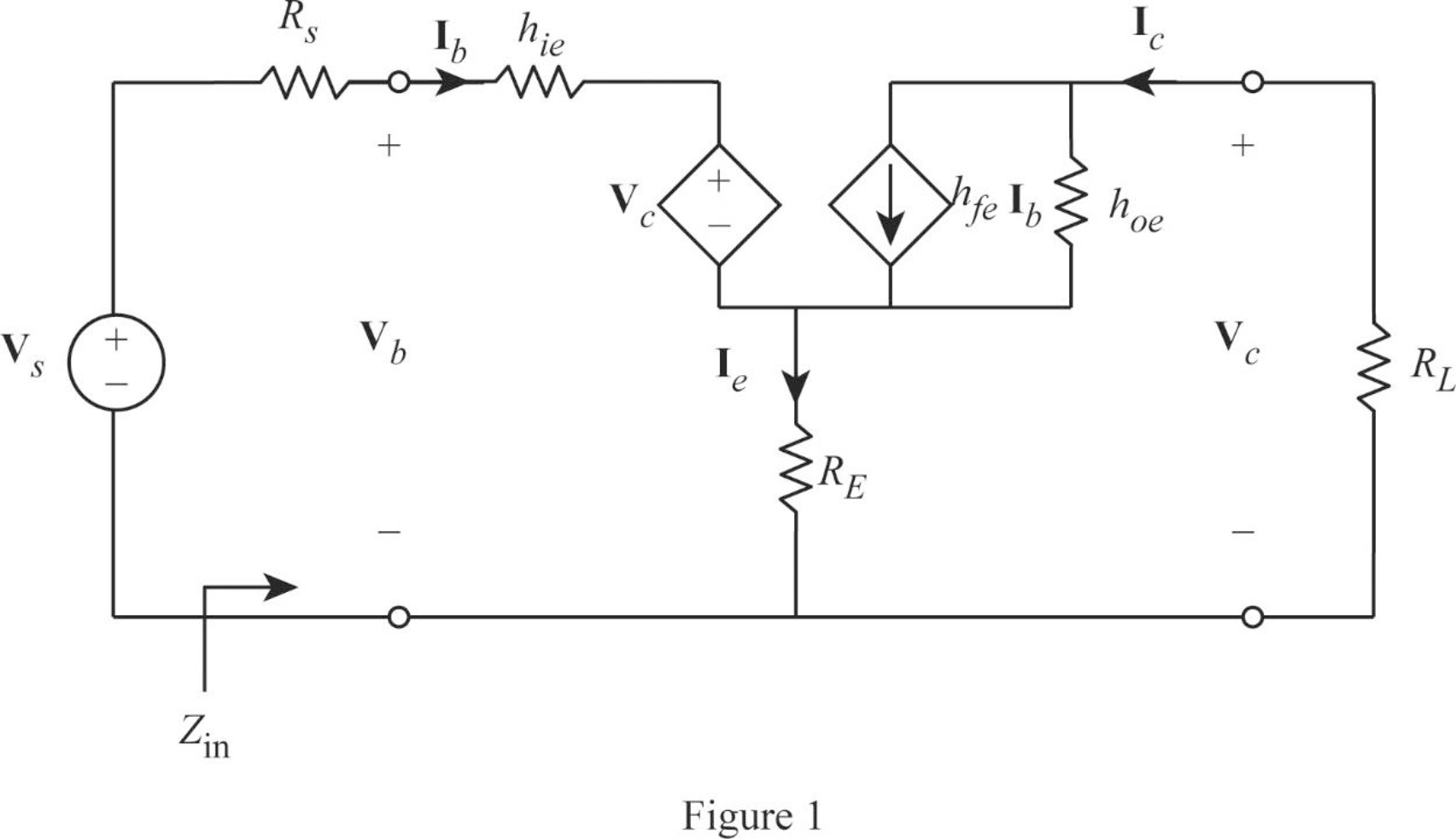
From Figure 1, write the expression for emitter current as follows:
Ie=Ib+Ic (4)
Write the expression for base voltage from the circuit in Figure 1 as follows:
Vb=hieIb+hreVc+(Ib+Ic)Re (5)
Write the expression for collector current as follows:
Ic=hfeIb+VcRe+1hoe (6)
Write the expression for collector voltage as follows:
Vc=−IcRL (7)
From Equation (7), substitute (−IcRL) for Vc in Equation (6) as follows:
Ic=hfeIb+(−IcRL)Re+1hoe(1+hoeRLRehoe+1)Ic=hfeIb
Rearrange the expression as follows:
IcIb=hfe1+hoeRLRehoe+1=hfe(1+Rehoe)1+Rehoe+hoeRL
IcIb=hfe(1+Rehoe)1+(Re+RL)hoe (8)
From Equation (2), substitute Ai for IcIb as follows:
Ai=hfe(1+Rehoe)1+(Re+RL)hoe
Substitute 150 for hfe, 10 μS for hoe, 200 Ω for Re, and 3.8 kΩ for RL as follows:
Ai=(150)[1+(200 Ω)(10 μS)]1+(200 Ω+3.8 kΩ)(10 μS)=(150)[1+(200 Ω)(10×10−6 S)]1+(200 Ω+3800 Ω)(10×10−6 S)=(150)(1.002)1.04=144.5192
Ai≅144.5
From Equation (6), substitute (hfeIb+VcRe+1hoe) for Ic in Equation (8) as follows:
hfeIb+VcRe+1hoeIb=hfe(1+Rehoe)1+(Re+RL)hoe
Rearrange the expression as follows:
hfeIb+VcRe+1hoe=hfe(1+Rehoe)1+(Re+RL)hoeIb[hfe(1+Rehoe)1+(Re+RL)hoe−hfe]Ib=VcRe+1hoe[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe1+(Re+RL)hoe]Ib=hoeVc1+Rehoe
Ib=[1+(Re+RL)hoe]hoeVc(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe] (9)
Rearrange the expression in Equation (5) as follows:
Vb=hieIb+hreVc+(IbRe+IcRe)
Vb=(hie+Re)Ib+hreVc+IcRe (10)
From Equations (7) and (9), substitute (−VcRL) for Ic and [1+(Re+RL)hoe]hoeVc(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe] for Ib as follows:
Vb=(hie+Re){[1+(Re+RL)hoe]hoeVc(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe]}+hreVc+(−VcRL)Re={(hie+Re)[1+(Re+RL)hoe]hoe(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe]+hre−ReRL}Vc
Rearrange the expression as follows:
VcVb=1{(hie+Re)[1+(Re+RL)hoe]hoe(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe]+hre−ReRL}
Substitute 150 for hfe, 2 kΩ for hie, (2.5×10−4) for hre, 10 μS for hoe, 200 Ω for Re, and 3.8 kΩ for RL as follows:
VcVb=1((2 kΩ+200 Ω)[1+(200 Ω+3.8 kΩ)(10 μS)](10 μS)[1+(200 Ω)(10 μS)]{(150)[1+(200 Ω)(10 μS)]−150−(200 Ω+3.8 kΩ)(10 μS)(150)}+(2.5×10−4)−200 Ω3.8 kΩ)=1((2000 Ω+200 Ω)[1+(200 Ω+3800 Ω)(10×10−6 S)](10×10−6 S)[1+(200 Ω)(10×10−6 S)]{(150)[1+(200 Ω)(10×10−6 S)]−150−(200 Ω+3800 Ω)(10×10−6 S)(150)}+(2.5×10−4)−200 Ω3800 Ω)=1{(2200 Ω)(1.04)(10×10−6 S)(1.002)[(150)(1.002)−150−6]+(2.5×10−4)−0.0526}=1{−0.004+(2.5×10−4)−0.0526}
Simplify the expression as follows:
VcVb=−17.7462≅−17.74
From Equation (1), substitute Av for VcVb to obtain the voltage gain of the transistor network.
Av=−17.74
From Equation (9), substitute (1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe][1+(Re+RL)hoe]hoeIb for Vc and from Equation (8), substitute hfe(1+Rehoe)1+(Re+RL)hoeIb for Ic in Equation (10) as follows:
Vb={(hie+Re)Ib+hre(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe][1+(Re+RL)hoe]hoeIb+hfe(1+Rehoe)1+(Re+RL)hoeIbRe}={(hie+Re)+hre(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe][1+(Re+RL)hoe]hoe+hfe(1+Rehoe)1+(Re+RL)hoeRe}Ib
Rearrange the expression as follows:
VbIb={(hie+Re)+hre(1+Rehoe)[hfe(1+Rehoe)−hfe−(Re+RL)hoehfe][1+(Re+RL)hoe]hoe+hfe(1+Rehoe)1+(Re+RL)hoeRe}
Substitute 150 for hfe, 2 kΩ for hie, (2.5×10−4) for hre, 10 μS for hoe, 200 Ω for Re, and 3.8 kΩ for RL as follows:
VbIb={(2 kΩ+200 Ω)+(2.5×10−4)[1+(200 Ω)(10 μS)][(150)(1+(200 Ω)(10 μS))−150−(200 Ω+3.8 kΩ)(10 μS)(150)][1+(200 Ω+3.8 kΩ)(10 μS)](10 μS)+(150)[1+(200 Ω)(10 μS)]1+(200 Ω+3.8 kΩ)(10 μS)(200 Ω)}=2200 Ω+(2.5×10−4)(1.002)(150.3−150−6)10.4 μS+(150.3)(200 Ω)1.04=2200 Ω−137.2933 Ω+28904 Ω=30967 ΩVbIb=30.967 kΩ≅31 kΩ
From Equation (3), substitute Zin for VbIb to obtain the input impedance of the transistor network.
Zin=31 kΩ
Consider output voltage (Vc) as 1 V and redraw the circuit in Figure 1 as Figure 2 to find the output impedance of the transistor network.
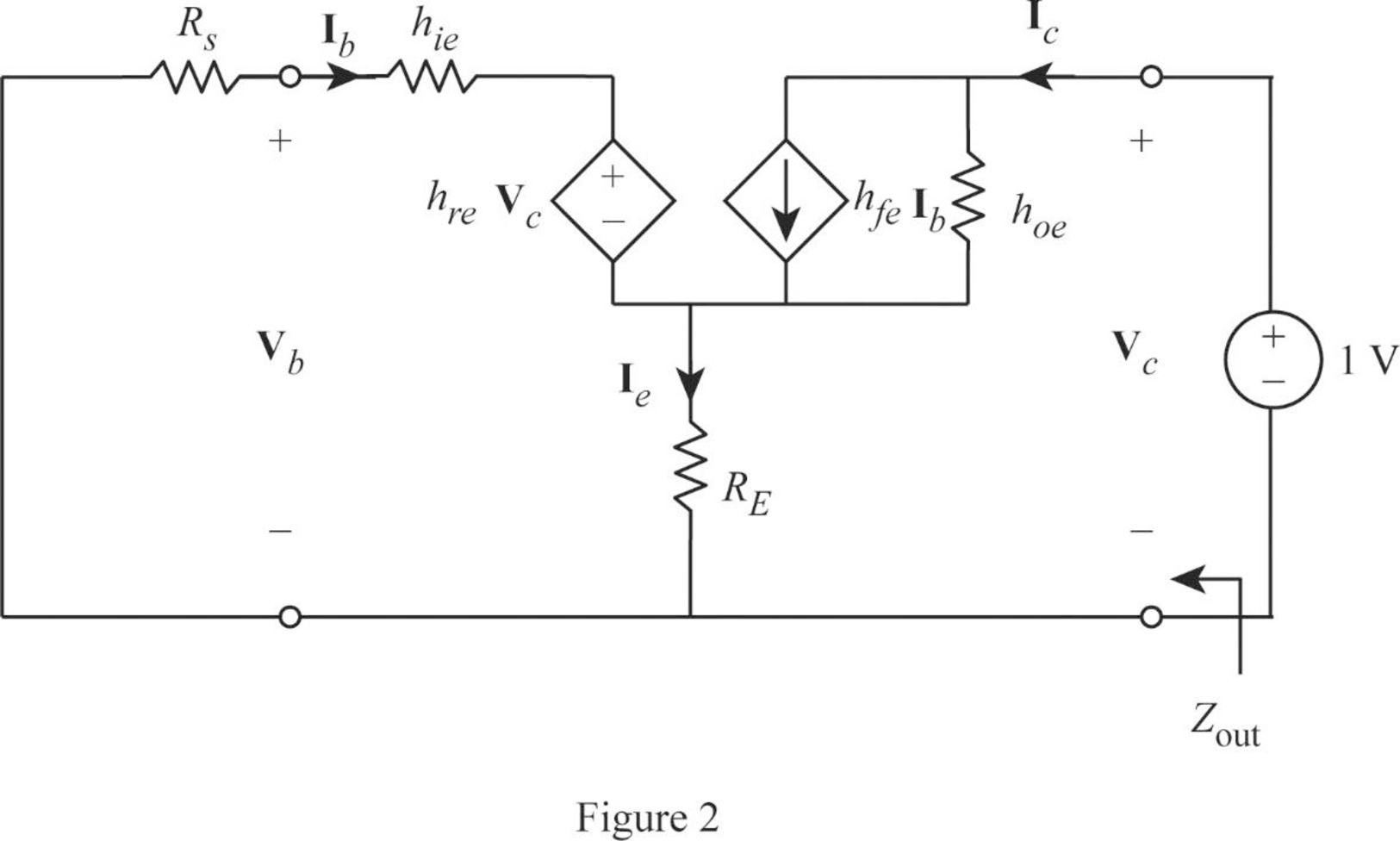
Apply KVL to the input loop for the circuit in Figure 2 as follows:
Ib(Rs+hie)+hreVc+Re(Ib+Ic)=0
Substitute 1 for Vc as follows:
Ib(Rs+hie)+hre+Re(Ib+Ic)=0
Ib(Rs+hie+Re)+hre+ReIc=0 (11)
Apply KCL at the output node for the circuit in Figure 2 as follows:
Ic=VcRe+1hoe+hfeIb=hoeVc1+hoeRe+hfeIb
Substitute 1 for Vc as follows:
Ic=hoe1+hoeRe+hfeIb
Rearrange the expression as follows:
Ic=hoe+(1+hoeRe)hfeIb1+hoeReIb=(1+hoeRe)Ic−hoe(1+hoeRe)hfe
Ib=Ichfe−hoe(1+hoeRe)hfe (12)
From Equation (12), substitute [Ichfe−hoe(1+hoeRe)hfe] for Ib in Equation (11) as follows:
[Ichfe−hoe(1+hoeRe)hfe](Rs+hie+Re)+hre+ReIc=0[(Rs+hie+Re)hfe+Re]Ic=(Rs+hie+Re)hoe(1+hoeRe)hfe−hre[(Rs+hie+Re)+hfeRehfe]Ic=(Rs+hie+Re)hoe−(1+hoeRe)hfehre(1+hoeRe)hfeIc=(Rs+hie+Re)hoe−(1+hoeRe)hfehre(1+hoeRe)(Rs+hie+Re)+hfeRe
Substitute 150 for hfe, 2 kΩ for hie, 1 kΩ for Rs, (2.5×10−4) for hre, 10 μS for hoe, 200 Ω for Re, and 3.8 kΩ for RL as follows:
Ic=(1 kΩ+2 kΩ+200 Ω)(10 μS)−[1+(10 μS)(200 Ω)](150)(2.5×10−4)[1+(10 μS)(200 Ω)](1 kΩ+2 kΩ+200 Ω)+(150)(200 Ω)=0.032−(1.002)(150)(2.5×10−4)(1.002)(3200 Ω)+30000 Ω=−0.005633206 Ω=−0.16864×10−6 S
Write the expression for output impedance of the transistor network as follows:
Zout=VcIc
Substitute 1 for Vc and (−0.16864×10−6 S) for Ic to obtain the output impedance of the transistor network.
Zout=1−0.16864×10−6 S=−5.9296×106 Ω=−5.9296 MΩ≅−6 MΩ
Conclusion:
Thus, the voltage gain, current gain, input impedance, and output impedance for the transistor network are −17.74_, 144.5_, 31 kΩ_, and −6 MΩ_, respectively.
