
Using supeerposition, determine the current through the inductance XL for the network of Fig. 19.105.
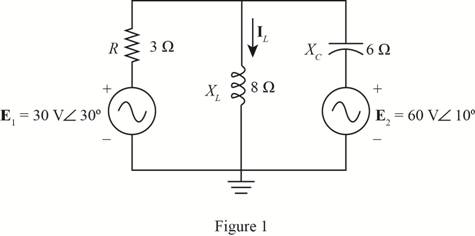
The current flowing through the inductance
Answer to Problem 1P
The current through the inductor is
Explanation of Solution
Given:
The given circuit is shown in Figure 1.

Calculation:
To apply superposition theorem, first consider the effect of voltage source
The required diagram is shown in Figure 2.
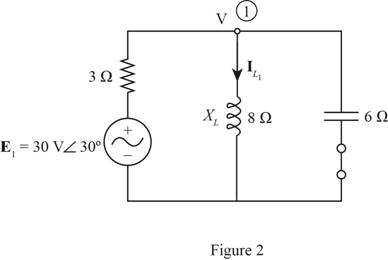
Let the voltage at node 1 is
The current through the inductor is given by
Substitute
Now consider the effect of source voltage
The required diagram is shown in Figure 3.
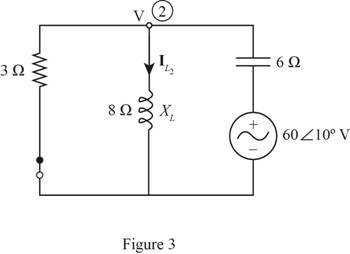
Apply the KCL at node 2.
The current through the inductor is given by,
Therefore, according to super position theorem the current through the inductor is given by
Substitute
Conclusion:
Therefore, the current through the inductor is
Want to see more full solutions like this?
Chapter 19 Solutions
Introductory Circuit Analysis; Laboratory Manual For Introductory Circuit Analysis Format: Kit/package/shrinkwrap
- NO AI PLEASE SHOW WORKarrow_forwardConsider a Continuous- time LTI System. described by y' (+)+ nycH) = x(+) find yet for усн b) x(+) = u(+) Sul. a) x(+)= ētu(+). c) X(+= √(+) jw few) +2 kW) = X (w) (jw+2) Y(W)= X(w) Han Youn X(w) ½ztjuk a) X (W) = 1 + jw Y(W)= X(w) H(W). I tjw z+jw tjw = 1+jw 2+jw y (+) = (e+ - e²+) 4(+) b) XIW): π (W) + |/|/w Y₁W) = [π √(W) + 1/w] =² + j w zxjw How = π √(w) 1 ㅠ беш) 24jw + *= II 8 (W) + 1 1 1 1 2 4 jw = 2 y(+)= \uct) - e²+us+] - SINAALINE ju 2+ jwarrow_forwardNO AI PLEASE SHOW WORKarrow_forward
- Don't use ai to answer I will report you answerarrow_forwardCompute the Laplace transform of the following time domain function using only L.T. properties: f(t)=(t-3)eu(t-2) The Laplace Transform of x(t) = 8(-1) - u(1) is X(s): = (a) 2πδ(s) (b) 1-1 S (c) j2πδ (s) (d) - 1/3 Sarrow_forwardUf you don't know, don't attempt this questions,no Ai or it's screen shot should be usedarrow_forward
- Find the initial and final values of sequence x(n) from X(Z) below using the initial and final value properties X(Z) = = z-1arrow_forwardOnly expert should attempt,no Ai or screen shot it solving, I need solution s to all of themarrow_forwardDon't use ai to answer I will report you answerarrow_forward
- Find the autocorrelation function of the periodic function x(t) 1 0 1 2 3 tarrow_forwardFind Laplace transform for x(t) = e−³t √∞ (1 − t) sin(t − 2) §(t)dt Find Laplace transform and the corresponding ROC for x(t) = e˜³τsin(2t) u(t)dtarrow_forwardfind the inverse Laplace transform of X(s)=- s+5 (s-1)(s-2)(s-3) i) Re[s]> 3 ii) Re[s]<1 iii) 1arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
