
Concept explainers
A 4-lb uniform rod is supported by a pin at O and a spring at A and is connected to a dashpot at B. Determine (a) the differential equation of motion for small oscillations, (b) the angle that the rod will form with the horizontal 5 s after end B has been pushed 0.9 in. down and released.
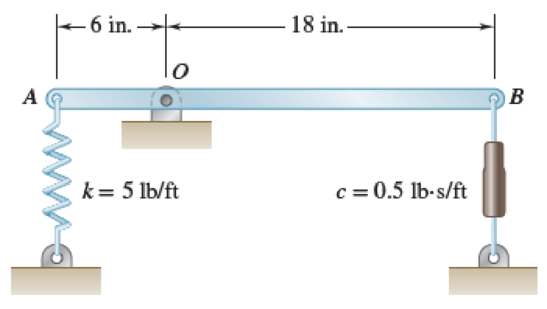
Fig. P19.165
(a)
The differential equation of motion for small oscillations.
Answer to Problem 19.165RP
The differential equation of motion for small oscillations is
Explanation of Solution
Given information:
The weight of the uniform rod (W) is 4 lb.
The distance between A to O (a) is 6 inch.
The distance between O to B (b) is 18 in.
The spring constant (k) is 5 lb/ft.
The damping coefficient (c) is
The acceleration due to gravity (g) is
Calculation:
Calculate the mass of the uniform rod (m) using the formula:
Substitute 4 lb for W and
Show the free body diagram of the rod as Figure (1).
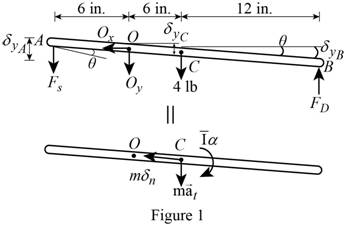
For small angle, take
Calculate the deflection at the point A
Substitute 6 in. for a.
Calculate the deflection at the point B
Substitute 18 in. for b.
Calculate the deflection at the point C
Substitute 6 in. for a.
Take the moment about O.
Calculate for the spring force
Substitute
Calculate the damping force
Substitute
Calculate the moment of inertia
Substitute 6 in. for a and 18 in. for b.
The angle
Calculate the acceleration
Substitute 6 in. for a and
Substitute
Consider equilibrium.
Take the moment about O.
Substitute 2 for
Substitute
Therefore, the differential equation of motion for small oscillations is
(b)
The angle that the rod
Answer to Problem 19.165RP
The angle that the rod
Explanation of Solution
Given information:
The weight of the uniform rod (W) is 4 lb.
The distance between A to O (a) is 6 inch.
The distance between O to B (b) is 18 inch.
The spring constant (k) is 5 lb/ft.
The damping coefficient (c) is
The acceleration due to gravity (g) is
Calculation:
Consider the equation (3).
Substitute
Solve the above equation.
Since the computed roots are real and distinct.
Write the expression for the general solution for the differential equation as follows:
Substitute 0 for t.
Differentiate the equation (4) with respect to time ‘t’.
Substitute 0 for t.
The above solution corresponds to a no vibratory motion because the roots
Therefore, the angle that the rod
Want to see more full solutions like this?
Chapter 19 Solutions
<LCPO> VECTOR MECH,STAT+DYNAMICS
- The members of a truss are connected to the gusset plate as shown in (Figure 1). The forces are concurrent at point O. Take = 90° and T₁ = 7.5 kN. Part A Determine the magnitude of F for equilibrium. Express your answer to three significant figures and include the appropriate units. F= 7.03 Submit ? kN Previous Answers Request Answer × Incorrect; Try Again; 21 attempts remaining ▾ Part B Determine the magnitude of T2 for equilibrium. Express your answer to three significant figures and include the appropriate units. Figure T₂ = 7.03 C T2 |? KN Submit Previous Answers Request Answer × Incorrect; Try Again; 23 attempts remaining Provide Feedbackarrow_forwardConsider the following acid-base reaction: Fe3+(aq) +3H2O -Fe(OH)3 (s) + 3H* ← A. Using thermodynamics, calculate the equilibrium constant K at 25°C (The AG° of formation of Fe(OH)3(s) is -699 kJ/mol). B. Using the value of K you calculated in part a, if a solution contains 10-4 M Fe3+ and has a pH of 7.5, will Fe(OH)3(s) precipitate? Show all calculations necessary to justify your answer. Note that the reaction as written is for precipitation, not dissolution like Ksp-arrow_forwardA vertical force of F = 3.4 kN is applied to the hook at A as shown in. Set d = 1 m. Part A 3 m 3m 0.75 m 1.5 m. Determine the tension in cable AB for equilibrium. Express your answer to three significant figures and include the appropriate units. FAB= Value Submit Request Answer Part B Units ? Determine the tension in cable AC for equilibrium. Express your answer to three significant figures and include the appropriate units. FAC = Value Submit Request Answer Part C ? Units Determine the tension in cable AD for equilibrium. Express your answer to three significant figures and include the appropriate units.arrow_forward
- Consider the heat engine operating at steady state between the two thermal reservoirs shown at the right while producing a net power output of 700 kW. If 1000 kW of heat (Q̇H) is transferred to the heat engine from a thermal reservoir at a temperature of TH = 900 K, and heat is rejected to a thermal reservoir at a temperature of TL = 300 K, is this heat engine possible? Can you answer this question for me and show all of the workarrow_forward1.12 A disk of constant radius r is attached to a telescoping rod that is extending at a constant rate as shown in Fig. P1.12. Both the disk and the rod are rotating at a constant rate. Find the inertial velocity and acceleration of point P at the rim of the disk. ท2 L 0 SS P α e 0 O' êL Fig. P1.12 Rotating disk attached to telescoping rod. 60 LLarrow_forwardTwo different options A and B with brake pads for disc brakes are connected to the rope drum. The diameter of the rope drum is 150 mm. What distance must the pads B be at from the center of rotation to cover the same distance as A?A B- Width 50 mm - Width 60 mm- Evidence center 120mm - Construction power 900 N from rotation center.- Maintains a weight of 200 kgwhen the installation force is 1.4kN (μ is missing from the data)M=μF(Ry-Ri)Right answer R=187 mmarrow_forward
- Assume the xy plane is level ground, and that the vertical pole shown in the diagram lies along the z-axis with its base at the origin. If the pole is 5 m tall, and a rope is used to pull on the top of the pole with a force of 400 N as shown, determine the magnitudes of the parallel and perpendicular components of the force vector with respect to the axis of the post i.e. with respect to the z-axis.arrow_forward4-1 Q4: Q5: (20 Marks) Find √48 using False Position Method with three iterations. Hint: the root lies between 3 and 4. (20 Marks)arrow_forwardDetermine the angle between vectors FA and FB that is less than 180 degrees. FA is the vector drawn from the origin to point A (-4, 4, 2) while FB is the vector drawn from the origin to point B (3, 1, -3).arrow_forward
- Find the resultant force vector from adding F1, F2 and F3, where … F1 = {-8i+10j-32k} N F2 is 40 N in magnitude with coordinate direction angles α, β, and γ, of 45, 120 and 60 degrees, respectively and F3 is 22 N in magnitude with transverse and azimuth angles of 65 and 40 degrees, respectively Express your final answer as a Cartesian vector as well as a magnitude with angles.arrow_forwardA 2-kW resistance heater wire with thermal conductivity of k=20 W/mK, a diameter of D=4mm, and a length of L=0.9m is used to boil water. If the outer surface temp of the resistance wire is Ts=110 degrees C, determine the temp at the center of the wire.arrow_forwardA flat-plate solar collector is used to heat water by having water flow through tubes attached at the back of the thin solar absorber plate. The absorber plate has emmisssivity and an absorptivity of 0.9. The top surface where x=0 temp of the absorber is T0=35 degrees C, and solar radiation is incident on the basorber at 500 W/m^2 with a surrounding temp of 0 degrees C. The convection heat transfer coefficient at the absorber surface is 5 W/m^2 K, while the ambient temp is 25 degrees C. Show that the variation of the temp in the basorber plate can be expressed as T(x)=-(q0/k)x+T0, and determine net heat flux, q, absorbed by solar collector.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





