
Concept explainers
(a)
The frequency
(a)
Answer to Problem 19.14P
The frequency
Explanation of Solution
Given Information:
The mass
The mass
The spring constant (k) is
The value of acceleration due to gravity (g) is
Calculation:
Show the electromagnet with cable and crane arrangement as in Figure (1).
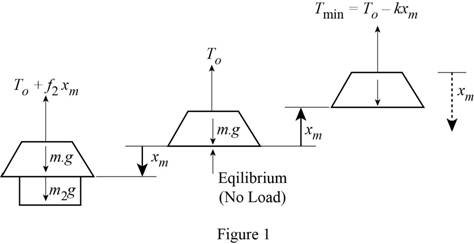
Refer Figure (1), when the electromagnet is off, the tension in the cable is equal to the force due to the mass of the electromagnet.
Express the force balance equation for the first case.
Here,
Calculate the natural circular frequency
Substitute
Calculate the natural frequency
Substitute
By referring the Figure 1, when the electromagnet is on, the tension in the cable is equal to the force due to the mass of the electromagnet and that due to mass of the scrap steel.
Express the force balance equation for the second case.
Here,
Substitute Equation (1) in Equation (2).
Calculate the amplitude
Substitute
Calculate the maximum velocity
Substitute
Therefore, the frequency
(b)
The minimum tension
(b)
Answer to Problem 19.14P
The minimum tension
Explanation of Solution
Given Information:
The mass
The mass
The spring constant (k) is
The value of acceleration due to gravity (g) is
Calculation:
The minimum value of tension occurs when the displacement (x) is maximum at upward direction
Express the minimum tension
Substitute Equations (1) and (3) in Equation (4).
Calculate the minimum tension
Substitute 150 kg for
Therefore, the minimum tension
(c)
The velocity
(c)
Answer to Problem 19.14P
The velocity
Explanation of Solution
Given Information:
The mass
The mass
The spring constant (k) is
The value of acceleration due to gravity (g) is
Calculation:
Express the displacement (x) of the simple harmonic motion at any instant.
Here,
When time (t) is 0, the initial displacement is
Substitute 0 for t and
For the above equation to satisfy the value of
Calculate the velocity
Substitute
Therefore, the velocity
Want to see more full solutions like this?
Chapter 19 Solutions
<LCPO> VECTOR MECH,STAT+DYNAMICS
- Problem 2 (40 Points) A particle of mass m is embedded at a distance a from the center of a massless circular disk of radius r. The disk rolls without slipping down a plane inclined at an angle a with the horizontal. A horizontal force of Ễ = −Fxî + Fyĵ resists motion of the disk down the plane by pushing on the disk at the axle that runs through the center of the disk. a) Find the kinetic energy T. (10 points) b) Find the potential energy V. (10 points) c) Write a position vector to the axle at the center of the wheel in terms of x and y. (10 points) d) Using virtual work, find the applied force Q₁ that would go in Lagrange's Equations. DO NOT WRITE OUT OR SOLVE LAGRANGES'S EQUATIONS. (10 points) x r m e 10 g F α HINTS 1) Consider using the STATIONARY red xy frame a reference frame from which to draw vectors 2) The red xy system DOES NOT move. It is stationary. 3) Consider that the disk rolls a distance of re down the ramparrow_forwardDraw a counter balance circuit of a vertical cylinder. using counter balance valve and external load.arrow_forwardplease sketch a stress-strain diagram for a typical structural steel in tension and display all of the important features.arrow_forward
- Problem 1 (30 Points) Consider the following 2 scenarios. In scenario 1, a mass m slides on a cylindrical surface of radius R. In scenario 2, a mass m hangs at the end of a thin massless rod of length R. In both scenarios, there is no friction either on the surface (scenario 1), or at the pivot point of the pendulum (scenario 2). Also in both scenarios, there is one generalized coordinate, . R Scenario 1 R m R g Scenario 2 m HINT: In both scenarios, it is much easier to choose your datum for potential energy as the center of the bowl (scenario 1), or the pivot point of the pendulum (scenario 2). Part I a) Determine the Lagrangian for each system. DO NOT FIND THE EQUATIONS OF MOTION (5 points) b) What can you say about the systems based on the Lagrangian? (2 points) c) Solve for the equations of motion for both systems. (8 points) Part II Now, for scenario 1, introduce an additional coordinate and treat it as a nonholonomic system to determine the normal force acting on the mass. a)…arrow_forwardConsider 0.65 kg of N2 at 300 K, 1 bar contained in a rigid tank connected by a valve to another rigid tank holding 0.3 kg of CO2 at 300 K, 1 bar. The valve is opened and gases are allowed to mix, achieving an equilibrium state at 290 K. Determine: (a) the volume of each tank, in m³. (b) the final pressure, in bar. (c) the magnitude of the heat transfer to or from the gases during the process, in kJ. (d) the entropy change of each gas and of the overall system, in kJ/K.arrow_forward(Read Image) (Answer: ω = 1.10 rad/sec CW)arrow_forward
- What is the configuration of the control loop if steam must be shut down in case of a problem? (I found this question on the internet and was wondering what the answer is) A.Valve is fail open, PIC is direct-acting, TIC is reverse acting, and controller algorithm is feed-forwarding.B. Valve is fail open, PIC is reverse-acting, TIC is direct acting, and controller algorithm is cascade.C. Valve is fail closed, PIC is direct-acting, TIC is reverse acting, and controller algorithm is feed-forward.D. Valve is fail closed, PIC is reverse-acting, TIC is reverse acting, and controller algorithm is cascade.arrow_forwardWhat is the procedure to replace the input bellows?(I found this question on the internet and was wondering what the correct answer is out of interest) Remove tubing, old bellows and flapper assembly, install new bellows, connect tubing, install flapper assembly, then calibrate the positioner.Remove tubing, old bellows and cam, install new bellows, connect tubing, install cam, then calibrate the positioner.C. Remove tubing and old bellows, align the quadrant beam, install new bellows and connect tubing, then calibrate the positioner.D. Remove tubing and old bellows, install new bellows and connect tubing, align the quadrant beam, then calibrate the positioner.arrow_forwardGiven the following information: (I found this question on the internet and was wondering what the correct answer is) Firing rate demand = 20% Fuel air ratio = 2:1 Fuel flow = 20% Minimum air flow setting = 5% What is the set point for the air flow controller? 5%B. 10%C. 25%D. 40%arrow_forward
- . Where is a dew point analyzer installed to measure instrument air?(I found this question on the internet and am wondering what the correct answer is) A. AB. BC. CD. Darrow_forwardThe piston at the bottom of the stroke is 0% open. Which adjustment will change the zero setting to 5% open? ( I found this sample question on the internet and was wondering what the correct answer is out of interest) A.Slide component 2 towards the pivotB. Slide component 2 away from the pivot.C. Increase spring tension using adjustment 1.D. Decrease spring tension using adjustment 1.arrow_forward(read image) (Answer: vA = 4.57 ft/sec)arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





