
The precession axis, rates of precession, and the spin rate of the satellite after the impact.
Answer to Problem 18.129P
The precession along x, y, and z axis
The precession rate
The spin rate
Explanation of Solution
Given information:
The weight of geostationary satellite (W) is 800 lb.
The angular velocity of the satellite
The weight of a meteorite
The travelling velocity of the meteorite
The distance value b is 20 in..
The radii of gyration of the satellite along x, y, and z direction (
Calculation:
Determine the mass of the satellite (m).
Here, g is the acceleration due to gravity.
Substitute 800 lb for W and
Determine the principal moment of inertia along x axis.
Substitute
Determine the principal moment of inertia along y axis.
Substitute
Determine the principal moment of inertia along z axis.
Substitute
Determine the mass of the meteorite
Substitute 6 oz for
Determine the initial moment of meteorite
Substitute
Consider that the position of the satellite mass center plus the meteorite is essentially that of the satellite alone.
Determine the position of the point B relative to the mass center.
Here, x is the horizontal distance and y is the vertical distance.
Substitute 42 in. for x and 20 in. for y.
The angular velocity of satellite before impact
The angular velocity of satellite before impact along x, y, and z axis is
Determine the angular momentum of satellite–meteorite system before impact
Substitute
Principle of impulse and momentum for satellite–meteorite system:
The value of moments about G is
The expression for
Determine the angular velocity about x axis.
Substitute
Determine the angular velocity about y axis.
Substitute
Determine the angular velocity about z axis.
Substitute
Determine the vector format of angular velocity using the relation;
Substitute
Determine the magnitude of the angular velocity
Substitute
Determine the magnitude of angular momentum
Substitute
Motion after impact:
The moment of inertia about x and y axis is equal, the body moves as an axisymmetrical body with the y axis as the symmetry axis.
The moment of inertia about the symmetry axis is
The moment of inertia about a transverse axis through G is
The precession is retrograde when the value of
Determine the angle
Substitute
Determine the angle
Substitute
Determine the angle
Substitute
Thus, the precession along x, y, and z axis
The angle
Determine the angle
Substitute
Determine the value of
Substitute
Draw the free body diagram of precession and spin axis as in Figure (1).
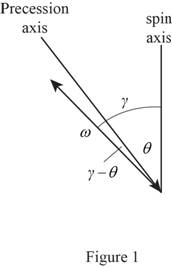
Draw the free body diagram of triangle of vector addition as in Figure (2).
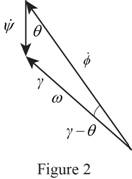
Write the relation between the angles using the sine law.
Determine the precession rate
Substitute
Therefore, the precession rate
Determine the rate of spin
Substitute
The precession is retrograde due to value of
Therefore, the spin rate
Want to see more full solutions like this?
Chapter 18 Solutions
VECTOR MECHANICS FOR ENGINEERS W/CON >B
- One end of a thin uniform rod of mass m and length 31 rests against a smooth vertical wall. The other end of the rod is attached by a string of length 1 to a fixed point O which is located a distance 21 from the wall. A horizontal force of magnitude F₁ is applied to the lower end of the rod as shown. Assuming the rod and the string remain in the same vertical plane perpendicular to the wall, find the angle 0 between the rod and the wall at the position of static equilibrium. Notes: This quiz is going to walk you through a sequence of steps to do this. It won't give you the answers, but it will hopefully get you to see how to approach problems like this so that you have a working reference/template in the future. This is actually a modified version of a problem from the textbook (6.3). Note that in that problem, is not actually given. It has been introduced for convenience as we move through solving the problem, and should not show up in the final answer. DO NOT DO PROBLEM 6.3. It is…arrow_forwardvarrow_forward13.64 The shaft shown in Sketch h transfers power between the two pulleys. The tension on the slack side (right pul- ley) is 30% of that on the tight side. The shaft rotates at 900 rpm and is supported uniformly by a radial ball bearing at points 0 and B. Select a pair of radial ball bear- ings with 99% reliability and 40,000 hr of life. Assume Eq. (13.83) can be used to account for lubricant clean- liness. All length dimensions are in millimeters. Ans. Cmin = 42,400 N.arrow_forward
- A 4 inch wide, 12 inch tall cross section beam is subjected to an internal shear of 5.5 kips. What is the maximum transverse shear stress in the beam in psi if this bending is about the x axis?arrow_forwardA Brayton cycle produces 14 MW with an inlet state of 17°C, 100 kPa, and a compression ratio of 16:1. The heat added in the combustion is 960 kJ/kg. 0.7 MW of heat transferred from the turbine to the environment. What are the highest temperature and the mass flow rate of air? Assume cold air properties.arrow_forward. A gas turbine with air enters the compressor at 300 K, 1 bar, and exits from the turbine at 750 K, 1 bar. The thermal efficiency of the cycle is 40.1% and the back work ratio (BWR) is 0.4. Find the pressure ratio of the cycle. Assume variable specific heat.arrow_forward
- A regenerative gas turbine power plant is shown in Fig. below. Air enters the compressor at 1 bar, 27°C with a mass flow rate of 0.562 kg/s and is compressed to 4 bar. The isentropic efficiency of the compressor is 80%, and the regenerator effectiveness is 90%. All the power developed by the high-pressure turbine is used to run the compressor. The low-pressure turbine provides the net power output. Each turbine has an isentropic efficiency of 87% and the temperature at the inlet to the highpressure turbine is 1200 K. Assume cold air properties, determine: a. The net power output, in kW. b. The thermal efficiency of the cycle.arrow_forwardFor tixed inlet state and exit pressure, use a cold-air standard analysis to show that the pressure ratio across the two compressor stages that gives nunimum work input is:=)) k/(k-1) when Ta Ti, where Ta is the temperature of the air entering the second stage compressor and Pi is the intercooler pressure. Put the suitable assumptionsarrow_forwardDerive the equation below ah ap ax 12μ ax, +( ah ap ay 12μ ay Where P P (x, y) is the oil film pressure. 1..ah 2 axarrow_forward
- Can you determine the eignevalues by hand?arrow_forwardMonthly exam 13 2021-2022 Power plant Time: 1.5 Hrs Q1. A The gas-turbine cycle shown in Fig. is used as an automotive engine. In the first turbine, the gas expands to pressure Ps, just low enough for this turbine to drive the compressor. The gas is then expanded through the second turbine connected to the drive wheels. The data for the engine are shown in the figure, and assume that all processes are ideal. Determine the intermediate pressure Ps, the net specific work output of the engine, and the mass flow rate through the engine. Find also the air temperature entering the burner T3 and the thermal efficiency of the engine. Exhaust Air intake Φ www Regenerator www Bumer Compressor Turbine Power turbine et 150 kW Wompressor P₁ = 100 kPa T₁ = 300 K PP₁ =60 P-100 kPa T₁ = 1600 K Q2. On the basis of a cold air-standard analysis, show that the thermal efficiency of an ideal regenerative gas turbine can be expressed as 77 = 1- where - () () гp is the compressor pressure ratio, and T₁ and…arrow_forwardI need to find m in R = mD from the image given. Do you really need to know what R and D is to find R. I was thinking geometrically we can find a relationship between R and D. D = R*cos(30). Then R = mD becomes m = R/D = 1/cos(30) = 1.1547. Is that correct?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





