
The precession axis, rates of precession, and the spin rate of the satellite after the impact.
Answer to Problem 18.129P
The precession along x, y, and z axis
The precession rate
The spin rate
Explanation of Solution
Given information:
The weight of geostationary satellite (W) is 800 lb.
The angular velocity of the satellite
The weight of a meteorite
The travelling velocity of the meteorite
The distance value b is 20 in..
The radii of gyration of the satellite along x, y, and z direction (
Calculation:
Determine the mass of the satellite (m).
Here, g is the acceleration due to gravity.
Substitute 800 lb for W and
Determine the principal moment of inertia along x axis.
Substitute
Determine the principal moment of inertia along y axis.
Substitute
Determine the principal moment of inertia along z axis.
Substitute
Determine the mass of the meteorite
Substitute 6 oz for
Determine the initial moment of meteorite
Substitute
Consider that the position of the satellite mass center plus the meteorite is essentially that of the satellite alone.
Determine the position of the point B relative to the mass center.
Here, x is the horizontal distance and y is the vertical distance.
Substitute 42 in. for x and 20 in. for y.
The angular velocity of satellite before impact
The angular velocity of satellite before impact along x, y, and z axis is
Determine the angular momentum of satellite–meteorite system before impact
Substitute
Principle of impulse and momentum for satellite–meteorite system:
The value of moments about G is
The expression for
Determine the angular velocity about x axis.
Substitute
Determine the angular velocity about y axis.
Substitute
Determine the angular velocity about z axis.
Substitute
Determine the vector format of angular velocity using the relation;
Substitute
Determine the magnitude of the angular velocity
Substitute
Determine the magnitude of angular momentum
Substitute
Motion after impact:
The moment of inertia about x and y axis is equal, the body moves as an axisymmetrical body with the y axis as the symmetry axis.
The moment of inertia about the symmetry axis is
The moment of inertia about a transverse axis through G is
The precession is retrograde when the value of
Determine the angle
Substitute
Determine the angle
Substitute
Determine the angle
Substitute
Thus, the precession along x, y, and z axis
The angle
Determine the angle
Substitute
Determine the value of
Substitute
Draw the free body diagram of precession and spin axis as in Figure (1).
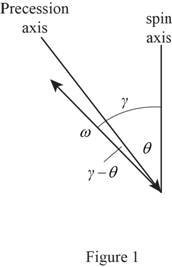
Draw the free body diagram of triangle of vector addition as in Figure (2).

Write the relation between the angles using the sine law.
Determine the precession rate
Substitute
Therefore, the precession rate
Determine the rate of spin
Substitute
The precession is retrograde due to value of
Therefore, the spin rate
Want to see more full solutions like this?
Chapter 18 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
- CORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I REALLY NEED FBD. The roof truss shown carries roof loads, where P = 10 kN. The truss is consisting of circular arcs top andbottom chords with radii R + h and R, respectively.Given: h = 1.2 m, R = 10 m, s = 2 m.Allowable member stresses:Tension = 250 MPaCompression = 180 MPa1. If member KL has square section, determine the minimum dimension (mm).2. If member KL has circular section, determine the minimum diameter (mm).3. If member GH has circular section, determine the minimum diameter (mm).ANSWERS: (1) 31.73 mm; (2) 35.81 mm; (3) 18.49 mmarrow_forwardPROBLEM 3.23 3.23 Under normal operating condi- tions a motor exerts a torque of magnitude TF at F. The shafts are made of a steel for which the allowable shearing stress is 82 MPa and have diameters of dCDE=24 mm and dFGH = 20 mm. Knowing that rp = 165 mm and rg114 mm, deter- mine the largest torque TF which may be exerted at F. TF F rG- rp B CH TE Earrow_forward1. (16%) (a) If a ductile material fails under pure torsion, please explain the failure mode and describe the observed plane of failure. (b) Suppose a prismatic beam is subjected to equal and opposite couples as shown in Fig. 1. Please sketch the deformation and the stress distribution of the cross section. M M Fig. 1 (c) Describe the definition of the neutral axis. (d) Describe the definition of the modular ratio.arrow_forward
- using the theorem of three moments, find all the moments, I only need concise calculations with minimal explanations. The correct answers are provided at the bottomarrow_forwardMechanics of materialsarrow_forwardusing the theorem of three moments, find all the moments, I need concise calculations onlyarrow_forward
- Can you provide steps and an explaination on how the height value to calculate the Pressure at point B is (-5-3.5) and the solution is 86.4kPa.arrow_forwardPROBLEM 3.46 The solid cylindrical rod BC of length L = 600 mm is attached to the rigid lever AB of length a = 380 mm and to the support at C. When a 500 N force P is applied at A, design specifications require that the displacement of A not exceed 25 mm when a 500 N force P is applied at A For the material indicated determine the required diameter of the rod. Aluminium: Tall = 65 MPa, G = 27 GPa. Aarrow_forwardFind the equivalent mass of the rocker arm assembly with respect to the x coordinate. k₁ mi m2 k₁arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





