
Concept explainers
A standing wave is described by the wave function
where x and y are in meters and t is in seconds. (a) Prepare graphs showing y as a function of x for five instants: t = 0, 5 ms, 10 ms, 15 ms, and 20 ms. (b) From the graph, identify the wavelength of the wave and explain how to do so. (c) From the graph, identify the frequency of the wave and explain how to do so. (d) From the equation, directly identify the wavelength of the wave and explain bow to do so. (e) From the equation, directly identify the frequency and explain how to do so.
(a)
To draw: The graphs showing
Answer to Problem 18.18P
The graph of
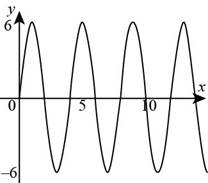
Figure (1)
The graph of
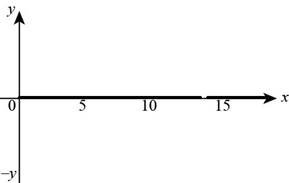
Figure (2)
The graph of
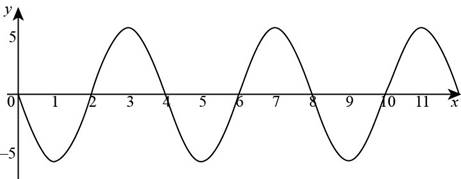
Figure (3)
The graph of
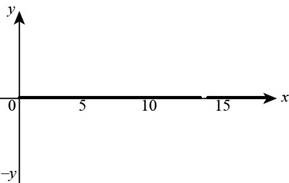
Figure (4)
The graph of

Figure (5)
Explanation of Solution
Introduction:
The values of
Explanation:
Given info: The sinusoidal waves function is,
For
Substitute
The graph of
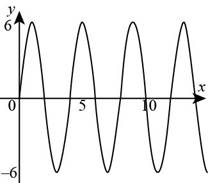
Figure (1)
For
Substitute
The graph of

Figure (2)
For
Substitute
The graph of
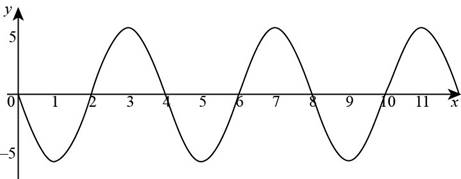
Figure (3)
For
Substitute
The graph of

Figure (4)
For
Substitute
The graph of
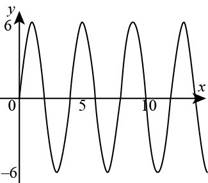
Figure (5)
(b)
Answer to Problem 18.18P
Explanation of Solution
Given info: The sinusoidal waves function is
The distance between the two-crest point or two trough point is called the wavelength of the wave.
From the figure (1), the distance between the two crest point is
Conclusion:
Therefore, the wavelength of the wave is
(c)
Answer to Problem 18.18P
Explanation of Solution
Given info: The sinusoidal waves function is
Compare the equation (1) with
The frequency of the wave is,
Substitute
Conclusion:
Therefore, the frequency of the wave is
(d)
Answer to Problem 18.18P
Explanation of Solution
Given info: The sinusoidal waves function is
Compare the equation (1) with
The frequency of the wave is,
Substitute
Conclusion:
Therefore, the wavelength of the wave is
(e)
Answer to Problem 18.18P
Explanation of Solution
Given info: The sinusoidal waves function is
Compare the equation (1) with
The frequency of the wave is,
Substitute
Conclusion:
Therefore, the frequency of the wave is
Want to see more full solutions like this?
Chapter 18 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- A force acting on a particle moving in the xy plane is given by F = (2yî + x²), where F is in newtons and x and y are in meters. The particle moves from the origin to a final position having coordinates x = 5.60 m and y = 5.60 m, as shown in the figure below. y (m) B (x, y) x (m) (a) Calculate the work done by F on the particle as it moves along the purple path (0 Ⓐ©). ] (b) Calculate the work done by ♬ on the particle as it moves along the red path (0 BC). J (c) Is F conservative or nonconservative? ○ conservative nonconservativearrow_forwardA 3.5-kg block is pushed 2.9 m up a vertical wall with constant speed by a constant force of magnitude F applied at an angle of 0 = 30° with the horizontal, as shown in the figure below. If the coefficient of kinetic friction between block and wall is 0.30, determine the following. (a) the work done by F J (b) the work done by the force of gravity ] (c) the work done by the normal force between block and wall J (d) By how much does the gravitational potential energy increase during the block's motion? ]arrow_forwardPhysics different from a sea breeze from a land breezearrow_forward
- File Preview Design a capacitor for a special purpose. After graduating from medical school you and a friend take a three hour cruise to celebrate and end up stranded on an island. While looking for food, a spider falls on your friend giving them a heart attack. Recalling your physics, you realize you can build a make-shift defibrillator by constructing a capacitor from materials on the boat and charging it using the boat's battery. You know that the capacitor must hold 100 J of energy and be at 1000 V (fortunately this is an electric boat which has batteries that are 1000 V) to work. You decide to construct the capacitor by tightly sandwiching a single layer of Saran wrap between sheets of aluminum foil. You read the Saran wrap box and fortunately they tell you that it has a thickness 0.01 mm and dielectric constant of 2.3. The Saran wrap and foil are 40 cm wide and very long. How long is the final capacitor you build that saves your friend?arrow_forwardHow do I plot the force F in Matlba (of gravity pulling on the masses) versus spring displacement, and fit the data with a linear function to find the value for the spring constant. To get a linear fit, use polynomial order 1. Report the value of 'k' from the fit. What code is used?arrow_forwardOk im confused on this portion of the questions being asked. the first snip is the solution you gave which is correct. BUt now it is asking for this and im confused. The magnitude of the force F_11 is __________LB. The direction of the force F_11 is __________LB.arrow_forward
- Solve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardThe spring in the figure has a spring constant of 1300 N/m. It is compressed 17.0 cm, then launches a 200 g block. The horizontal surface is frictionless, but the block’s coefficient of kinetic friction on the incline is 0.200. What distance d does the block sail through the air?arrow_forwardSolve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





