
Concept explainers
a)
To determine: System utilization rate.
Introduction: Poisson distribution is utilized to ascertain the probability of an occasion happening over a specific time period or interval. The interval can be one of time, zone, volume or separation. The probability of an event happening is discovered utilizing the equation in the Poisson distribution.
a)
Answer to Problem 17P
Explanation of Solution
Given Information:
It is given that the processing time is 4 customers per hour and there are 5 servers to process the customers.
| Class | Arrivals per Hour |
| 1 | 2 |
| 2 | 4 |
| 3 | 3 |
| 4 | 2 |
Calculate the system utilization:
It is calculated by adding all the total customer hours for each class and the result is divided with number of servers and customer process per hour.
Here,
M = number of servers
Hence the system utilization is 0.5500.
b)
To determine: The average customer waiting for service for each class and waiting in each class on average.
b)
Answer to Problem 17P
Explanation of Solution
Given Information:
| Class | Arrivals per Hour |
| 1 | 2 |
| 2 | 4 |
| 3 | 3 |
| 4 | 2 |
It is given that the processing time is 4 customers per hour and there are 5 servers to process the customers.
Calculate the average number of customers
It is calculated by dividing the total customers arrive per hour with customer process per hour.
Here,
r = average number of customers
Calculate average number of customers waiting for service (Lq) using infinite-source table values for
The Lq values for
Calculate A using Formula 18-16 from book:
It is calculated by subtracting 1 minus system utilization rate and multiplying the result with Lq, the whole result is divided by total customer arrival rate.
Here,
Lq = average number of customers waiting for service
Calculate B using Formula 18-17 from book for each category:
It is calculated by multiplying number of servers with customer service process rate per hour and the result is divided by total customer arrival rate for each category.
Here,
M = number of servers
Calculate the average waiting time for class 1 and class 2
It is calculated by multiplying A with B0 and B1, the result is divided by 1.
Calculate the average number of customers that are waiting for service for class 1 and class 2
It is calculated by multiplying total customer arrival rate with average waiting time for units in each category.
Excel Spreadsheet:

Excel Workings:
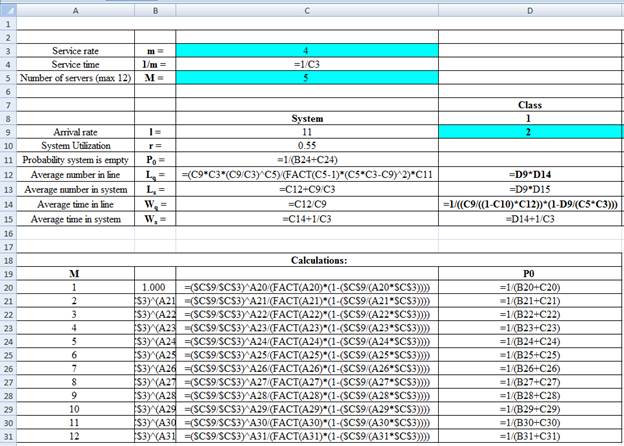
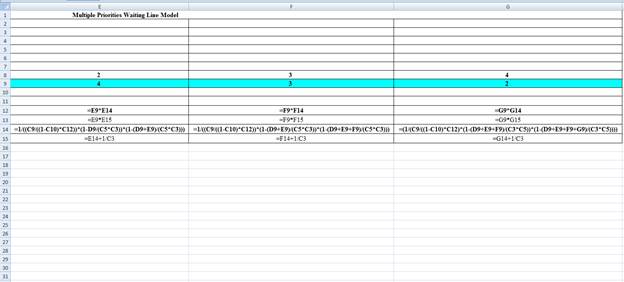
Hence the average wait time for service by customers for class 1 is 0.0099 hours, class 2 is 0.0142 hours, class 3 is 0.0232 hours and class 4 is 0.0361 hours. The waiting in each class on average for class 1 is 0.0199 customers, class 2 is 0.0567 customers, class 3 is 0.0696 customers and class 4 is 0.0722 customers.
c)
To determine: The average customer waiting for service for each class and waiting in each class on average.
c)
Answer to Problem 17P
Explanation of Solution
Given Information:
It is given that the processing time is 4 customers per hour and there are 5 servers to process the customers. The second priority class is reduced to 3 units per hour by shifting some into the third party class. The arrival rate is as follows,
| Class | Arrivals per Hour |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 2 |
Calculate the average number of customers
It is calculated by dividing the total customers arrive per hour with customer process per hour.
Here,
r = average number of customers
Calculate average number of customers waiting for service (Lq) using infinite-source table values for
The Lq values for
Calculate A using Formula 18-16 from book
It is calculated by subtracting 1 minus system utilization rate and multiplying the result with Lq, the whole result is divided by total customer arrival rate.
Here,
Lq = average number of customers waiting for service
Calculate B using Formula 18-17 from book for each category
It is calculated by multiplying number of servers with customer service process rate per hour and the result is divided by total customer arrival rate for each category.
Here,
M = number of servers
Calculate the average waiting time for class 1 and class 2
It is calculated by multiplying A with B0 and B1, the result is divided by 1.
Calculate the average number of customers that are waiting for service for class 1 and class 2
It is calculated by multiplying total customer arrival rate with average waiting time for units in each category.
Excel Spreadsheet:
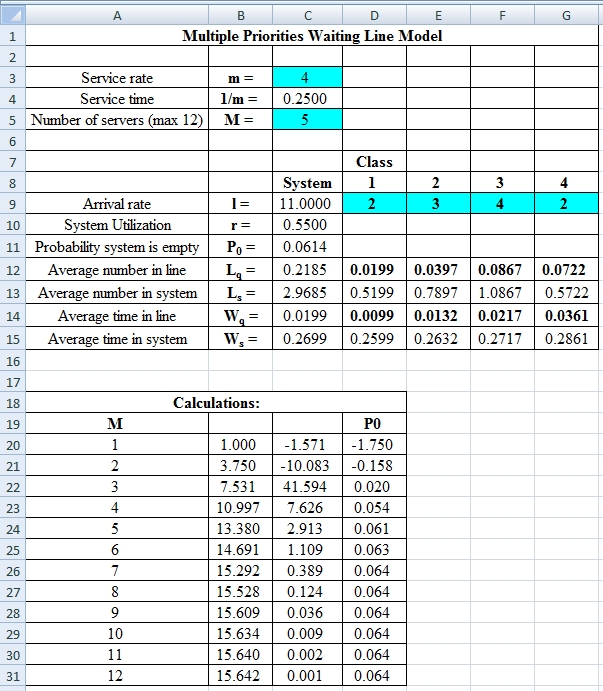
Excel Workings:
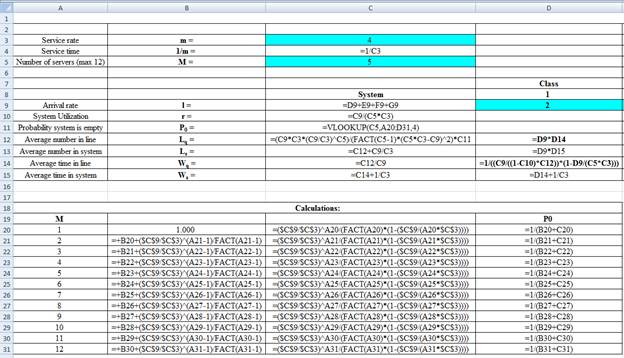
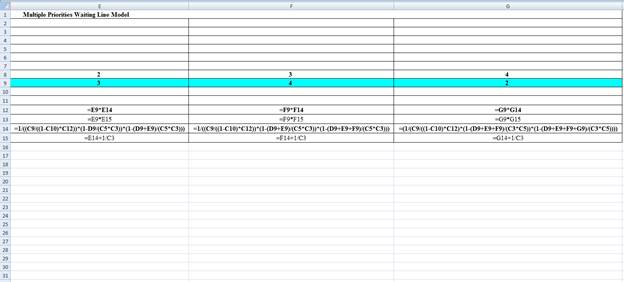
Hence the average wait time for service by customers for class 1 is 0.0099 hours, class 2 is 0.0132 hours, class 3 is 0.0217 hours and class 4 is 0.0361 hours. The waiting in each class on average for class 1 is 0.0199 customers, class 2 is 0.0397 customers, class 3 is 0.0867 customers and class 4 is 0.0722 customers.
d)
To determine: The observations based on the results from part c.
d)
Answer to Problem 17P
Explanation of Solution
Calculate the change in average wait time for each class.
It is calculated by subtracting the final answer for average wait time for service by customers from part b with the final answer for average wait time for service by customers from part c.
The above results suggest that there is a decrease in average wait time for class 2 and class 3. Class 1 and 4 remains constant.
Calculate the change in average number waiting for each class.
It is calculated by subtracting the final answer for waiting on average from part b with the final answer for waiting on average from part c.
The above results suggest that there is a decrease in average waiting for class 2 and an increase in class 3. Class 1 and 4 remains constant.
Want to see more full solutions like this?
Chapter 18 Solutions
EBK OPERATIONS MANAGEMENT
- Yellow Press, Inc., buys paper in 1,500-pound rolls for printing. Annual demand is 2,250 rolls. The cost per roll is $625, and the annual holding cost is 20 percent of the cost. Each order costs $75. a. How many rolls should Yellow Press order at a time? Yellow Press should order rolls at a time. (Enter your response rounded to the nearest whole number.)arrow_forwardPlease help with only the one I circled! I solved the others :)arrow_forwardOsprey Sports stocks everything that a musky fisherman could want in the Great North Woods. A particular musky lure has been very popular with local fishermen as well as those who buy lures on the Internet from Osprey Sports. The cost to place orders with the supplier is $40/order; the demand averages 3 lures per day, with a standard deviation of 1 lure; and the inventory holding cost is $1.00/lure/year. The lead time form the supplier is 10 days, with a standard deviation of 2 days. It is important to maintain a 97 percent cycle-service level to properly balance service with inventory holding costs. Osprey Sports is open 350 days a year to allow the owners the opportunity to fish for muskies during the prime season. The owners want to use a continuous review inventory system for this item. Refer to the standard normal table for z-values. a. What order quantity should be used? lures. (Enter your response rounded to the nearest whole number.)arrow_forward
- In a P system, the lead time for a box of weed-killer is two weeks and the review period is one week. Demand during the protection interval averages 262 boxes, with a standard deviation of demand during the protection interval of 40 boxes. a. What is the cycle-service level when the target inventory is set at 350 boxes? Refer to the standard normal table as needed. The cycle-service level is ☐ %. (Enter your response rounded to two decimal places.)arrow_forwardOakwood Hospital is considering using ABC analysis to classify laboratory SKUs into three categories: those that will be delivered daily from their supplier (Class A items), those that will be controlled using a continuous review system (B items), and those that will be held in a two bin system (C items). The following table shows the annual dollar usage for a sample of eight SKUs. Fill in the blanks for annual dollar usage below. (Enter your responses rounded to the mearest whole number.) Annual SKU Unit Value Demand (units) Dollar Usage 1 $1.50 200 2 $0.02 120,000 $ 3 $1.00 40,000 $ 4 $0.02 1,200 5 $4.50 700 6 $0.20 60,000 7 $0.90 350 8 $0.45 80arrow_forwardA part is produced in lots of 1,000 units. It is assembled from 2 components worth $30 total. The value added in production (for labor and variable overhead) is $30 per unit, bringing total costs per completed unit to $60 The average lead time for the part is 7 weeks and annual demand is 3800 units, based on 50 business weeks per year. Part 2 a. How many units of the part are held, on average, in cycle inventory? enter your response here unitsarrow_forward
- assume the initial inventory has no holding cost in the first period and back orders are not permitted. Allocating production capacity to meet demand at a minimum cost using the transportation method. What is the total cost? ENTER your response is a whole number (answer is not $17,000. That was INCORRECT)arrow_forwardRegular Period Time Overtime Supply Available puewag Subcontract Forecast 40 15 15 40 2 35 40 28 15 15 20 15 22 65 60 Initial inventory Regular-time cost per unit Overtime cost per unit Subcontract cost per unit 20 units $100 $150 $200 Carrying cost per unit per month 84arrow_forwardassume that the initial inventory has no holding cost in the first period, and back orders are not permitted. Allocating production capacity to meet demand at a minimum cost using the transportation method. The total cost is? (enter as whole number)arrow_forward
- The S&OP team at Kansas Furniture, led by David Angelow, has received estimates of demand requirements as shown in the table. Assuming one-time stockout costs for lost sales of $125 per unit, inventory carrying costs of $30 per unit per month, and zero beginning and ending inventory, evaluate the following plan on an incremental cost basis: Plan B: Vary the workforce to produce the prior month's demand. Demand was 1,300 units in June. The cost of hiring additional workers is $35 per unit produced. The cost of layoffs is $60 per unit cut back. (Enter all responses as whole numbers.) Note: Both hiring and layoff costs are incurred in the month of the change (i.e., going from production of 1,300 in July to 1300 in August requires a layoff (and related costs) of 0 units in August). Hire Month 1 July Demand 1300 Production (Units) Layoff (Units) Ending Inventory Stockouts (Units) 2 August 1150 3 September 1100 4 October 1600 5 November 1900 6 December 1900arrow_forwardThe S&OP team at Kansas Furniture, led by David Angelow, has received estimates of demand requirements as shown in the table. Assuming one-time stockout costs for lost sales of $100 per unit, inventory carrying costs of $20 per unit per month, and zero beginning and ending inventory, evaluate the following plan on an incremental cost basis: Plan A: Produce at a steady rate (equal to minimum requirements) of 1,100 units per month and subcontract additional units at a $65 per unit premium cost. Subcontracting capacity is limited to 800 units per month. (Enter all responses as whole numbers). Ending Month Demand Production Inventory Subcontract (Units) 1 July 1300 1,100 0 2 August 1150 1,100 0 3 September 1100 1,100 0 4 October 1600 1,100 0 5 November 1900 1,100 0 6 December 1200 1,100 0arrow_forwardPlease help me expand upon my research even more in detail please. Need help added more to mine from the photos please. Not sure what more I can add.arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing


