
Concept explainers
A 1.8-kg collar A and a 0.7-kg collar B can slide without friction on a frame, consisting of the horizontal rod OE and the vertical rod CD, which is free to rotate about its vertical axis of symmetry. The two collars are connected by a cord running over a pulley that is attached to the frame at O. At the instant shown, the velocity vA of collar A has a magnitude of 2.1 m/s and a stop prevents collar B from moving. The stop is suddenly removed and collar A moves toward E. As it reaches a distance of 0.12 m from O, the magnitude of its velocity is observed to be 2.5 m/s. Determine at that instant the magnitude of the angular velocity of the frame and the moment of inertia of the frame and pulley system about CD.
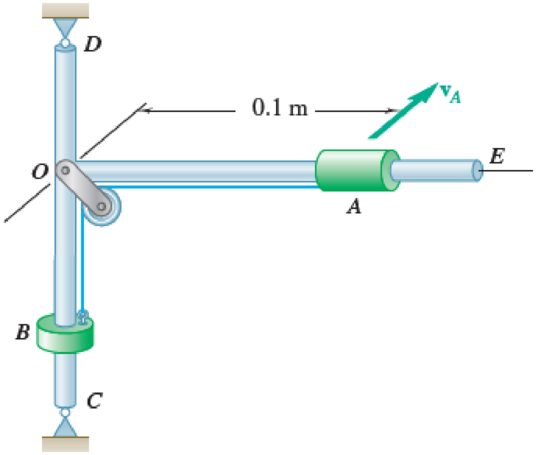
Fig. P17.89
Find the magnitude of the angular velocity of the frame and the moment of inertia of the frame and pulley system about CD.
Answer to Problem 17.89P
The magnitude of the angular velocity of the frame is
The magnitude of the moment of inertia of the frame and pulley system about CD is
Explanation of Solution
Given information:
The mass
The mass
The velocity
The distance
The velocity
Calculation:
Write the equation of the velocity component
Here,
Write the equation of the velocity
Here,
Let
Let
Write the equation of the velocity component
Substitute
Find the angular velocity
Substitute
The velocity of the collar A in radial direction at initial position
Find the equation of the kinetic energy
Here, I is the moment of inertia of the frame,
Substitute
At initial position, potential energy will be zero. Therefore,
Write the equation of the angular momentum
Substitute
Let
Write the equation of the velocity
Here,
Substitute 0.12 m for
Find the equation of the velocity component
Substitute
Find the velocity
Find the change in radial direction or constraint in collar A
Substitute 0.12 m for
Find the constraint in collar B using Equation (2).
Substitute
Find the equation of the kinetic energy
Substitute 1.8 kg for
Find the potential energy
Substitute 0.7 kg for
Find the angular momentum at final position
Substitute 1.8 kg for
Consider the conservation of angular momentum.
Substitute
Take
Consider the conservation of energy.
Substitute
Substitute
Substitute
Solve equation (4),
Thus, the magnitude of the moment of inertia of the frame and pulley system about CD
Find the magnitude of the angular velocity of the frame
Substitute
Thus, the magnitude of the angular velocity of the frame is
Want to see more full solutions like this?
Chapter 17 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
Additional Engineering Textbook Solutions
Thermodynamics: An Engineering Approach
Mechanics of Materials (10th Edition)
Problem Solving with C++ (10th Edition)
Starting Out With Visual Basic (8th Edition)
Fluid Mechanics: Fundamentals and Applications
- Figure below shows a link mechanism in which the link OA rotates uniformly in an anticlockwise direction at 10 rad/s. the lengths of the various links are OA=75 mm, OB-150 mm, BC=150 mm, CD-300 mm. Determine for the position shown, the sliding velocity of D. A 45 B Space Diagram o NTS (Not-to-Scale) C Darrow_forwardmotion is as follows; 1- Dwell 45°. Plot the displacement diagram for a cam with flat follower of width 14 mm. The required 2- Rising 60 mm in 90° with Simple Harmonic Motion. 3- Dwell 90°. 4- Falling 60 mm for 90° with Simple Harmonic Motion. 5- Dwell 45°. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm.arrow_forwardAn ideal gas, occupying a volume of 0.02 m3 , has a temperature of 25 0C and is at 1.2 bar. The gas is compressed reversibly and adiabatically to a final pressure of 8 bar. Assuming the gas has an adiabatic index of γ = 1.4, calculate (a) the final temperature, (b) the final volume, (c) the work performed during the compression and (d) the heat transferred.arrow_forward
- attached is a past paper question in which we werent given the solution. a solution with clear steps and justification would be massively appreciated thankyou.arrow_forwardin this scenario, when it comes to matrix iterations it states this system is assumed out of phase. why is this?arrow_forwardQ1. A curved beam of a circular cross section of diameter "d" is fixed at one end and subjected to a concentrated load P at the free end (Fig. 1). Calculate stresses at points A and C. Given: P = 800 N, d = 30 mm, a 25 mm, and b = 15 mm. Fig.1 P b B (10 Marks)arrow_forward
- You are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (p = 0.001 kg m-1 s-1) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be y = +h I 2h = 1 cm x1 y = -h u(y) 1 dP 2μ dx -y² + Ay + B moving plate stationary plate U 2 I2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page.arrow_forwardQuestion 1 You are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (µ = 0.001 kg m¯¹ s¯¹) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be 1 dP u(y) = 2μ dx -y² + Ay + B y= +h Ꮖ 2h=1 cm 1 x1 y = −h moving plate stationary plate 2 X2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page. (a) By considering the appropriate boundary conditions, show that the constants take the following forms: U U 1 dP A =…arrow_forwardQuestion 2 You are an engineer working in the propulsion team for a supersonic civil transport aircraft driven by a turbojet engine, where you have oversight of the design for the engine intake and the exhaust nozzle, indicated in Figure Q2a. The turbojet engine can operate when provided with air flow in the Mach number range, 0.60 to 0.80. You are asked to analyse a condition where the aircraft is flying at 472 m/s at an altitude of 14,000 m. For all parts of the question, you can assume that the flow path of air through the engine has a circular cross section. (a) ← intake normal shock 472 m/s A B (b) 50 m/s H 472 m/s B engine altitude: 14,000 m exhaust nozzle E F exit to atmosphere diameter: DE = 0.30 m E F diameter: DF = 0.66 m Figure Q2: Propulsion system for a supersonic aircraft. a) When the aircraft is at an altitude of 14,000 m, use the International Standard Atmosphere in the Module Data Book to state the local air pressure and tempera- ture. Thus show that the aircraft speed…arrow_forward
- يكا - put 96** I need a detailed drawing with explanation or in wake, and the top edge of im below the free surface of the water. Determine the hydrothed if hydrostatic on the Plot the displacement diagram for a cam with roller follower of diameter 10 mm. The required motion is as follows; 1- Rising 60 mm in 135° with uniform acceleration and retardation motion. 2- Dwell 90° 3- Falling 60 mm for 135° with Uniform acceleration-retardation motion. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm. =--20125 7357 750 X 2.01arrow_forwardYou are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (µ = 0.001 kg m¯¹ s¯¹) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be U y = +h У 2h = 1 cm 1 x1 y=-h u(y) = 1 dP 2μ dx -y² + Ay + B moving plate - U stationary plate 2 I2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page. (a) By considering the appropriate boundary conditions, show that the constants take the following forms: A = U 2h U 1 dP…arrow_forwardQuestion 2 You are an engineer working in the propulsion team for a supersonic civil transport aircraft driven by a turbojet engine, where you have oversight of the design for the engine intake and the exhaust nozzle, indicated in Figure Q2a. The turbojet engine can operate when provided with air flow in the Mach number range, 0.60 to 0.80. You are asked to analyse a condition where the aircraft is flying at 472 m/s at an altitude of 14,000 m. For all parts of the question, you can assume that the flow path of air through the engine has a circular cross section. (a) normal shock 472 m/s A B (b) intake engine altitude: 14,000 m D exhaust nozzle→ exit to atmosphere 472 m/s 50 m/s B diameter: DE = 0.30 m EX diameter: DF = 0.66 m Figure Q2: Propulsion system for a supersonic aircraft. F a) When the aircraft is at an altitude of 14,000 m, use the International Standard Atmosphere in the Module Data Book to state the local air pressure and tempera- ture. Thus show that the aircraft speed of…arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





