
Concept explainers
a.
To plot: The
Given information:
The atmospheric concentration of carbon dioxide (in parts per million) recorded by the observatory in years between 1960 and 2015.
| x | y |
| 1960 | 317 |
| 1970 | 326 |
| 1980 | 339 |
| 1990 | 354 |
| 2000 | 369 |
| 2005 | 380 |
| 2010 | 390 |
| 2015 | 401 |
Plot:
Take the year as x coordinate and concentration as y coordinate, and then draw the scatter plot as shown below:
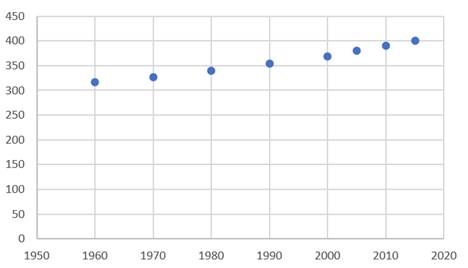
Interpretation:
From the scatter plot it seems that the linear regression will best fit the scenario.
b.
To find: If a linear or a quadratic model fit more appropriate.
A linear model seems more appropriate for the scatter plot.
Given information:
The atmospheric concentration of carbon dioxide (in parts per million) recorded by the observatory in years between 1960 and 2015.
| x | y |
| 1960 | 317 |
| 1970 | 326 |
| 1980 | 339 |
| 1990 | 354 |
| 2000 | 369 |
| 2005 | 380 |
| 2010 | 390 |
| 2015 | 401 |
Calculation:
Observe that the points do not fall nearly along a well-known curve. But, they do seem to fall near a line with upward slope.
Since the curve drawn seems to be a straight line, a linear model seems more appropriate for the scatter plot.
c.
To find: Find the regression equation for the appropriate model, and superimpose the graph of the regression equation on the scatter plot.
The regression can line by written as
Given information:
The atmospheric concentration of carbon dioxide (in parts per million) recorded by the observatory in years between 1960 and 2015.
| x | y |
| 1960 | 317 |
| 1970 | 326 |
| 1980 | 339 |
| 1990 | 354 |
| 2000 | 369 |
| 2005 | 380 |
| 2010 | 390 |
| 2015 | 401 |
Calculation:
Prepare the table to find the regression coefficients as follows;
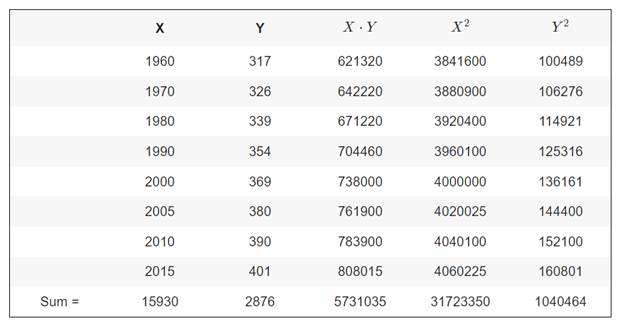
Use the table to perform the calculations as shown below.
Then,
Therefore,
So, the regression can line by written as
Now, plot the regression line as shown below.
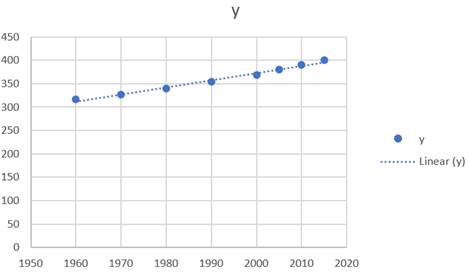
The graph of the regression line best fit the data. That means, the graph shows that the model appears to work well.
d.
To find: The approximate concentration level of carbon dioxide in the year 2025.
The concentration of carbon dioxide in the year 2025 will be
Given information:
The atmospheric concentration of carbon dioxide (in parts per million) recorded by the observatory in years between 1960 and 2015.
| x | y |
| 1960 | 317 |
| 1970 | 326 |
| 1980 | 339 |
| 1990 | 354 |
| 2000 | 369 |
| 2005 | 380 |
| 2010 | 390 |
| 2015 | 401 |
Calculation:
The model for the given situation is
Substitute
Conclusion:
The concentration of carbon dioxide in the year 2025 will be
e.
To explain: The circumstances that might caused the predication in part (d) of the mark and tell whether the true value will be higher or lower than the predicted value.
Given information:
The atmospheric concentration of carbon dioxide (in parts per million) recorded by the observatory in years between 1960 and 2015.
| x | y |
| 1960 | 317 |
| 1970 | 326 |
| 1980 | 339 |
| 1990 | 354 |
| 2000 | 369 |
| 2005 | 380 |
| 2010 | 390 |
| 2015 | 401 |
Explanation:
If the model is predicted to be an upward quadratic, then the prediction in part (d) would have been off the mark.
Since an upward quadratic function gives a higher value than a linear function with upward slope, the true value would have been lower than the predicated value.
Chapter 1 Solutions
PRECALCULUS:GRAPHICAL,...-W/ACCESS
- This table displays the current in equal intervals. Time t/ms 05 10 15 20 25 30 Current i/A 0 4.8 9.1 12.7 8.8 3.5 0 The formula for the charge as follows: 30x10-3 q 0 i dt Use formula to solve the current at 30ms using both the trapezoidal rule and Simpson's rule showing all steps and workingarrow_forwardTable displays the current in equal intervals. Charge formula: Time t/m 05 10 15 20 25 30 Current i/A 0 4.8 9.1 12.7 8.8 3.5 0 9 = 70 30x10-3 i dt Using mid-ordinate rule solve for the current at 30ms.arrow_forwardEvaluate 5 k=0 7 2. karrow_forward
- Pls help asap pls.arrow_forward9. Consider the function y = 2e¯*. Determine the equation of the tangent(s) to the curve that pass through the point P(2, 0). Your final answer must be expressed in standard form as per other tests. Negative exponents and/or fractions must not appear in your final answer. For full marks please draw an accurate sketch to support your solution.arrow_forward6. The graph below shows f, f'and fƒ" Clearly Label the curves.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





